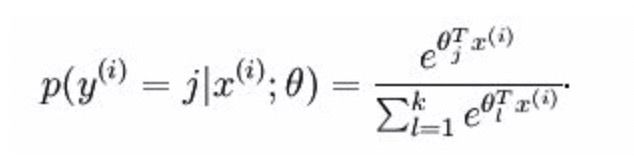图上的机器学习系列-聊聊DeepWalk

前言

本篇着重结合论文《DeepWalk: Online Learning of Social Representations》来聊，过程中尽量把一些概念和方法展开多讨论一下。

DeepWalk是干啥的

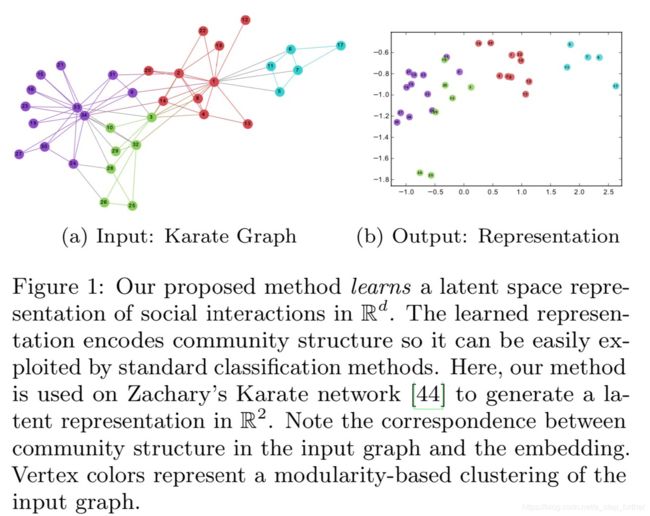
我们来想这样一件事：机器学习是咋工作的？需要输入一堆特征变量对吧？无论是离散型还是连续型，但都是欧式空间中的数学表达，总归是可以用很多数学工具来分析的。但一个社交网络的图结构呢？每一个点该如何进行数学表达，才能在上面开展一些模型训练？于是有一帮聪明人就想到了：可以把图上的每一个节点也表示成一个数学向量啊！ 于是，就诞生了Graph Embedding这样一个领域，它研究的就是用向量来表示图上的节点，且保留了这样一个重要的性质：在图上距离较近的节点，在向量空间中的距离也较近。下图这个例子可以帮助我们理解这个过程：

等等，这种感觉是不是似曾相似？SVM、感知机等这些方法也是把一个原本我们hold不住的数据，经过某种神奇的变换（要么是投影到某一个平面、线上，要么是降到一个更低维的空间中，要么是做出各种数学变换），总之吧，就是把一个未知的、不好搞定的问题，转化为一个已知的、好搞定的问题上来。

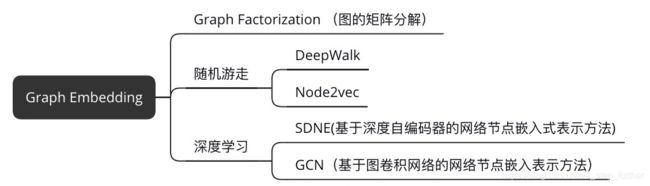
又啰嗦了，拐回来继续说DeepWalk。既然说它是一类Graph Embedding方法，那么一定还有其它的方法对吧？参考网上的资料整理方法如下图所示：

参考资料[1]是一篇Graph Embedding的文献综述，感兴趣的读者可以找来看看。

理解DeepWalk

那么，DeepWalk是怎样实现这个向量化的表达呢？我们不妨来推演一下这里的思路，以下是笔者脑补的思考过程：

随机游走

首先是得想办法生成训练数据，也就是上述的随机游走了。这个过程相对还容易理解，论文中作者是这样表述的：

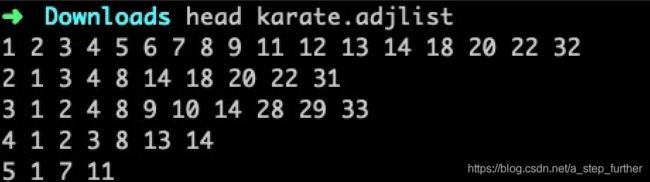
但是，不动手写写代码，老是有一种不踏实的感觉，有没有？那我们就找份数据实操一下。玩过网络分析的朋友对Karate Graph想必都非常熟悉（也即前文第一部分的案例图），源数据可以从github上获得（https://github.com/phanein/deepwalk/blob/master/example_graphs/karate.adjlist）

这个文件格式的每一行表示首列节点ID的邻居节点列表：

如果自己不动手画出来这个网络看上一眼，也觉得不踏实，那就画呗，用networkx也就是几行代码的事儿：

现在就想想如果是自己来实现这个随机游走过程，该怎么写呗。于是一边听京剧，一边开始了我的土代码：

import random
walks = []
nodes = list(G.nodes)
r = 10  # 每个节点产生r个序列
t = 5   # 每个序列的长度
for i in range(0,r):
    for v in nodes:
        cur_walk = [v]
        for step in range(0,t-1):
            cur_v = cur_walk[-1]
            neighbours = list(G.adj[cur_v])
            # 随机选择一个邻居
            rc_nei = random.choice(neighbours)
            cur_walk.append(rc_nei)
        walks.append(cur_walk)
            
print("共计得到%d个序列" % len(walks))

SkipGram

SkipGram 是应用于Word2Vec的方法之一，它的本质是一个浅层的神经网络模型（只有一个隐藏层）。参考资料[4]讲述SkipGram非常详细，推荐找来看看。下面两张图浓缩了其方法的精华。

为什么留下隐藏层的权重就是我们想要的向量表示了呢？
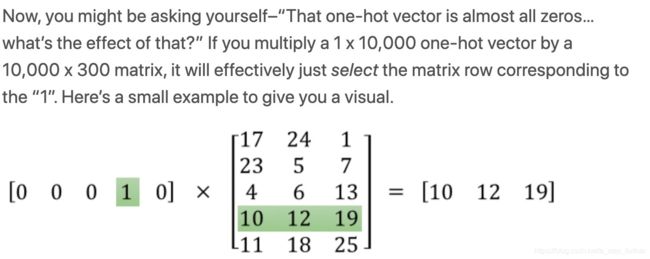
注意到输出层使用的是Softmax分类器，它其实就是多分类场景下logistic回归方法的扩展，而我们知道logistic回归在二分类时的决策平面其实是一个线性平面，那么猜想softmax的决策平面也是线性的。说明经过中间隐藏层的转换后，输入的不同样本点在新的空间中生成的数据点集是可以通过线性平面来分割的，同类之间距离比较小，不同类之间距离较大。这不恰好也与Graph Embedding的初心相吻合嘛！而输入的样本是经过one-hot-encoding编码的，乘以隐藏层的权重矩阵，其实就是取到了其中某一行而已，所以说这一行也就相当于样本点在新空间中的坐标向量，正如下面的案例所示意的那样：

于是乎，我们知道了怎样将图结构转化为类似于文本的样本格式，然后再去训练一个神经网络，提炼出隐藏层的权重向量，就实现我们的目标了。

等一下，回头再看一眼论文给的伪代码描述，总感觉哪里还是没聊到。

这里为什么要把节点集合变成一棵二叉树呢？作者的论述如下图所示：

但是，我仍然没有看懂。。。（每当这时就会暴露出非CS专业毕业弱鸡的软肋）
查了一些资料才了解到，原来这个Hierarchical Softmax是Facebook做的一个文本分类算法（FastText）中使用到的降低计算量（从隐藏层到输出层）的技巧，也就是说，我们前面知道输出层的神经元使用的是softmax分类器，输出值是一个概率值，而该概率值的计算方法如下，为了归一化，每一个类别都参与计算一次，这个计算量就比较大了。

Hierarchical Softmax优化点在于，它构造了一棵Huffman树，每一个叶子节点代表一个图节点或者单词，想计算它出现的条件概率，在对应的分支路径上把数值（每一个分裂节点使用了一个logistic二分类回归，所以产出了分到左支和右支的概率值）依次累乘即可，显著减少了计算量。

再来说为啥每一轮迭代时，对节点做了一个shuffle。论文中作者是这样说的：

This is not strictly required, but is well-known to speed up the convergence of stochastic gradient descent.

“well-known”…又一次感受到了“无知”的自卑感。好吧，我个人的定性理解是这样的：随机梯度下降的方法要求每次随机抽取一条样本来参与训练，而我们在遍历节点时，第一轮进行完，到第二轮时，如果还是以同样的节点顺序来遍历，那么样本的出现就具有了一定的规律，不够“随机”了，所以要对节点做一次随机排序，以加强样本顺序的随机性。

 

小结

DeepWalk借鉴了Word2Vec中SkipGram的方法，利用一个浅层的神经网络来进行有监督训练，最终得到隐藏层的向量矩阵即为所求向量化表达。过程中涉及到了图结构转换为节点序列，使用了随机游走的方法。总体上该方法比较简洁易懂，也因此成为了一种比较经典的图嵌入方法。细节上的讨论出于笔者个人理解，如有谬误，欢迎留言指正与讨论。

 

参考资料

1. Goyal P , Ferrara E . Graph Embedding Techniques, Applications, and Performance: A Survey[J]. Knowledge-Based Systems, 2017.
2. Perozzi B, Al-Rfou R, Skiena S. DeepWalk: Online Learning of Social Representations[C]// Acm Sigkdd International Conference on Knowledge Discovery & Data Mining. 2014.
3. [https://networkx.github.io/documentation/networkx-1.2/reference/index.html]
4. http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/
5. http://www.perozzi.net/
6. https://developer.alipay.com/article/6513

 

欢迎关注本人公众号：