人工智能：深度学习算法及应用——简单理解CNN卷积神经网络并python实现（带源码）

简单理解CNN卷积神经网络的原理及其使用
本文使用的代码链接：
链接：pan.baidu.com/s/1JAKwNl3FCOecyfllfDckHA
提取码：r47h
链接2：pan.baidu.com/s/1b4mj5MFwCBj1npKH5SGiJA?pwd=yqbh
提取码：yqbh

一、 实验目的

1. 了解深度学习的基本原理
2. 能够使用深度学习开源工具识别图像中的数字
3. 了解图像识别的基本原理

二、 实验要求

1. 解释深度学习原理；
2. 对实验性能进行分析；
3. 回答思考题；

三、 实验的硬件、软件平台

硬件：计算机
软件：操作系统：WINDOWS
　　 应用软件：Tensorflow-gpu、Python、NumPy、PyCharm、CUDA

四、 实验原理

1.1. 深度学习概述

深度学习归根结底也是机器学习的一种，如果说要做机器学习分类的话，除了分成监督学习、无监督学习、半监督学习和增强学习之外，从算法网络深度的角度来看还可以分成浅层学习算法和深度学习算法。

1.2. 深度学习的常见结构

常见结构有DNN,CNN,RNN。DNN是表示有深度学习网络的算法的统称，CNN主要是一种空间概念上的深度学习结构，RNN是时间概念上的深度学习结构。
深度神经网络（DNN）：
DNN泛指多层次的神经网络，这些模型的隐藏层之间彼此相连。只是针对处理数据的种类和特点不同，衍生出各种不同的结构，如CNN和RNN。

1.3. 卷积神经网络（CNN）

想要识别图像中的物体，就需要提取出比较好的特征，该特征应能很好地描述想要识别的物体。所以物体的特征提取是一项非常重要的工作。而图像中物体的特征以下几种特点：

如以上图中狗的鼻子特征：
① 物体的特征可能只占图像中的一小部分。比如下图中狗的鼻子只是图像中很小的一部分。
② 同样的特征可能出现在不同图像中的不同位置，比如下图中狗的鼻子在两幅图中出现的位置不同。
③ 缩放图像的大小对物体特征的影响可能不大，比如下图是缩小后的图，但依然能很清楚的辨认出狗的鼻子。

而卷积神经网络中的卷积与池化操作能够较好地抓住物体特征的以上 3 种特点。

卷积

卷积说白了就是有一个卷积核(其实就是一个带权值的滑动窗口)在图像上从左到右，从上到下地扫描，每次扫描的时候都会将卷积核里的值所构成的矩阵与图像被卷积核覆盖的像素值矩阵做内积。整个过程如下图所示，其中黄色方框代表卷积核，绿色部分代表单通道图像，红色部分代表卷积计算后的结果，通常称为特征图：

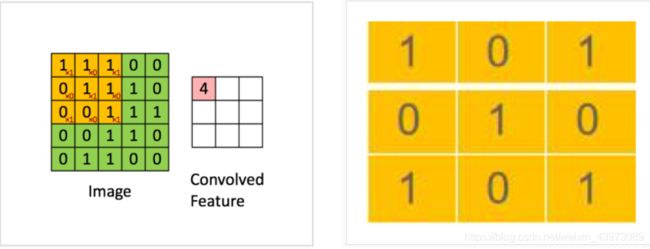
**那为什么说卷积能够提取图像中物体的特征呢？**其实很好理解，上图中的卷积核中值的分布如上右图；
当这个卷积核卷积的时候就会在3行3列的小范围内计算出图像中几乎所有的 3 行 3 列子图像与卷积核的相似程度（也就是内积的计算结果）。相似程度越高说明该区域中的像素值与卷积核越相似。(上图的特征图中值为 4 的位置所对应到的源图像子区域中像素值的分布与卷积核值的分布最为接近)这也就说明了卷积在提取特征时能够考虑到特征可能只占图像的一小部分，以及同样的特征可能出现在不同的图像中不同的位置这两个特点。卷积核的值很明显是训练出来的！

对于一个图像，可以经过不止一个卷积核的卷积，得到多个特征图，特征图的个数与卷积核的个数相等。
当然，上述的卷积核仅仅是一个最简单的卷积核，除此之外，还有扩张卷积：包含一个叫做扩张率的参数，定义了卷积核内参数间的行（列）间隔数，或者又如转置卷积。
对于要处理的二维图像而言，其不仅有长和宽两个变量，还有一个称为“通道”的变量，如上述的例子，输入的图像可表示为(4, 4, 1)，表示长和宽都是4，有1个通道，经过N个上述的 3 x 3 卷积核后，其可以变成(2, 2, N)，即有了N个通道。在这里，可以把其看作是N个二维的图像组合而成的一个三维图像。
对于多通道的图像，假定其有N个通道，经过一个 3 x 3 的卷积核，那么这个卷积核也应该为(3, 3, N)，使用这一个卷积核对每一个通道相同的位置进行卷积，得到了N个值，将这N个值求和，作为输出图像中的一个值。所以，得到的通道的数目只与卷积核的个数有关。

池化

从上面卷积层可以看到，我们的目的是对一个图像进行特征提取，最终得到了一个N通道的图像，但是，如果卷积核的数量太多，那么得到的特征图数量也是非常多。这时就需要池化层来降低卷积层输出的特征维度，同时可以防止过拟合现象。
由于图像具有一种“静态性”的属性，也就是在一个图像区域有用的特征极有可能在另一个区域同样有用，所以通过池化层可以来降低图像的维度。
这里只介绍我使用的一般池化的方法。一般池化包括平均池化和最大池化两种。

池化就是将输入图像进行缩小，减少像素信息，只保留重要信息。 池化的操作也很简单，通常情况下，池化区域是 2 行 2 列的大小，然后按一定规则转换成相应的值，例如最常用的最大池化( max pooling )。最大池化保留了每一小块内的最大值，也就是相当于保留了这一块最佳的匹配结果。举个例子，如下图中图像是 4 行 4 列的，池化区域是 2 行 2 列的，所以最终池化后的特征图是 2 行 2 列的。图像中粉色区域最大的值是 6 ，所以池化后特征图中粉色位置的值是 6 ，图像中绿色区域最大的值是 8 ，所以池化后特征图中绿色位置的值是 8 ，以此类推。

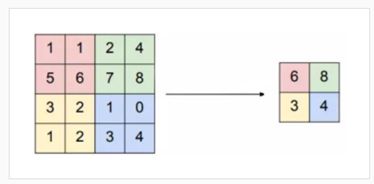
从上图可以看出，最大池化不仅仅缩小了图像的大小，减少后续卷积的计算量，而且保留了最佳的特征（如果图像是经过卷积后的特征图）。也就相当于把图缩小了，但主要特征还在，这就考虑到了缩放图像的大小对物体的特征影响可能不大的特点。

全连接网络

卷积与池化能够很好的提取图像中物体的特征，当提取好特征之后就可以着手开始使用全连接网络来进行分类了。全连接网络的大致结构如下：

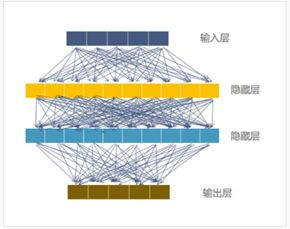
其中输入层通常指的是对图像进行卷积，池化等计算之后并进行扁平后的特征图。隐藏层中每个方块代表一个神经元，每一个神经元可以看成是一个很简单的线性分类器和激活函数的组合。输出层中神经元的数量一般为标签类别的数量，激活函数为 softmax （因为将该图像是猫或者狗的得分进行概率化）。因此我们可以讲全连接网络理解成很多个简单的分类器的组合，来构建成一个非常强大的分类器。

1.4. 卷积神经网络的大致结构

将卷积，池化，全连接网络进行合理的组合，就能构建出属于自己的神经网络来识别图像中数字。通常来说卷积，池化可以多叠加几层用来提取特征，然后接上一个全连接网络来进行分类。大致结构如下：

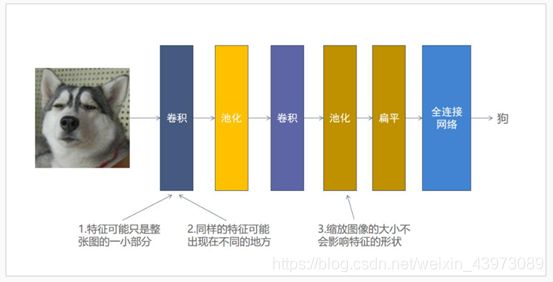
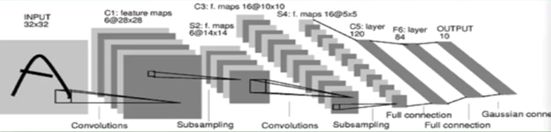
1.5. 参数学习

CNN的学习也是和神经网络一样，先经过前向传播，得到当前的预测值，再计算误差，将误差反向传播，更新全连接层的权值和卷积核的参数。这里存在一个问题，如果卷积核的参数都不同，那么需要更新的参数数量会非常多。为了解决这个问题，采用了参数共享的机制，即对于每一个卷积核，其对每个通道而言权值都是相同的。

和全连接神经网络相比，卷积神经网络的训练要复杂一些。但训练的原理是一样的：利用链式求导计算损失函数对每个权重的偏导数（梯度），然后根据梯度下降公式更新权重。训练算法依然是反向传播算法。
卷积神经网络的三个思路：

• 局部连接
  这个是最容易想到的，每个神经元不再和上一层的所有神经元相连，而只和一小部分神经元相连。这样就减少了很多参数。
• 权值共享
  一组连接可以共享同一个权重，而不是每个连接有一个不同的权重，这样又减少了很多参数。
• 下采样
  可以使用Pooling来减少每层的样本数，进一步减少参数数量，同时还可以提升模型的鲁棒性。

对于图像识别任务来说，卷积神经网络通过尽可能保留重要的参数，去掉大量不重要的参数，来达到更好的学习效果。

五、 实验内容与步骤

1. 深度学习工具安装

安装开源深度学习工具设计并实现一个深度学习模型，它能够学习识别图像中的数字序列。然后使用数据训练它：你可以使用人工合成的数据（推荐），或直接使用现实数据。

这里我直接使用PyCharm Community Edition 2020.2.1（方便好用）平台作为载体；

1.1. 使用pip命令安装tensorflow-gpu 1.9.0

这里为了能够使用GPU加速运行，需要下载安装gpu版本的tensorflow；
需要注意的是python3.8并不提供tensorflow2.2以下版本，需要安装python3.6或python3.5版本。

1.2. 下载安装CUDA Toolkit 9.0

CUDA(Compute Unified Device Architecture)，显卡厂商NVidia推出的运算平台。 CUDA™是一种由NVIDIA推出的通用并行计算bai架构，该架构使GPU能够解决复杂的计算问题。 它包含了CUDA指令集架构(ISA)以及GPU内部的并行计算引擎。

随着显卡的发展，GPU越来越强大，而且GPU为显示图像做了优化。在计算上已经超越了通用的CPU。如此强大的芯片如果只是作为显卡就太浪费了，因此NVidia推出CUDA，让显卡可以用于图像计算以外的目的。

1.3. 下载cuDDN7.1.4

NVIDIA cuDNN是用于深度神经网络的GPU加速库。它强调性能、易用性和低内存开销。NVIDIA cuDNN可以集成到更高级别的机器学习框架中，如加州大学伯克利分校的流行CAFFE软件。简单的，插入式设计可以让开发人员专注于设计和实现神经网络模型，而不是调整性能，同时还可以在GPU上实现高性能现代并行计算。

CuDNN支持的算法：
①卷积操作、相关操作的前向和后向过程。
②pooling的前向后向过程
③softmax的前向后向过程
④激活函数的前向后向过程（ReLU、sigmoid、TANH）
⑤Tensor转换函数，其中一个Tensor就是一个四维的向量。

这里需要将下载好的CuDNN的内容加入到下载安装好的CUDA中即可。

1.4. 环境配置
当上述的软件安装完成后检查是否安装成功，同时在系统环境中进行配置。

注：CUDA、cuDNN、python、tensorflow-gpu的版本都是必须要适配的，刚开始不怎么懂导致版本不匹配出现很多错误，走了不少弯路。

2. 认识数据
   这里使用的数据为 MNIST 数据集种的数字。 MNIST 数据库是由 Yann 提供的手写数字数据库文件。这个数据库主要包含了 55000 张的训练图像和 10000 张的测试图像。其中部分数据可视化如下图所示：
   
   MNIST是机器学习领域的一个经典问题，指的是让机器查看一系列大小为28x28像素的手写数字灰度图像，并判断这些图像代表0-9中的哪一个数字。每个数字由2828的像素组成。
   使用python代码下载MINST数据集，并保存在指定路径下：
   
   但是有可能出现url无法访问的错误，这时候可以手动下载官网的mnist_dataset包放在目录下。
   测试图片的存储形式与结构：
   
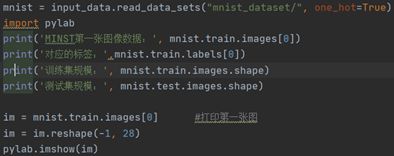
   测试MNIST图像数据与规模如下：
   
   
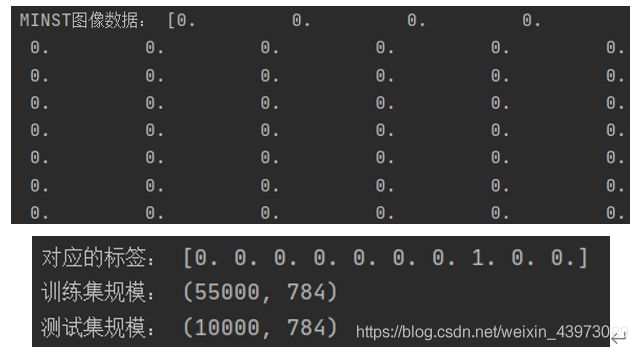
   可以看出图片2828像素使用数组存储，第一个数字图片为3；
   对应的标签为一维向量，标签则占用10位，我们可以将标签看作为一个数组，其中，正常情况下，数组中的每个元素都是0，只有当某一位为1的时候，它的下标，就是代表了图片中的数字，比如如果第三位为1（下标为2），且其他九位全部为0，那么，说明这张图片里面存放的手写数字是3。；

3. CNN设计

• 输入图片大小为2828，卷积层步幅为1，采样窗口为55，采用SAME PADDING（卷积不改变图片大小）；池化层步幅为2，采样窗口为2*2，采用最大池化；

• 该网络一共有两个卷积层，两个池化层，两个全连接层。
  卷积层1深度为32，即32个卷积核从1个平面抽取特征；卷积层2深度为64，即64个卷积核从32个平面抽取特征；池化层2输出后来到全连接层1，有512个神经元，之后是全连接层2，也是输出层，有10个神经元。具体顺序如下：
  
  以一张图片为例：
  

• 使用截断正态分布初始化权值，标准差为0.1
  一般来讲权重矩阵是K个N维向量。从直觉上来讲，如果这K个N维向量在N维空间中均匀分布在以原点为中心的N-1维单位超球面上，在随机性上应该是最好的。因为这样，这K个向量的夹角为均匀分布。此时问题变成了，如何在N-1维超球面上进行均匀采样。
  若对N维向量的每个分量进行N(0,1)的正态分布采样，生成K个N维向量，然后投影到单位超球面上，那么形成的K个N维向量在单位超球面上均匀分布。所以用正态分布初始化，再单位化，就可以达到这种效果。当然也可以不必单位化。

• 将偏置初始化为常量0.1

• 采用交叉熵（cross-entropy）损失代价函数
  

• 交叉熵代价函数：
  
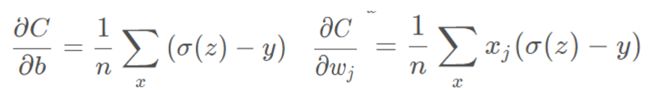
  其中C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本总数。
  可以看出，权值和偏置值的调整与σ ′ ( z )无关。**另外，梯度公式中的σ ( z ) − y 表示输出值与实际值的误差。**所以当误差越大时，梯度就越大，参数W和b 的调整就越快，训练的速度也就越快。

• 采用dropout，随机丢弃掉一半的神经元

• 做完卷积后采用ReLU激活函数，函数的定义是：f ( x ) = m a x ( 0 , x )

Relu函数作为激活函数，有下面三个优势：
速度快
和sigmoid函数需要计算指数和倒数相比，relu函数其实就是一个max(0,x)，计算代价 小很多。
减轻梯度消失问题
回忆一下计算梯度的公式∇ = σ ′ δ 。其中，σ ′ 是sigmoid函数的导数。在使用反向传 播算法进行梯度计算时，每经过一层sigmoid神经元，梯度就要乘上一个σ ′ 。从下图 可以看出，σ ′函数最大值是1/4。因此，乘一个σ ′ 会导致梯度越来越小，这对于深层网 络的训练是个很大的问题。而relu函数的导数是1，不会导致梯度变小。当然，激活函 数仅仅是导致梯度减小的一个因素，但无论如何在这方面relu的表现强于sigmoid。使 用relu激活函数可以训练更深的网络。
稀疏性
通过对大脑的研究发现，大脑在工作的时候只有大约5%的神经元是激活的，而采用 sigmoid激活函数的人工神经网络，其激活率大约是50%。有论文声称人工神经网络在 15%-30%的激活率时是比较理想的。因为relu函数在输入小于0时是完全不激活的，因 此可以获得一个更低的激活率。

• 分类器使用softmax函数
  Softmax回归模型是logistic回归模型在多分类问题上的推广，当分类数为2的时候会退化为Logistic分类。.在多分类问题中，类标签y可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的，是有监督的。

4. 具体实现

① 首先，读入数据；

之前已经通过了代码下载好了MINST数据集，这里将其对应的文件位置作为路径，即可实现MINST数据集导入到算法中的操作，这里使用了一个input_data函数，有两个参数，第一个是数据集的路径，第二个是one_hot标记位。
这个one_hot标记位，表示将样本标签转化为one hot编码，这个编码的意思是：假如所有的编码一共有10类（0——9的10个数字），0的one hot就是1000000000；

②设置batch的大小为100，同时处理100张图片作为输入；

③ 声明了占位符（向量）

None代表该向量的第一个维度是可以为任意长度的，因此，利用占位符X就能够保存所有任意数量的MINST图像（这里是55000张）；第二维度为784，即28的平方，代表每张图片所含有的784个像素点。
Y占位符则是保存每一张图片对应的标签，同样适用None匹配任意数量的数据集，且第二维度长度限定为10，代表与10个数字相对应。

tf.placeholder(dtype, shape=None, name=None)
此函数可以理解为形参，用于定义过程，在执行的时候再赋具体的值
dtype：数据类型。常用的是tf.float32,tf.float64等数值类型
shape：数据形状。默认是None，就是一维值，也可以是多维，比如[2,3], [None, 3]表示列是3，行不定
name：名称。
赋值一般用sess.run(feed_dict = {x:xs, y_:ys})，其中x,y_是用placeholder创建出来的

④CNN网络建立

第一层卷积，卷积核定义为5x5,1是输入的通道数目，32是输出的通道数目，每个输出通道对应一个偏置，经过卷积运算之后，并使用ReLu激活函数激活。

第一层池化，这里用到的是一个22的池化，通过了22的池化，之后的图片规模变成了14*14。
注意到，在输入到池化层之前需要经过Relu函数进行激活，这就是前向传播过程的一部分实现。

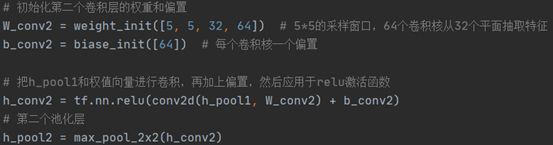
第二个卷积层与池化层，与第一个卷积层稍微不同，采用了64个卷积核，将生成64张卷积特征图，深度将变为64；

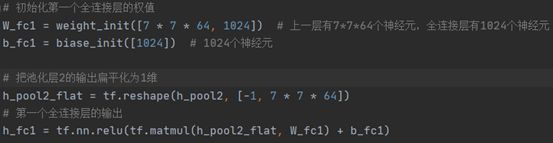
初始化一个全连接层，因为第二个池化层结束之后图片尺寸减小到7x7，我们加入一个有1024个神经元的全连接层，用于处理整个图片，加上对应的偏置和展开数据，并最后再次使用relu激活函数。

为了防止过拟合，在全连接层和输出层之间定义了一个dropout，让一定数目的神经元（百分比）没有输出。
同时定义一个全连接层用于分类。

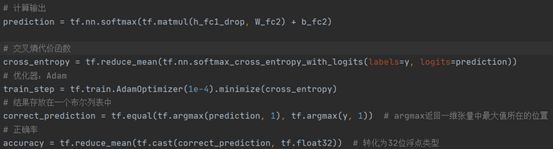
该部分主要用于定义输出函数（通过softmax函数进行）、代价（交叉熵）计算、代价优化器（Adam）、结果的保存、正确率的计算；

最后，主要的学习过程如下：

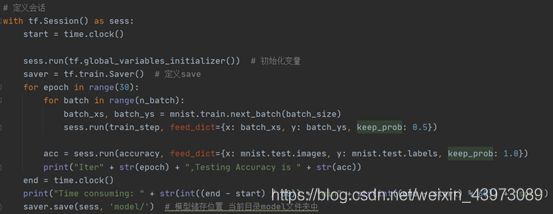
为了防止过拟合，在构建神经网络的时候定义了一个dropout，它的功能是让一定百分比的神经元没有输出。在前一句run中，那是一个训练过程，为了防止过拟合，因此dropout定义为0.5，即50%的神经元没有输出。第二句run用于检测模型的准确率，出于准确的考虑，dropout应该为1.0，即神经元都有输出，尽可能得到正确的答案。

最后将学习好的模型存储在model文件夹中。

5. 学习结果分析

• 迭代过程中的准确率更新如图所示（共迭代了30次，前面的学习过程）；
  
  
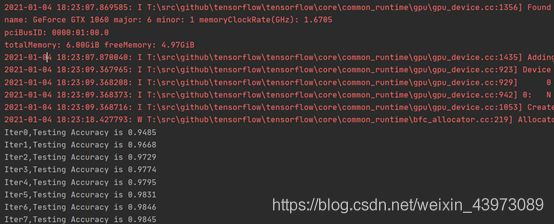
  可以看到，这里是使用了GPU来进行加速的，说明前面的安装过程最终是成功了！
  这里通过30次迭代，我们的准确率稳定在了99.2%左右，并且在不断地波动，识别正确率是很不错的，这里我还用了50次迭代来测试，发现其实准确率可以达到99.3%以上。

• 此外，通过加载学习好的模型进行数字识别的测试，主要代码如下，其余的深度学习网络结构与训练过程中的一致。
  
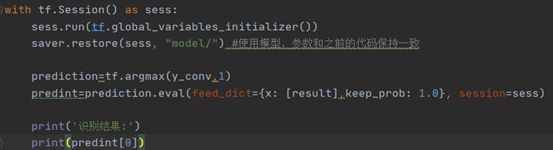
  首先，分析我们的模型存储文件；
  ① Meta graph:
  这是一个保存完整Tensorflow graph的protocol buffer，比如说，所有的 variables, operations, collections等等。这个文件的后缀是 .meta 。
  
  ② Checkpoint file:
  这是一个包含所有权重（weights），偏置（biases），梯度（gradients）和所有其他保存的变量（variables）的二进制文件。它包含两个文件：
  mymodel.data-00000-of-00001、mymodel.index
  其中，.data文件包含了我们的训练变量。另外，除了这两个文件，Tensorflow有一个叫做checkpoint的文件，记录着已经最新的保存的模型文件。
  接着，进行图片识别测试：
  
  可以看到，都是可以正确识别的。

六、 思考

1. 深度算法参数的设置对算法性能的影响？

在我具体实现的过程中，有如下发现：

• batch（每一批的大小），学习率，迭代次数，dropout的keep_prob大小都会影响算法的性能；
• batch为50时比其他条件相同时batch为100效果要稍微好一些；
• 学习率大了收敛速度快，但是会有抖动现象，学习率小了收敛速度又很慢；
• 未收敛之前，错误率随着迭代次数的增加而减小，但越到后面越趋于稳定，所以迭代次数并不是越多越好，还要考虑时间耗费；
• dropout小于1时，会增加模型训练的时间，但是一定程度上可以解决过拟合的问题；
• 选择不同的权重和偏置初始化方法也会对算法性能造成影响；
• 选择不同的代价函数也会对算法性能造成影响，比如本次实验选择交叉熵代价函数就优于二次代价函数；
• 选择不同的优化器同样会对算法性能造成影响，比如本次实验选择Adam优化器就略优于GradientDescent优化器。

2. 为什么用CNN（卷积神经网络）？

我们的任务是图像识别，而CNN相较于全连接神经网络有更明显的优点，比DNN更加适合于图像处理。
全连接神经网络之所以不太适合图像识别任务，主要有以下几个方面的问题：

• 参数数量太多
  考虑一个输入10001000像素的图片(一百万像素，现在已经不能算大图了)，输入层有10001000=100万节点。假设第一个隐藏层有100个节点(这个数量并不多)，那么仅这一层就有(1000*1000+1)*100=1亿参数，这实在是太多了！我们看到图像只扩大一点，参数数量就会多很多，因此它的扩展性很差。
• 没有利用像素之间的位置信息
  对于图像识别任务来说，每个像素和其周围像素的联系是比较紧密的，和离得很远的像素的联系可能就很小了。如果一个神经元和上一层所有神经元相连，那么就相当于对于一个像素来说，把图像的所有像素都等同看待，这不符合前面的假设。当我们完成每个连接权重的学习之后，最终可能会发现，有大量的权重，它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重，这样的学习必将是非常低效的。
• 网络层数限制
  我们知道网络层数越多其表达能力越强，但是通过梯度下降方法训练深度全连接神经网络很困难，因为全连接神经网络的梯度很难传递超过3层。因此，我们不可能得到一个很深的全连接神经网络，也就限制了它的能力。
  而CNN就可以很好的解决上面的问题。

七、 实验总结

本次实验主要是深度学习的数字图像识别，具体来说涉及到了很多东西，包括数字图像的表示形式、CNN卷积神经网络的基础知识和优点等等。
说实话深度学习这一方面我们的课程是完全没有提到的，所有的东西都要自己学，所以刚开始只能先去看深度学习的介绍，CNN的介绍和相关概念的阐述，稍微理解之后就去看数字识别的一些代码实战，我看的最多的并不是MNIST集的而是验证码的识别，然后加深印象后再慢慢的看学长们的博客，慢慢的去理解CNN。卷积神经网络非常的精妙，它非常的适合于图片识别的学习，因为图片的像素往往是非常多的，而CNN又非常简单的可以进行特征的提取，使得要处理的数据逐渐变小而又可以保持原来的特征。
当然，整个实验过程中最令我觉得开心的还是实现了GPU的加速。刚开始用CPU来跑发现非常的慢，CPU占用率很高，几乎没办法在跑数据的时候来使用电脑做其他事，效率很低。而使用GPU加速的话以后跑数据可以快上不少的同时不占用CPU。
这门课的实验到这里就结束了，总的来说课外扩展的东西比较多，真正的在书上详细涉及到的也就只有实验一了，不过这样也算是可以学习到更多的知识和技能，获益匪浅。