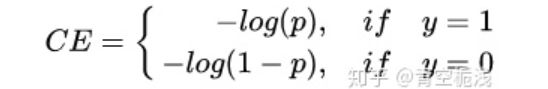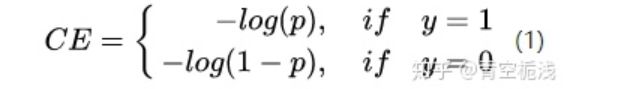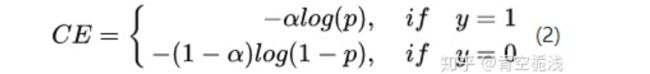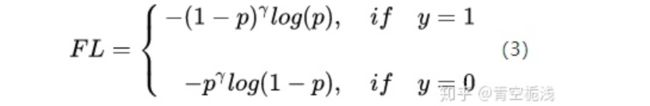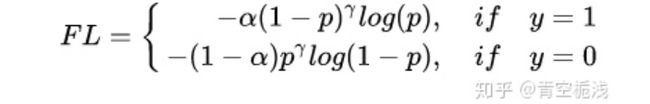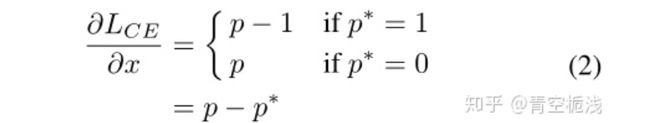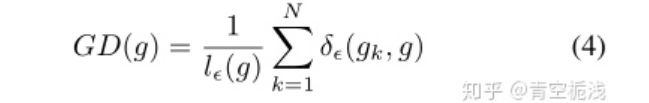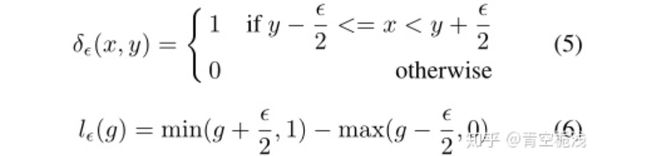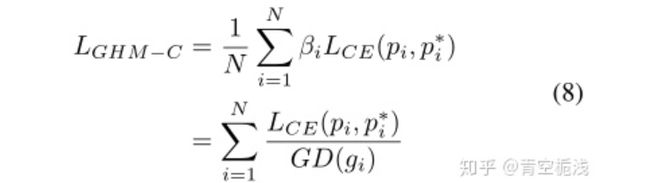NLP样本不均衡之常用损失函数对比（附代码）

本文分为三个部分，第一个部分主要介绍一下在分类问题中为什么用交叉熵作为损失函数，第二部分主要介绍一下在交叉熵的基础上的一些改进的损失函数，最后使用上述的几种损失函数在 CLUENER 细粒度命名实体识别的数据集上进行效果的效果对比。

作者：青空栀浅

地址：https://www.zhihu.com/people/yangning9371

编辑：人工智能前沿讲习

01

为什么使用交叉熵作为损失函数？

交叉熵作为最常用的损失函数想必再熟悉不过了，本节简单介绍一下交叉熵作为loss的优势。

1.1 为什么不用classification error？

下面通过两个例子来说明一下：

假设下面为两个模型的结果，其中predict为模型的预测值，target为真实的分类。

model_1:

model_2:

通过上面两个表的对比，可以看出模型2的效果要明显优于模型1，因为在正确的分类上模型的预测结果都显著大于其他类别。但是从classification error上发现两个模型的效果是一样的，发现问题了吧，classification error不能准确的描述模型与理想的模型的距离。

1.2 为什么不用Mean Squared Error

model_1:

model_2:

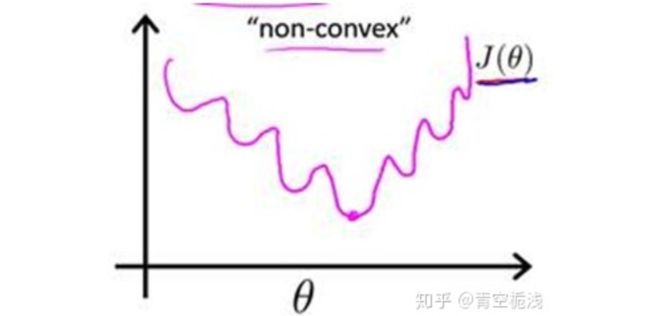
MSE 看起来也不错，不用它的原因是因为：

如果用 MSE 计算 loss， 其损失函数是一个非凸函数，存在很多局部极值点并且MSE更容易导致梯度弥散。

关于这个问题，已经有很多回答了，这里就不展开说了。

1.3 使用交叉熵的损失

model_1:

model_2:

cross-entropy 更清晰的描述了模型与理想模型的距离,并且CE作为loss其也是一个凸函数。

02

交叉熵的基础上的一些改进的损失函数

2.1 Label Smoothing

在这个公式中，  表示  的标准交叉熵损失函数，  是一个非常小的正数，  表示对应的正确分类，  为所有分类的数量。

直观上看，标记平滑限制了正确类的  值，并使得它更接近于其他类的  值。从而在一定程度上，它被当作为一种正则化技术和一种对抗模型过度自信的方法。

2.2 Focal Loss

Focal Loss的引入主要是为了解决难易样本数量不平衡（注意，有区别于正负样本数量不平衡）的问题，这里将样本分为四个类型

我们在计算分类的时候常用的损失——交叉熵的公式如下：

为了解决正负样本不平衡的问题，我们通常会在交叉熵损失的前面加上一个参数  ，即：

尽管  平衡了正负样本，但对难易样本的不平衡没有任何帮助。因为易分样本虽然损失很低，但是数量太多，导致最终主导了损失。而作者认为，易分样本（即，置信度高的样本）对模型的提升效果非常小，模型应该主要关注与那些难分样本（这个假设是有问题的，是GHM的主要改进对象）。一个简单的思想：把高置信度(p)样本的损失再降低一些不就好了，即：

举个例子  ，如果  ,那么  ，损失衰减了1000倍！

Focal Loss的最终形式如下：

即结合了（2）和（3）式，简单明了。

2.3 GHM_C

GHM_C是在Focal的基础上的进一步改进，首先看一下Focal存在的问题：

• 首先，让模型过度关注特别难分的样本其实是有问题的，因为那种样本点很可能本身就是离群点或者是标注错误等造成的样本。

• 其次，Focal中的  与  是根据实验得出来的，并且 与 的值也会相互影响，不同数据需要不断尝试调整 与 。

研究者对样本不均衡的本质影响进行了进一步探讨，找到了梯度分布这个更为深入的角度。认为样本不均衡的本质是分布的不均衡。更进一步来看，每个样本对模型训练的实质作用是产生一个梯度用以更新模型的参数，不同样本对参数更新会产生不同的贡献。由于简单样本的数量非常大，它们产生的累计贡献就在模型更新中就会有巨大的影响力甚至占据主导作用，而由于它们本身已经被模型很好的判别，所以这部分的参数更新并不会改善模型的判断能力，也就使整个训练变得低效。

基于这一点，研究者对样本梯度的分布进行了统计，并根据这个分布设计了一个梯度均衡机制，使得模型训练更加高效与稳健，并可以收敛到更好的结果。

首先定义一个统计对象——梯度模长（gradient norm）。考虑简单的二分类交叉熵损失函数：

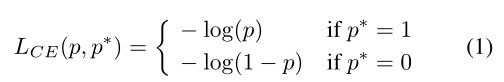
其中  为模型所预测的样本类别的概率，  是真实类别[0,1]。则其对  的梯度（导数）为：

于是定义梯度模长，g:

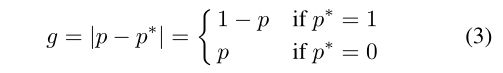
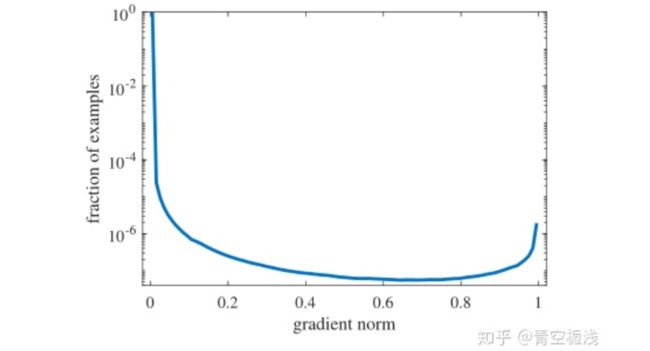
下图为论文中展示的梯度模长与样本量的关系，可以看出绝大部分的样本集中于梯度模长较小的区域内（图中左侧），也就是所谓的易分样本。

那怎么同时衰减易分样本和特别难分的样本呢?太简单了，谁的数量多衰减谁呗！那怎么衰减数量多的呢？简单啊，定义一个变量，让这个变量能衡量出一定梯度范围内的样本数量——这不就是物理上密度的概念吗？

接下来定义梯度密度：

于是，作者定义了梯度密度  ——本文最重要的公式：

其中：

 就是在样本N中，梯度模长分布在  范围内的样本数。  代表了  的区间长度。

因此梯度密度的物理含义是：单位梯度模长g部分的样本个数。

接下来梯度均衡的参数定义为：

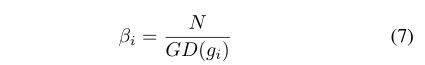
其中的  就是所有的样本数。

最终GHM_C的定义形式就是：

接下来看一下该损失函数的效果：

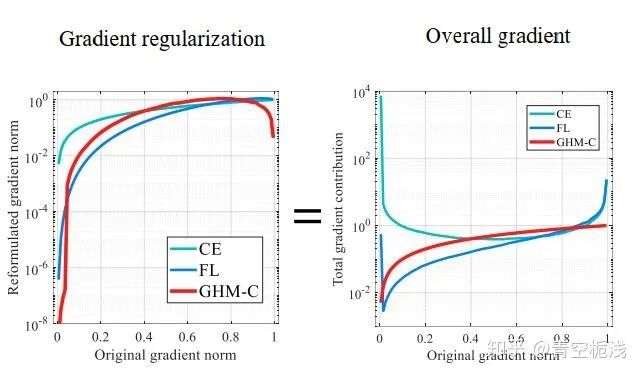
左边的图的意思就是不同损失函数对样本梯度产生的作用，横坐标为在交叉熵（CE）损失函数下样本的梯度模长，纵坐标为新的损失函数下同样的样本新的梯度模长，可以看出FL作为损失函数的情况下对于易分样本的确是存在抑制作用的，GHM-C作为损失函数不仅对易分样本有抑制，并且对特别难分的样本也是存在抑制作用的。右图中也可以看出GHM_C在易分样本上有相对的抑制，对于其他样本的梯度较为均衡。

03

不同损失函数的评测

在 CLUENER 细粒度命名实体识别的数据集上对上文提到的损失函数进行效果的对比。

因为命名实体识别的的模型相对于其他模型的数据样本就是很不平衡的。

数据集：

数据集地址：

https://www.cluebenchmarks.com/introduce.html

训练集：10748
验证集集：1343


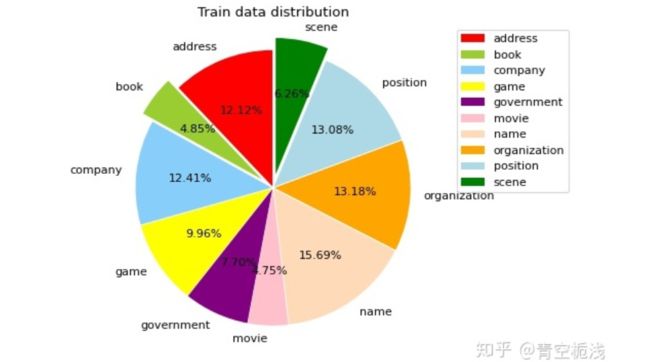
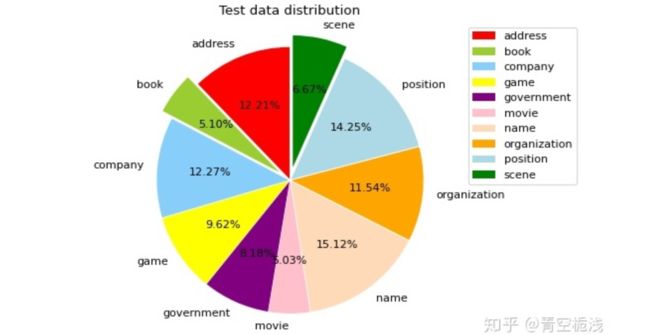
按照不同标签类别统计，训练集数据分布如下（注：一条数据中出现的所有实体都进行标注，如果一条数据出现两个地址（address）实体，那么统计地址（address）类别数据的时候，算两条数据）：
【训练集】标签数据分布如下：
地址（address）:2829
书名（book）:1131
公司（company）:2897
游戏（game）:2325
政府（government）:1797
电影（movie）:1109
姓名（name）:3661
组织机构（organization）:3075
职位（position）:3052
景点（scene）:1462


【验证集】标签数据分布如下：
地址（address）:364
书名（book）:152
公司（company）:366
游戏（game）:287
政府（government）:244
电影（movie）:150
姓名（name）:451
组织机构（organization）:344
职位（position）:425
景点（scene）:199


以train.json为例，数据分为两列：text & label，其中text列代表文本，label列代表文本中出现的所有包含在10个类别中的实体。
例如：
  text: "北京勘察设计协会副会长兼秘书长周荫如"
  label: {"organization": {"北京勘察设计协会": [[0, 7]]}, "name": {"周荫如": [[15, 17]]}, "position": {"副会长": [[8, 10]], "秘书长": [[12, 14]]}}
  其中，organization，name，position代表实体类别，
  "organization": {"北京勘察设计协会": [[0, 7]]}：表示原text中，"北京勘察设计协会" 是类别为 "组织机构（organization）" 的实体, 并且start_index为0，end_index为7 （注：下标从0开始计数）
  "name": {"周荫如": [[15, 17]]}：表示原text中，"周荫如" 是类别为 "姓名（name）" 的实体, 并且start_index为15，end_index为17
  "position": {"副会长": [[8, 10]], "秘书长": [[12, 14]]}：表示原text中，"副会长" 是类别为 "职位（position）" 的实体, 并且start_index为8，end_index为10，同时，"秘书长" 也是类别为 "职位（position）" 的实体,
  并且start_index为12，end_index为14

各标签分布如下：

在10种类型中，book,movie,scene的占比相对较少。

模型：

模型使用的是Bert+two_pointer的方式，即预测实体的start-position和end-position的方式。

这种形式下构建的数据集的标签也是很不均衡的。例如：

{"text": "《艺术与投资》：对你来说是一个水到渠成的事情？", 
"label": {"book": {"《艺术与投资》": [[0, 6]]}}}


start_tag:2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
end_tag:  0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

可以看出其实大部分的标签是0，就是非实体的意思。

使用该模型对以上的四种损失函数的测试结果如下：

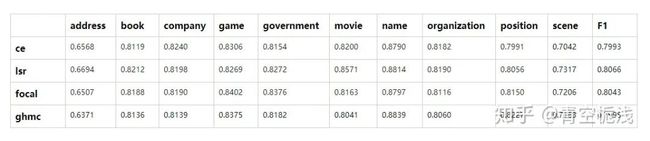
表格中前几列为各个标签的F1值，最后一列为总体的F1值。

下图为四种损失函数的变化趋势：

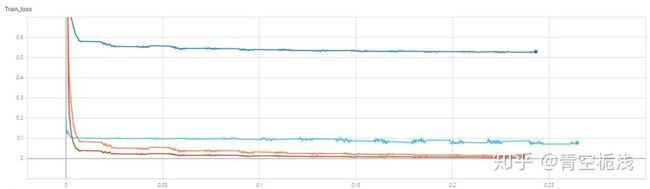
从loss曲线来看，四个损失函数下模型已经收敛，从F1效果看整体的效果是：

lsr的效果最好，其次是focal，然后是ghmc最后是ce。

也可以看出四个损失函数下其实模型的差距并不显著。

相关代码已经上传，详见我的github:

https://github.com/qingkongzhiqian/NER_loss_compare

04

ToDo:

目前只是测试四种损失函数在 CLUENER 细粒度命名实体识别的数据集上的效果，还没有统计该数据集的梯度模长的分布，后续添加吧！

05

总结

本文首先介绍了为什么用交叉熵作为损失函数，然后介绍了一些常用的损失函数，最后使用上述的几种损失函数在 CLUENER 细粒度命名实体识别的数据集上进行效果的效果对比。

06

参考

https://zhuanlan.zhihu.com/p/80594704

https://zhuanlan.zhihu.com/p/80594704

https://github.com/CLUEbenchmark/CLUENER2020

https://www.cnblogs.com/maybe2030/p/9163479.html

本文目的在于学术交流，并不代表本公众号赞同其观点或对其内容真实性负责，版权归原作者所有，如有侵权请告知删除。

下载一：中文版！学习TensorFlow、PyTorch、机器学习、深度学习和数据结构五件套！

后台回复【五件套】
下载二：南大模式识别PPT

后台回复【南大模式识别】

说个正事哈

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方“深度学习自然语言处理”，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

投稿或交流学习，备注：昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多：机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦

推荐两个专辑给大家：

专辑 | 李宏毅人类语言处理2020笔记

专辑 | NLP论文解读

专辑 | 情感分析

整理不易，还望给个在看！