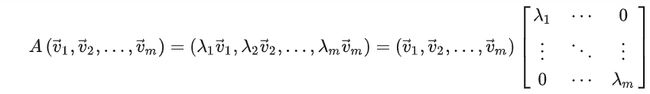四、视觉SLAM所需基本知识——矩阵论

  在视觉SLAM中需要用到很多的矩阵知识，例如超定方程的求解、SVD分解、QR分解等，这些概念对于理解SLAM的求解过程还是很重要的，因此下面对SLAM中需要用到的一些矩阵知识做一下回顾和整理。

①矩阵的秩和行列式

  一个矩阵表达了对一个向量的变换，这个变换可能包括平移、旋转、拉伸等等，矩阵的一些性质表达了这个变换的一些性质。

  矩阵的秩分为行秩和列秩，分别表示了线性无关的行向量或者列向量的个数，秩表达了一个矩阵所张开空间的维数，秩在一定程度上体现了矩阵包含实际信息的能力。

  行列式的值表达了尺度的缩放程度。

②方程求解

  参考链接：

https://zhuanlan.zhihu.com/p/423850164

https://www.cnblogs.com/samaritan-z/p/8432227.html

https://zhuanlan.zhihu.com/p/413247298

③特征分解

  矩阵的乘法本质上是对向量做变换，在变换的过程中，可能会遇到不改变向量的方向只改变向量的长度的情况，这种情况下该向量的方向是一个特殊的方向，被称为特征向量，对长度的缩放系数被称为特征值，特征值与特征向量用公式描述的话为：$Ax=\lambda x$，其中$x$为特征向量，$\lambda$为特征值。该式子无法完备的表示矩阵$A$，对于一个秩为$m$的矩阵，应该要有$m$个这样的表达式：

  简写为$AV=V\Sigma$，那么就可以用$A=V\Sigma V^{-1}$来表示$A$，也就是完成了对矩阵$A$的分解。其中$V$为特征向量组成的矩阵，$\Sigma$为特征值组成的对角矩阵。

④SVD分解

  上述的特征分解要求矩阵为方阵，当矩阵不为方阵的时候可以使用SVD分解，假设待分解的矩阵$A$是一个$m\ast n$的矩阵，则可以定义矩阵的SVD分解为：$A=U\Sigma V^T$，其中$U$是一个$m\ast m$的矩阵，$\Sigma$是一个$m\ast n$的对角矩阵，主对角线上的元素被称为奇异值（非负特征值的算数平方根），$V$是一个$n\ast n$的矩阵，$U$和$V$都是正交矩阵。

⑤QR分解

  矩阵的QR分解指的是将矩阵分解为正交矩阵和上三角矩阵的乘积，该分解方法在解决最小二乘问题和特征值计算方面都十分重要。

  设$A$为$n$阶非奇异实（复）矩阵，则存在正交（酉）矩阵$Q$和非奇异实（复）上三角矩阵$R$满足$A=QR$。能进行QR分解的条件为$A$的各个列向量是线性无关的。

矩阵论使用示例

  上面介绍了一些矩阵相关的知识，下面通过一个例子来使用一下上述的知识，比较常见的就是超定方程的求解，假设一个超定方程$Ax=b$，当$b=0$是为齐次形式，当$b$不等于0时为非齐次形式（$x$为$n$维向量）。

  ①当为非齐次线性方程组时，是否有解析解取决于增广矩阵的秩。

若$r(A)=r(A|b)=n$，有唯一解；

若$r(A)=r(A|b)<n$，有无穷多解；

若$r(A)<r(A|b)$，无解，这时候只能求最小二乘近似解（$r(A)=n$）。

采用最小二乘法求解非齐次线性方程组，公式为$x=(A^{T}A{)}^{-1}{A}^{T}b$。

  ②当为齐次线性方程组时，是否有解析解取决于$A$的秩。

若$r(A)=n$，此时有且只有0解；

若$r(A)<n$，此时有无穷多组解；

若$r(A)=n$，且$m>n$，此时解析解也只有零解（方程数大于未知数个数），如果想要求解其非零解，只能通过最小二乘法近似求解。

  若采用最小二乘法求解其近似解，主要有两种办法，方法一是对矩阵做$SVD$分解，分解后$V$的最后一列为$Ax=0$的最小二乘解。方法二是求解$A^{T}A$的特征向量和特征值最小的特征值对应的特征向量为最小二乘解。