week 6 贪心

P1223 排队接水

排队接水

题目描述

有 $n$ 个人在一个水龙头前排队接水，假如每个人接水的时间为 $T_i$，请编程找出这 $n$ 个人排队的一种顺序，使得 $n$ 个人的平均等待时间最小。

输入格式

第一行为一个整数 $n$。

第二行 $n$ 个整数，第 $i$ 个整数 $T_i$ 表示第 $i$ 个人的等待时间 $T_i$。

输出格式

输出文件有两行，第一行为一种平均时间最短的排队顺序；第二行为这种排列方案下的平均等待时间（输出结果精确到小数点后两位）。

样例 #1

样例输入 #1

10 
56 12 1 99 1000 234 33 55 99 812

样例输出 #1

3 2 7 8 1 4 9 6 10 5
291.90

提示

$n\le 1000,t_i\le 10^6$，不保证 $t_i$ 不重复。

当 $t_i$ 重复时，按照输入顺序即可（sort 是可以的）

思路

由于若把时间长的放在后面接水，那么就较少人等，所以排序+贪心即可，对接水时间从小到大排序，这就是打水顺序，然后累加总的接水时间，最后求平均值

代码

#include
using namespace std;
int n;
double sum;
struct node{
	double t;
	int id;
}a[10000];
int cmp(node x,node y)
{
	if (x.t==y.t) return x.id<y.id;
	return x.t<y.t;
}
int main()
{
	cin>>n;
	for (int i=1;i<=n;i++) cin>>a[i].t,a[i].id=i;
	sort(a+1,a+1+n,cmp);
	for (int i=1;i<=n;i++) 
	{
		cout<<a[i].id<<" ";
		sum+=a[i].t*(n-i);
	}
	cout<<endl;
	double ans=sum/n;
	printf("%.2f",ans);
	return 0;
} 

P1007 独木桥

独木桥

题目背景

战争已经进入到紧要时间。你是运输小队长，正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激，于是命令你的士兵们到前方的一座独木桥上欣赏风景，而你留在桥下欣赏士兵们。士兵们十分愤怒，因为这座独木桥十分狭窄，只能容纳 $1$ 个人通过。假如有 $2$ 个人相向而行在桥上相遇，那么他们 $2$ 个人将无法绕过对方，只能有 $1$ 个人回头下桥，让另一个人先通过。但是，可以有多个人同时呆在同一个位置。

题目描述

突然，你收到从指挥部发来的信息，敌军的轰炸机正朝着你所在的独木桥飞来！为了安全，你的部队必须撤下独木桥。独木桥的长度为 $L$，士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 $1$，但一个士兵某一时刻来到了坐标为 $0$ 或 $L+1$ 的位置，他就离开了独木桥。

每个士兵都有一个初始面对的方向，他们会以匀速朝着这个方向行走，中途不会自己改变方向。但是，如果两个士兵面对面相遇，他们无法彼此通过对方，于是就分别转身，继续行走。转身不需要任何的时间。

由于先前的愤怒，你已不能控制你的士兵。甚至，你连每个士兵初始面对的方向都不知道。因此，你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外，总部也在安排阻拦敌人的进攻，因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。

输入格式

第一行共一个整数 $L$，表示独木桥的长度。桥上的坐标为 $1,2,\cdots ,L$。

第二行共一个整数 $N$，表示初始时留在桥上的士兵数目。

第三行共有 $N$ 个整数，分别表示每个士兵的初始坐标。

输出格式

共一行，输出 $2$ 个整数，分别表示部队撤离独木桥的最小时间和最大时间。$2$ 个整数由一个空格符分开。

样例 #1

样例输入 #1

4
2
1 3

样例输出 #1

2 4

提示

对于 $100\%$ 的数据，满足初始时，没有两个士兵同在一个坐标，$1\le L\le 5\times 10^3$，$0\le N\le 5\times 10^3$，且数据保证 $N\le L$。

思路

这题需要转换一下思路

两个人相遇转身，相当于交换灵魂后继续走

所以最大值就是最靠近端点两个人各自向对方走,时间较长的那个人的时间
最小值就是所有人中走完桥最小值中的最大值
这里“最小值中的最大值”需要着重理解一下，因为就算是找最小值，也得让所有人都能够走完，所以得在这之中求最大值

代码

#include
using namespace std;
int L,l,n,maxx,minn;
int main()
{
	cin>>L>>n;
	for (int i=1;i<=n;i++)
	{
		cin>>l;
		maxx=max(maxx,max(l,L-l+1));
		minn=max(minn,min(l,L-l+1));
	} 
	cout<<minn<<" "<<maxx<<endl;
	return 0;
}

P1199 [NOIP2010 普及组] 三国游戏

[NOIP2010 普及组] 三国游戏

题目描述

小涵很喜欢电脑游戏，这些天他正在玩一个叫做《三国》的游戏。

在游戏中，小涵和计算机各执一方，组建各自的军队进行对战。游戏中共有 $N$ 位武将（$N$为偶数且不小于$4$），任意两个武将之间有一个“默契值”，表示若此两位武将作为一对组合作战时，该组合的威力有多大。游戏开始前，所有武将都是自由的（称为自由武将，一旦某个自由武将被选中作为某方军队的一员，那么他就不再是自由武将了），换句话说，所谓的自由武将不属于任何一方。

游戏开始，小涵和计算机要从自由武将中挑选武将组成自己的军队，规则如下：小涵先从自由武将中选出一个加入自己的军队，然后计算机也从自由武将中选出一个加入计算机方的军队。接下来一直按照“小涵→计算机→小涵→……”的顺序选择武将，直到所有的武将被双方均分完。然后，程序自动从双方军队中各挑出一对默契值最高的武将组合代表自己的军队进行二对二比武，拥有更高默契值的一对武将组合获胜，表示两军交战，拥有获胜武将组合的一方获胜。

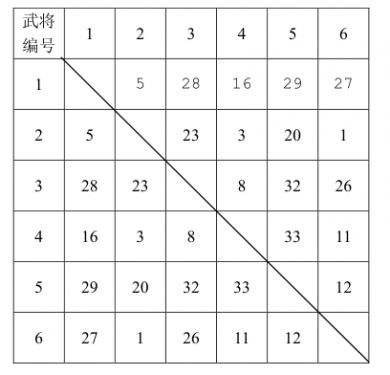
已知计算机一方选择武将的原则是尽量破坏对手下一步将形成的最强组合，它采取的具体策略如下：任何时刻，轮到计算机挑选时，它会尝试将对手军队中的每个武将与当前每个自由武将进行一一配对，找出所有配对中默契值最高的那对武将组合，并将该组合中的自由武将选入自己的军队。 下面举例说明计算机的选将策略，例如，游戏中一共有$6$个武将，他们相互之间的默契值如下表所示：

双方选将过程如下所示：

小涵想知道，如果计算机在一局游戏中始终坚持上面这个策略，那么自己有没有可能必胜？如果有，在所有可能的胜利结局中，自己那对用于比武的武将组合的默契值最大是多少？

假设整个游戏过程中，对战双方任何时候均能看到自由武将队中的武将和对方军队的武将。为了简化问题，保证对于不同的武将组合，其默契值均不相同。

输入格式

共 N 行。

第一行为一个偶数 $N$，表示武将的个数。

第 $2 $行到第 $N $行里，第$i+1$行有$N_i$个非负整数，每两个数之间用一个空格隔开，表示$ i $号武将和$ i+1,i+2,…,N $号武将之间的默契值（$0\le$默契值$\le 1,000,000,000$）。

输出格式

共 $1$ 或 $2 $行。

若对于给定的游戏输入，存在可以让小涵获胜的选将顺序，则输出$ 1$，并另起一行输出所有获胜的情况中，小涵最终选出的武将组合的最大默契值。如果不存在可以让小涵获胜的选将顺序，则输出 $0$。

样例 #1

样例输入 #1

6 
5 28 16 29 27 
23 3 20 1 
8 32 26 
33 11 
12

样例输出 #1

1
32

样例 #2

样例输入 #2

8 
42 24 10 29 27 12 58 
31 8 16 26 80 6 
25 3 36 11 5 
33 20 17 13 
15 77 9 
4 50 
19

样例输出 #2

1
77

提示

【数据范围】

对于$ 40%$的数据有 $N\le 10$。

对于$ 70%$的数据有$ N≤18$。

对于 $100\%$的数据有 $N\le 500$。

思路

博弈论，计算机拿走的武将都与小涵所拿走的武将的默契值最大所以小涵永远拿不到与自己所选武将默契值最高的武将。那么按照机器的策略，机器永远会选择第二大的。所以我们可以选择与A默契值第二大的武将，那么计算机只能选择小于这个默契值中最大的武将，所以小涵必赢

#include
using namespace std;
int n,a[510][510],ans;
int main()
{
	cin>>n;
	for (int i=1;i<=n-1;i++)
	  for (int j=i+1;j<=n;j++)
	  {
	  	cin>>a[i][j];
	  	a[j][i]=a[i][j];
	  }
	for (int i=1;i<=n;i++)
	{
		sort(a[i]+1,a[i]+1+n);//找出这一行中最大的那一个
		if (ans<a[i][n-1]) ans=a[i][n-1];//更新答案 
	}
	cout<<1<<endl<<ans<<endl;
	return 0;
}