【Learning Notes】Gumbel 分布及应用浅析
1. 分布的形式化
物理意义
Gumbel 分布是一种极值型分布。举例而言,假设每次测量心率值为一个随机变量(服从某种指数族分布,如正态分布),每天测量10次心率并取最大的一个心率值作为当天的心率测量值。显然,每天纪录的心率值也是一个随机变量,并且它的概率分布即为 Gumbel 分布。
概率密度函数(PDF)
Gumbel 分布的 PDF 如下:
公式中, μ μ 是位置系数(Gumbel 分布的众数是 μ μ ), β β 是尺度系数(Gumbel 分布的方差是 π26β2 π 2 6 β 2 )。
图1. Gumble PDF 示例图【src】
def gumbel_pdf(x, mu=0, beta=1):
z = (x - mu) / beta
return np.exp(-z - np.exp(-z)) / beta
print(gumbel_pdf(0.5, 0.5, 2))累计密度函数(CDF)
相应的,gumbel 分布的 CDF 的公式如下:
def gumbel_cdf(x, mu=0, beta=1):
z = (x - mu) / beta
return np.exp(-np.exp(-z))
print(gumbel_cdf(5, 0.5, 2))CDF 的反函数
根据 CDF 容易得到其反函数:
我们可以利用反函数法和生成服从 Gumbel 分布的随机数。
def inv_gumbel_cdf(y, mu=0, beta=1, eps=1e-20):
return mu - beta * np.log(-np.log(y + eps))
print(inv_gumbel_cdf(gumbel_cdf(5, 0.5, 2), 0.5, 2))
def sample_gumbel(shape):
p = np.random.random(shape)
return inv_gumbel_cdf(p)
print(sample_gumbel([2,3]))2. Gumbel-Max
Gumbel 随机数可以用来对多项分布进行采样。
2.1 基于 softmax 的采样
首先来看常规的采样方法。
对于 logits=(x1,…,xK) l o g i t s = ( x 1 , … , x K ) ,首先利用 softmax 运算得到规一化的概率分布(多项分布)。
然后,利用轮盘赌的方式采样。下面的代码,直接使用 numpy 的 choice 函数实现。
def softmax(logits):
max_value = np.max(logits)
exp = np.exp(logits - max_value)
exp_sum = np.sum(exp)
dist = exp / exp_sum
return dist
def sample_with_softmax(logits, size):
pros = softmax(logits)
return np.random.choice(len(logits), size, p=pros)2.2 基于 gumbel 的采样(gumbel-max)
对于某组 logits,生成相同数量的 gumbel 随机数,并加到 logits 上。 然后选择数值最大的元素的编号作为采样值。
示例代码如下:
def sample_with_gumbel_noise(logits, size):
noise = sample_gumbel((size, len(logits)))
return np.argmax(logits + noise, axis=1)可以证明,gumbel-max 方法的采样效果等效于基于 softmax 的方式。下面的实验直观地展示两种方法的采样效果。
np.random.seed(1111)
logits = (np.random.random(10) - 0.5) * 2 # (-1, 1)
pop = 100000
softmax_samples = sample_with_softmax(logits, pop)
gumbel_samples = sample_with_gumbel_noise(logits, pop)
plt.subplot(1, 2, 1)
plt.hist(softmax_samples)
plt.subplot(1, 2, 2)
plt.hist(gumbel_samples)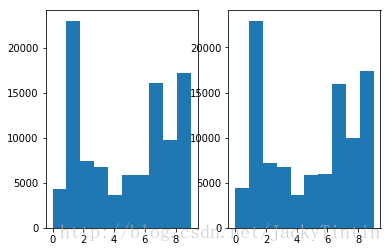
图2. Softmax 与 Gumbel-Max 采样结果对比
由于 Gumbel 随机数可以预先计算好,采样过程也不需要计算 softmax,因此,某些情况下,gumbel-max 方法相比于 softmax,在采样速度上会有优势。
3. Gumbel-Softmax
如果仅仅是提供一种常规 softmax 采样的替代方案, gumbel 分布似乎应用价值并不大。幸运的是,我们可以利用 gumbel 实现多项分布采样的 reparameterization(再参数化)。
在介绍 VAE 的时候讨论过,为了实现端到端的训练,VAE 采用的一个再参数化的技巧对高斯分布进行采样:
def guassian_sample(shape):
epsilon = K.random_normal(shape, mean=0.,std=1) # 标准高斯分布
z = z_mean + exp(z_log_var / 2) * epsilon在介绍的 VAE 里,假设隐变量(latent variables)服从标准正态分布。下面将会看到,利用 gumbel-softmax 技巧,我们可以将隐变量建模为服从离散的多项分布。
在上面的示例中,sample_with_softmax 使用了 choise 操作,而这个操作是不可导的。同样,观察 sample_with_gumbel_noise, armmax 操作同样不可导。然而,argmax 有一个 soft 版本,即 softmax。
我们首先扩展上面定义的 softmax 函数,添加一个 temperature 参数。
def generalized_softmax(logits, temperature=1):
logits = logits / temperature
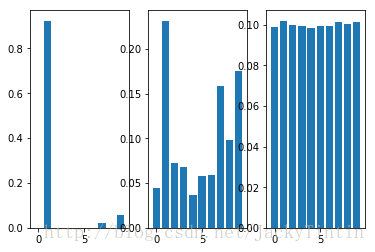
return softmax(logits)temperature 是在大于零的参数,它控制着 softmax 的 soft 程度。温度越高,生成的分布越平滑;温度越低,生成的分布越接近离散的 one-hot 分布。下面示例对比了不同温度下,softmax 的结果。
np.random.seed(1111)
n = 10
logits = (np.random.random(n) - 0.5) * 2 # (-1, 1)
x = range(n)
plt.subplot(1, 3, 1)
t = .1
plt.bar(x, generalized_softmax(logits, t))
plt.subplot(1, 3, 2)
t = 5
plt.bar(x, generalized_softmax(logits, t))
plt.subplot(1, 3, 3)
t = 50
plt.bar(x, generalized_softmax(logits, t))
将 gumbel-max 中的 argmax 操作,替换为 softmax,便实现了对于原来不可导的采样操作的软化版的近似。训练中,可以通过逐渐降低温度,以逐步逼近真实的离散分布。利用 gumbel-softmax,VAE 的隐变量可以用多项分布进行建模,一个示例见 repo。这里,仅展示一个 toy 示例(代码来自)。
import tensorflow as tf
sess = tf.Session()
def differentiable_sample(logits, temperature=1):
noise = tf.random_uniform(tf.shape(logits), seed=11)
logits_with_noise = logits - tf.log(-tf.log(noise))
return tf.nn.softmax(logits_with_noise / temperature)
mean = tf.Variable(2.)
idxs = tf.Variable([0., 1., 2., 3., 4.])
# An unnormalised approximately-normal distribution
logits = tf.exp(-(idxs - mean) ** 2)
sess.run(tf.global_variables_initializer())
def print_logit_vals():
logit_vals = sess.run(logits)
print(" ".join(["{:.2f}"] * len(logit_vals)).format(*logit_vals))
print("Logits: ")
print_logit_vals()
sample = differentiable_sample(logits)
sample_weights = tf.Variable([1., 2., 3., 4., 5.], trainable=False)
result = tf.reduce_sum(sample * sample_weights)
sess.run(tf.global_variables_initializer())
train_op = tf.train.GradientDescentOptimizer(learning_rate=1).minimize(-result)
print("Distribution mean: {:.2f}".format(sess.run(mean)))
for i in range(5):
sess.run(train_op)
print("Distribution mean: {:.2f}".format(sess.run(mean)))Logits:
0.02 0.37 1.00 0.37 0.02
Distribution mean: 2.00
Distribution mean: 2.13
Distribution mean: 2.23
Distribution mean: 2.60
Distribution mean: 2.75
Distribution mean: 3.23
可以看到,利用 gumbel-softmax 训练参数向着预期的方向改变。
import tensorflow as tf
sess = tf.Session()
mean = tf.Variable(2.)
idxs = tf.Variable([0., 1., 2., 3., 4.])
# An unnormalised approximately-normal distribution
logits = tf.exp(-(idxs - mean) ** 2)
sess.run(tf.global_variables_initializer())
def print_logit_vals():
logit_vals = sess.run(logits)
print(" ".join(["{:.2f}"] * len(logit_vals)).format(*logit_vals))
print("Logits: ")
print_logit_vals()
sample = tf.nn.softmax(logits)
sample_weights = tf.Variable([1., 2., 3., 4., 5.], trainable=False)
result = tf.reduce_sum(sample * sample_weights)
sess.run(tf.global_variables_initializer())
train_op = tf.train.GradientDescentOptimizer(learning_rate=1).minimize(-result)
print("Distribution mean: {:.2f}".format(sess.run(mean)))
for i in range(5):
sess.run(train_op)
print("Distribution mean: {:.2f}".format(sess.run(mean)))Logits:
0.02 0.37 1.00 0.37 0.02
Distribution mean: 2.00
Distribution mean: 2.32
Distribution mean: 2.65
Distribution mean: 2.87
Distribution mean: 3.10
Distribution mean: 3.36
讨论
乍看起来,gumbel-softmax 的用处令人费解。比如上面的代码示例,直接使用 softmax,也可以达到类似的参数训练效果。但两者有着根本的区别。
原理上,常规的 softmax 直接建模了一个概率分布(多项分布),基于交叉熵的训练准则使分布尽可能靠近目标分布;而 gumbel-softmax 则是对多项分布采样的一个近似。使用上,常规的有监督学习任务(分类器训练)中,直接学习输出的概率分布是自然的选择;而对于涉及采样的学习任务(VAE 隐变量采样、强化学习中对actions 集合进行采样以确定下一步的操作),gumbel-softmax 提供了一种再参数化的方法,使得模型可以以端到端的方式进行训练。
完整的 jupyter notebook 版本参见 github。
References
- http://amid.fish/humble-gumbel
- proof of Gumbel based sampling
- https://blog.evjang.com/2016/11/tutorial-categorical-variational.html
- Jang et al. CATEGORICAL REPARAMETERIZATION WITH GUMBEL-SOFTMAX.