机器学习_支持向量机SVM
文章目录
- 线性可分SVM
-
- 推导目标函数
- 计算举例
- 线性支持SVM
-
- 求解目标函数
- 非线性支持SVM
-
- 核函数 kernel function
- SMO算法(SVM系数求解)
线性可分SVM
存在一个线可以把数据分类，数据就是线性可分的。
SVM是有分割超平面两边的一些样本作为支撑点做出的支撑向量。
分割超平面
设C，D为不相交的凸集，则存在超平面P,将C，D分离。
如何选择最优超平面？（间隔最大化）
(w12+w22+…+wn2)0.5 = ||w|| (w的二范式)
直到任意点和直线，可以求出点到直线的距离：
d(xi,l) = (wx + b) / ||w|| (注：w,x为向量）
因此我们可以计算出所有点到所有可以把数据分类的超平面（二维体现为直线）的距离，选择距离直线最近距离最远的直线（超平面）就是最优超平面。
wb* = arg max(min((w*x + b) / ||w||)
得到分离超平面为:（y=0,就是分割超平面）
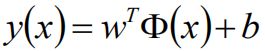
其中x的函数为某个确定的特征空间转换函数，作用是将x映射到（更高的）维度（将x1,x2,x3映射为1,x1,x2,x3,x12,x22,x32,x1x2,x1x3,x2x3; 可以由使用模型的人确认使用二阶还是三阶等)
（分离超平面问题可以等价为求解相应的（因为是凹函数）凸二次规划问题）
推导目标函数
原目标函数：
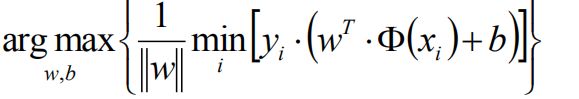
可以通过等比缩放wT的方法使|y|>=1，wT选择使过度带距离为1（min的部分为1），则目标函数为为：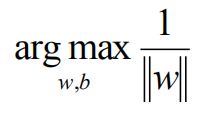
max(1/||w||) 相当于 min(||w||)
相当于 min(1/2 * ||w||2)
n为样本个数
带约束条件的极值问题----->拉格朗日乘子法得到如下方程式：（αi>=0)
原问题是极小极大min(1/2||w||2 = maxL(w,b,α))问题，它的对偶问题为极大极小问题（凸优化，min max对调）：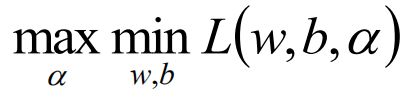
分别对w和b求偏导并令等于0：
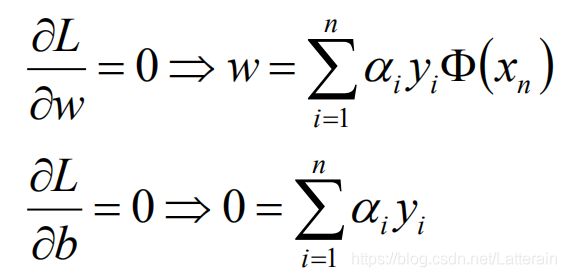
当拉格朗日乘子αi > 0时，对应样本为支撑样本，等于0则没有支撑（影响被乘0消掉）。
将得到的两个结果反代回L(w,b,α)，可以得到：
min L(w,b,α)最优解为 =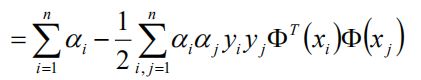 
再求对min L(w,b,α)对α的极大（添加负号可改为求极小值）：
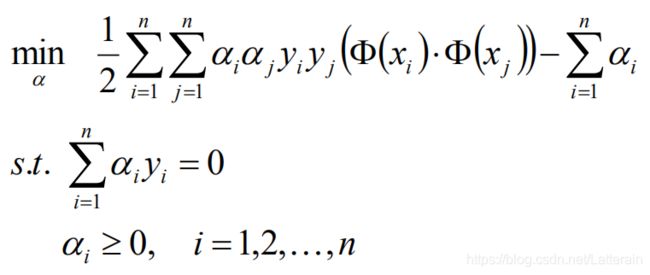
带入拉格朗日乘子α的最优解得到最优w*，b*，得到分离超平面和分类决策函数：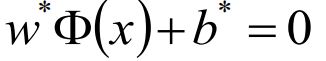
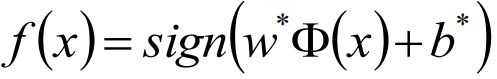
计算举例
给定三个数据点：正例点 x1=(3,3)T, x2=(4,3)T，负例点x3=(1,1)T，求线性可分支持向量机。
样本：
- （3，3，1）
- （4，3，1）
- （1，1，-1）
目标函数：
这里当α都为1时：y = 1, x1x1(向量乘积）=9+9=18
α1α2的系数为x1x2+x2*x1 = (12+9)*2 = 42
将α1+α2 = α3带入目标函数可以得到：
分别对α1，α2求偏导并令=0，则得到极值点（1.5，-1），α2 = -1，因为该点不满足α2>=0，所以最小值在边界达到。
当α1 = 0时，s = -2/13 = -0.1538
当α2 = 0时，s = -1/4=-0.25
-0.25更小，所以α2 = 0，得到α1 = 1/4，α3 = 1/4
因此，α1，α3对应的x1,x3为支持向量。
带入公式：
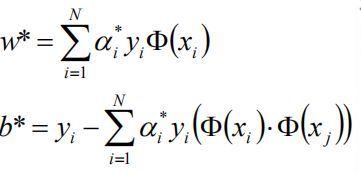
得到w1 = w2 = 0.5, b=-2
分离超平面为： 1/2x1+1/2x2-2=0
分离决策函数为：f(x) = sign(1/2x1+1/2x2-2)
线性支持SVM
软间隔最大化(soft margin maximization)
对线性不可分数据给出（略有错误）的分割面
线性可分的数据需要使用软间隔目标函数吗？
软间隔支持向量机
过渡带越宽，泛化能力越强，若线性不可分，可以增加松弛因子，松弛因子希望不要太大，所以：
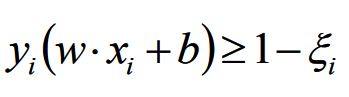
目标函数：
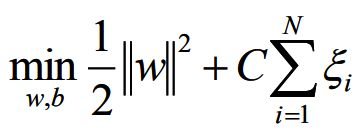
当C趋近于无穷大时，这里又会退化为线性可分SVM。C比较小，对错误的容忍程度比较高，过渡带比较宽，会有泛化能力。
如果看作loss = 目标函数，那么loss相当于L2正则+hinge损失。
求解目标函数
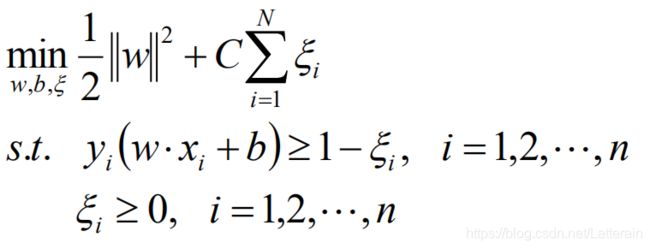
使用拉格朗日乘子法：
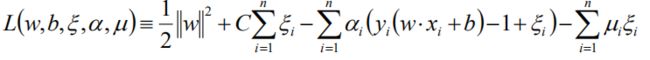
对w,b,松弛因子求偏导：
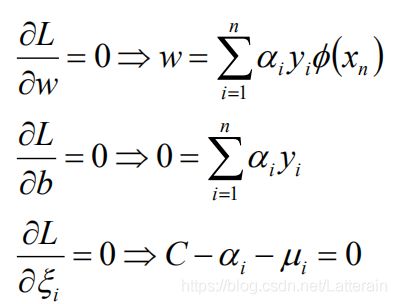
将上述式子代回拉格朗日函数中得到：
对极小求极大，为：
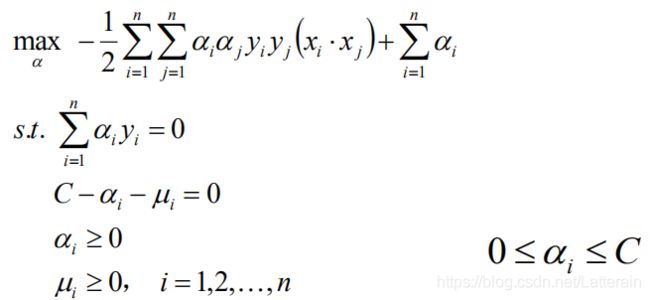
得到构造出来的最优化问题，求解得到最优解α*：
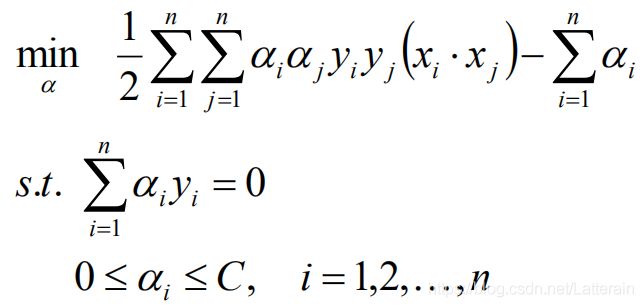
计算w*,b*（这里最优解b需要满足0<αj
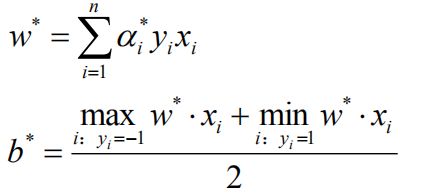
wx+b = 0
f(x)=sign(wx+b)
hinge损失的目标函数：max(1-x,0)
非线性支持SVM
核函数 kernel function
使用核解决线性不可分，依赖先验领域知识，交叉验证等选择有效核函数。（如果没有，选择高斯核函数可以减少计算量）。
线性核（C不断增大，间隔面减小）
多项式核函数:
k(x1,x2)=(x1Tx2+c)d
高斯核（如果γ值比较小，接近于直线，γ越大，分割界面非线性越强烈；C越大分割界面越小；γ = 1/(2σ2):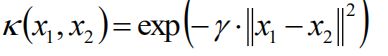
以xi为中心做指数级的衰减，求xi和 xj 的样本的相似度。任意一个样本都有一个以它为中心的高斯分布。高维空间运用SVM，低维空间加了核函数。
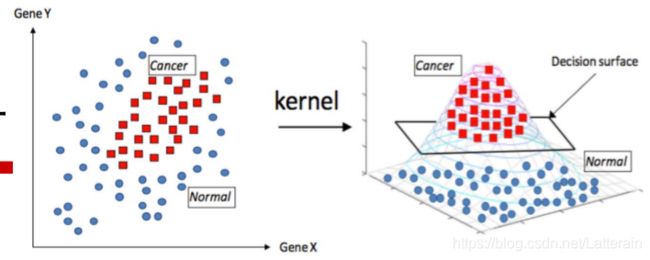
高斯核将x维映射为无穷维。
sigmoid核函数：
SMO算法(SVM系数求解)
序列化的最小优化 sequential minimal optimization
有多个拉格朗日乘子，每次只选择其中两个乘子做优化，其他因子认为是常数。（N个解的问题转换为两个变量的求解问题并且目标函数为凸的）。
SVM直接输出类别不给出后验概率，logistic回归会给出后验概率。可以SVM框架引入logistic函数输出条件后验概率。