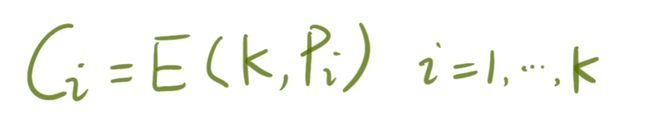分组密码模式
分组密码是一种加密方法,它应用确定性算法和对称密钥来加密文本块。
分组密码的一些不同操作模式包括 ECB(电子密码本)、CBC(密码分组链)、CFB(密码反馈)、OFB(输出反馈模式)、CTR(计数器)。
0x01 明文填充
分数密码是用来将一段明文 P 加密成密文 C(明文 P 和密文 C 的长度都可以是任意的)。
ECB 和 CBC 模式中的 AES 和3DES 等块密码算法要求其输入是块大小的精确倍数。如果要加密的明文不是精确倍数,则需要在加密前通过添加填充字符串进行填充。解密时,接收方需要知道如何以明确的方式去除填充。
很多时候,需要加密的明文并不正好是分组密码模式所要求的分组大小的整数倍,虽然明文是可以填充的,但是必须要保证填充是可逆的。
在密码学中,填充是许多不同实践中的任何一种,它们都包括在加密之前将数据添加到消息的开头、中间或结尾。在经典密码学中,填充可能包括在消息中添加无意义的短语,以掩盖许多消息以可预测的方式结束的事实。
这里看到一个很好的总结
图片来源:分组密码模式的填充_梦之痕bhl的博客-CSDN博客_分组加密算法填充模式
填充的缺点
填充的文本容易受到填充预言攻击在密码学中,填充预言攻击是一种使用加密消息的填充验证来解密密文的攻击。
在密码学中,可变长度的明文消息通常必须被填充以与底层密码兼容。该攻击依赖于一个“填充预言机”,它可以自由地响应有关消息是否正确填充的查询。填充预言攻击主要与分组密码中使用的 CBC 模式解密有关。
OAEP等非对称算法的填充模式也可能容易受到填充预言机攻击。
填充方法
在《密码工程》这本书中给出了两种最简单的填充方法,简要概括一下就是:
- P:明文
- l(P):P的长度(单位:字节)
- b:分组密码的分组大小(单位:字节)
- 在明文接下来的第一个字节中填充128,然后填充0直到整个字节长度是 b 的倍数。
(0介于1与b-1之间)
- 首先计算需要填充的字节数n(1≤n≤b)且n+l(p)是b的倍数,之后在明文后添加n个字节,每位为n
0x02 ECB
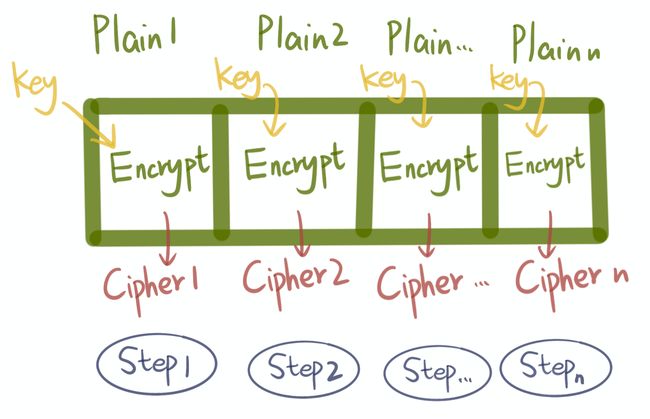
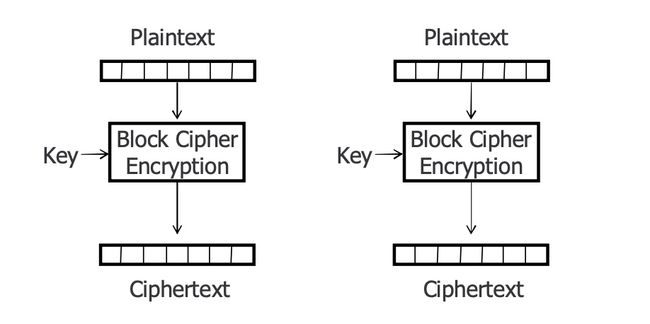
ECB(电子密码本)是最简单的加密长明文的工作模式。
ECB非常不推荐使用,原因是什么呢?
因为当两个完全相同的明文分组进行 ECB 加密工作模式后,得到的两个密文分组也是相同的。
自己画图有些抽象,找到了一个明确的图
图片来源:https://personal.utdallas.edu/~muratk/courses/crypto09s_files/modes.pdf
0x03 CBC
CBC(密码分组链)则是应用最广泛的分组密码的工作模式之一,通过将每个明文分组与前面一个密文分组进行异或,可以避免ECB模式下出现的问题。
这里就会有一个问题,C0的问题,毕竟每个明文分组是与前面一个密文分组进行异或。
图片来源:https://personal.utdallas.edu/~muratk/courses/crypto09s_files/modes.pdf
C0被称为初始化向量(initialization vector 简称IV),在《密码工程》这本书中给出了三种初始化向量的表达方式:
- 固定IV
使用相同的IV会比较不安全,因为相同的IV会使第一个分组相同,不同的待加密消息首个明文分组相同,他们的密文分组也会相同,也就造成了与ECB(电子密码本)相似的问题。 - 计数器IV
第一个消息的IV设置为0,第二个消息的IV设置为1,以此类推。也会存在一些安全问题,实际应用中很多消息内容的开头是相似的。 - 随机IV
随机IV也会存在一些问题,例如明文消息的不随机性,在CBC模式中,密文分组被用于“随机化”明文分组。
另一个问题是随机IV的IV需要让解密放知道,书中给出了一个解决方法,将随机IV作为第一个密文块放在消息所对应的密文块之前发送给接收者。
P1-Pk被加密为C0-Ck,可以发现,密文是从C0开始,比P多一个分组,不过消息的长度会增长。
4. 瞬时IV
为每一个用该密钥加密的消息分配一个唯一的值,称为瞬时值(number used once 简称 nonce)瞬时值具有唯一性,对于相同的一个密钥,瞬时值不能使用两次。
1)为消息分配一个编号,通常由从0开始的计数器提供
2)由消息编号构造唯一瞬时值,瞬时值一般对整个系统都是唯一的
3)用分组密码加密瞬时值得到IV
4)在CBC模式使用IV对消息加密
5)在密文中添加足够的消息使接收者可以恢复瞬时值
0x04 CFB
CFB(密文反馈)可将分组密码当做流密码使用,在CFB模式中,将明文拆解成s位(一般是8位,即1字节)长的分组。
明文一方面参与到对称加密的过程当中以增加复杂度,另一方面运用到异或运算中,完全过滤掉对称加密部分进行解密。
图片来源:https://personal.utdallas.edu/~muratk/courses/crypto09s_files/modes.pdf
0x05 OFB
OFB(输出反馈模式) 并不是将消息作为加密函数的输入,OFB会使用分组密码生成一个伪随机字节流(密钥流),然后使用密钥流与明文进行异或得到密文。
流密码:
使用IV值K0重复进行加密生成密钥刘K1,Kk,然后明文与密钥流进行异或得到密文。OFB的解密运算和加密运算完全相同。
图片来源:https://personal.utdallas.edu/~muratk/courses/crypto09s_files/modes.pdf
OFB的两个安全问题:
- 如果两个不同的消息使用了相同的IV,两个消息就会被相同的密钥流加密。
- 如果一个密钥分组重复出现,随后的密钥分组序列就与之前的重复。
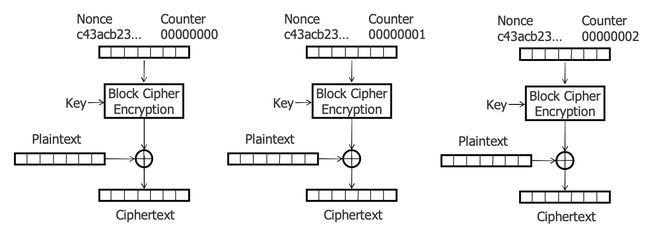
0x06 CTR
CTR(计数器模式)也是一种流密码模式,加密必须使用某种形式的唯一瞬时值。将瞬时值与计数器值联系起来并进行加密产生密钥流的一个密钥分组。
CTR加密的所有明文值都是不同的,因此所有的密文值也是不同的。同时CTR也不存在碰撞问题,CTR模式下的任意两个分组都是不相同的。
参考文章
https://en.wikipedia.org/wiki/Padding_oracle_attack
分组加密的四种模式_fw0124的博客-CSDN博客_分组加密
https://personal.utdallas.edu/~muratk/courses/crypto09s_files/modes.pdf