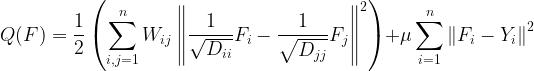读《Learning with Local and Global Consistency》

摘要

我们考虑从标记和未标记数据中学习的一般问题，这通常被称位半监督学习或转导推理。半监督学习的一种原则方法是设计一个分类函数，该函数对于已知的标记点和未标记点所揭示的内在结构具有足够的平滑性。我们提出了一个简单的算法来获得这样一个平滑的解。我们的方法在一些分类问题上产生了令人鼓舞的实验结果，并证明了对未标记数据的有效使用。

1 介绍

我们考虑常规的从标记和未标记数据中学习的问题。给定一组点集和一组标签集，前个点有标签，剩下的点没有标签。目标是预测未标记点的标签。算法的性能仅由这些未标记的点的错误率来衡量。

这样的学习问题通常被称为半监督或者转导的。由于标记通常需要昂贵的人力，而未标记的数据更容易获得，半监督学习在许多现实世界的问题中非常有用，最近吸引了大量的研究。一个典型的应用就是网页分类，手动分类的网页通常只占整个网页的很小的一部分，而未标记的例子数量很大。

半监督学习问题的关键是先验的一致性假设，即：（1）像零点可能会具有相同的标签；（2）相同结构上的点（通常称为聚类或流形）可能具有相同的标签。通常称为聚类假设。注意，第一个假设是局部的，而第二个假设是全局的。传统的监督学习算法，如k邻近，一般只依赖于第一个局部一致性假设。

为了说明半监督学习中的一致性的先验假设，让我们考虑一个根据图1(a)中的两个交织的月亮模式生成的玩具数据集。每个点都应该与其附近的点相似，而且，一个月了上的点应该比另一个月亮上的点更相似。基于RBF核的支持向量机和k-NN的分类结果分别如图1(b)和图1(c)所示。然而，根据一致性假设，这两个月亮应该按照图1(d)所示进行分类。

谱方法、随机游走、图最小切割和转导支持向量机等各种半监督学习算法的主要区别在于它们实现一致性假设的方式。将假设形式化的一个原则是设计一个分类函数，该函数对于已知的标记点和未标记点所揭示的内在结构足够光滑。这里我们提出了一个简单的迭代算法来构建这样一个光滑函数，其灵感来源于传播激活网络和扩散核，以及最近半监督学习和聚类的工作，更具体地说，来自Zhu等人的工作。该方法的基本思想是让每个点迭代地将其标签信息传递给相邻点，直到全局达到稳定状态。

本文的组织如下：第2节详细介绍了算法，并讨论了可能的变换；第3节介绍了该方法的正则化框架；第4节给出了玩具数据、数字识别和文本分类的实验结果；第5节对本文进行了总结并指出了下一步的研究方向。

2 算法

给定一组点集和一组标签集，前个点被标记为，剩余的点是未标记的。目标就是预测出未标记节点的标签。

令表示的矩阵的集合。矩阵通过将每个点标记为，来对应数据集上的分类。我们可以把理解成一个向量函数，它给每个点赋一个向量。定义一个矩阵，其中当被标记为，否则。显然，根据决策规则，与初始标签是一致的。算法如下：

1. 形成亲和矩阵，定义当时，且。
2. 构造矩阵，其中D是一个对角矩阵，对角元素等于W的第i行之和。
3. 迭代直至收敛，其中α是一个(0,1)上的参数。
4. 令表示序列的极限。将每个点标记为。

该算法可以从实验心理学（experimental psychology？）的激活网络扩散的角度直观地理解。我们首先在数据集上定义一个对角元素为零的成对关系。我们可以认为图定义在上，其中顶点集就是，边的权重就是。在第二步中，将中的权重矩阵对称归一化，这是后续迭代收敛所必需的。前两步与谱聚类完全相同。在第三步的每次迭代中，每个点从它的邻居（第一项）接收信息。值得一提的是，由于在第一步中将亲和矩阵的对角元素设为零，因此避免了自强化（self-reinforcement）。而且，由于是对称矩阵，所以信息是对称传播的。最后，将每个未标记点的标签设置为在迭代过程中接受到最多信息的类。

让我们证明序列收敛，并且。在不损失一般性的前提下，设。通过算法中使用的迭代方程，得到

(1)

由于以及[-1,1]上的特征值（注意相似于随机矩阵），

(2)（用等比数列的求和公式进行求解）

因此

对于分类来说，上式几乎等价于

(3)

现在我们可以不用迭代直接计算。这也表明迭代结果并不依赖于迭代的初始值。另外，值得注意的是实际上是一个图核或者扩散核。

现在我们讨论这种方法的一些可能的变体。最简单的修改就是在收敛后重复迭代，即，其中是任意正实数。此外，由于S与P相似，我们可以考虑在第三步中将替换为，则对应的闭式解为。用的转置替换也很有趣。分类函数就变成了。不能得到上式等价于。在实验中，我们将这些变体与原始算法进行比较。

3 正则化框架

在此，我们开发了上述迭代算法的正则化框架。与相关的代价函数定义为

(4)

其中是正则化参数。则分类函数为

(5)

代价函数右边的第一项是平滑约束，这意味着一个好的分类函数在相邻点之间不应该有太大的变化。第二项是拟合约束，这意味着一个好的分类函数不应该对初始标签赋值有太大的改变。这两个竞争约束之间的权衡被一个正的参数捕获。注意，拟合约束既包含有标签的数据，也包含无标签的数据。

我们可以将平滑项理解为局部变化量的和，即函数在相邻点之间的局部变化量。正如我们所提到的，涉及成对关系的点可以被认为是一个无向加权图，其权重表示成对关系。然后在每条边测量局部变化。我们不是简单地通过边两端函数值的差来定义边上的局部变化。平滑项本质上是计算局部变化之前将函数值在每个点上的边之间分割，分配给每条边的值与它的权值成比例。

求关于的微分，我们得到

上式可以转换为

引入两个新的变量

注意到。得到

因为是可逆的，我们得到

(6)

这个式子是上述迭代算法的封闭解。

类似地，我们可以为变体和开发优化框架。由于篇幅有限，我们省略了讨论。

4 实验

我们使用k-NN和one-vs-rest支持向量机作为基线，然后把我们的方法和它的两个变体进行比较：(1)；和(2)。我们还与Zhu等人的调和高斯场方法与类质量归一化（CMN）相比较，后者与我们的方法密切相关。据我们所知，如果只有很少的标记点可用，就没有可靠的模型选择方法。因此，我们让所有算法使用各自的最优参数，除了在我们方法种使用的参数及其变体简单地固定在0.99。

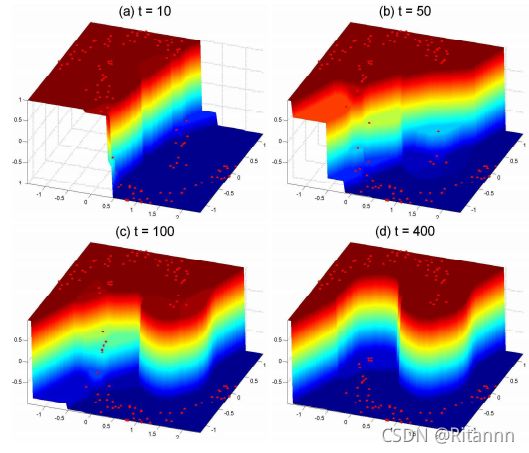
图2：两个月亮的模式分类。从(a)到(d)，我们的迭代算法在t从1增加到400的收敛过程。注意，初始标签信息是沿着月亮扩散的。

 

图3：随着月亮的增加，实值分类函数相对于两个月亮模式变得越来越平。注意(d)种出现了两个清晰的月亮。

 

图4：具有全局一致性的监督分类器给出的平滑分类结果：(a)具有RBF核的支持向量机给出的分类结果；(b)使用一致性方法平滑支持向量机的结果。

4.1 玩具问题

在本实验中，我们考虑了第1节种提到的玩具问题（图1）。亲和矩阵由PBF核定义，但对角元素被设为零。我们迭代算法的收敛过程如图2(a)-2(d)所示，t从1增加到400。注意，初始标签信息是沿着月亮扩散的。一致性假设本质上是指一个好的分类函数应该在由大量数据聚合而成的相干结构上缓慢变化。这个玩具问题可以很清楚地说明这一点。我们顶一个函数，因此决策函数为符号，这相当于第2节种描述的决策规则。在图3中，我们显示相对于图3(a)-3(d)中的两个月亮模式，随着t的增加，变得依次平坦。注意，在图3(d)中出现了两个清晰的月亮。

我们方法的基本思想是构造一个光滑函数。很自然地考虑使用这种方法来改进监督分类器，平滑其分类结果。换句话说，我们使用有监督分类器给出的分类结果作为算法的输入。图4中的一个玩具问题演示了这个猜想。图4(a)为基于RBF核的SVM分类结果。然后在我们的方法中将这个结果赋给。我们方法的输出如图4(d)所示。注意，被支持向量机分类错误的点被一致性方法平滑成功。

4.2 数字识别

在本实验中，我们使用USPS手写16x16位数据集进行分类。我们在实验中使用数字1、2、3、4作为四个类。每个类有1269、929、824和852个示例，总共有3874个。

k-NN中的k设为1。支持向量机的RBF核的宽度设置为5，调和高斯场方法的RBF核的宽度设置为1.25。在我们的方法及其变体中，亲和矩阵由与调和高斯方法相同宽度的RBF核构造，但对角线元素设为0。图5的左面板总结了超过100次试验的平均测试误差。选择样本，以便每个类至少包含一个标记点。我们的一致性方法及其变体明显优于传统的监督学习算法k-NN和SVM，也优于调和高斯方法。

注意，我们的方法不要求亲和矩阵是正定的。这使我们能够以一种优雅的方式合并关于数字图像不变性的先验知识，例如，使用抖动核（jittered kernel）来计算亲和矩阵。已知其他核方法在此方法中存在问题。在我们的例子中，对于30个标记点，抖动1像素的平移会导致大约0.01的错误率。

图5：左面板：USPS手写16x16数字数据集的数字识别率（包含从1到4的数字子集）。右面板：在8014维空间中，3970个文档向量的文本分类错误率。选择样本，以便每个类至少包含一个标记点。

4.3 文本分类

在本实验中，我们研究了使用20-newsgroups组数据集的文本分类任务。我们从版本20-news-18828中选择了包含汽车、摩托车、棒球和曲棍球的休闲主题。文章使用Rainbow软件包处理的，有以下选项：(1)在技术之前通过Porter stemmer传递所有单词；(2)抛出SMART系统停止列表上的任何令牌；(3)跳过任何标题；(4)忽略出现在5个或更少文档中的单词。没有进行进一步的预处理。在8014维空间中去除空文档，得到3970个文档向量。最后将文档规范化为TFIDF表示。

定义点和之间的距离为。k-NN中的k设为1。支持向量机的RBF核的宽度设置为1.5。调和高斯方法的RBF核的宽度设置为0.15。在我们的方法中，亲和矩阵由与调和高斯方法相同宽度的RBF核构造，但对角元素设为0。在图5的右面板中总结了超过100次试验的平均测试误差。选择样本，以便每个类至少包含一个标记点。

有趣的是，当标记点的数量为4时，即每个类有一个标记点时，调和法非常好。我们认为这是因为数据集中不同类的比例几乎相等，所以有四个标记点时，比例恰好被估计准确。然而，如果使用稍微多一点的标记点，例如10个标记点，调和方法就会变得很糟，这导致了相当糟糕的估计。随着标记点的数量进一步增加，调和方法再次很好地工作，并比我们的方法好，因此类的比例再次估计成功。然而，我们的决策规则要简单得多，它实际上对应于所谓的朴素阈值，即调和方法的基线。

5 总结

半监督学习问题的关键是一致性假设，这本质上要求分类函数对于大量标记点和未标记点所揭示的内在结构足够平滑。我们提出了一种简单的算法来获得这样的解决方案，在玩具数据、数字识别和文本分类等试验中证明了对未标记数据的有效利用。在进一步的研究中，我们将着重于模型的选择和理论分析。