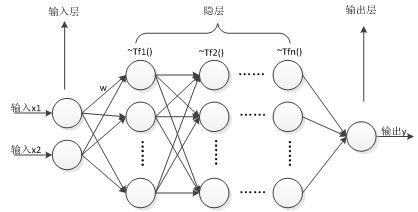
一起看看matlab工具箱内部是如何实现BP神经网络的
目录
一、源码复现效果
二、训练主流程
三、效果差异来源分析
四、不同训练方法的效果对比
五、相关文章
原创文章,转载请说明来自《老饼讲解-BP神经网络》bp.bbbdata.com
如果我们直接使用梯度下降法去求解BP神经网络,
往往没有matlab工具箱的效果那么好。
这个问题曾经困扰笔者好一段时间,
那我们不妨扒出源码看看,matlab工具箱是怎么实现BP神经网络的,
为什么我们自写的训练效果没有工具箱BP神经网络的好。
一、源码复现效果
扒出matlab工具箱梯度下降traingd算法源码,梳理算法流程后,
自写代码求得的一个2隐层BP神经网络的权重
调用工具箱newff求得的权重:
可以看到,两个结果是一样的,说明完全理解和复现了工具箱的BP神经网络训练逻辑。
二、训练主流程
BP神经网络梯度下降法主流程如下
先初始化权重阈值,
然后用梯度迭代权重阈值,
如果达到终止条件则退出训练
终止条件为:误差已达要求、梯度过小或者达到最大次数
代码如下:
function [W,B] = traingdBPNet(X,y,hnn,goal,maxStep)
%------变量预计算与参数设置-----------
lr = 0.01; % 学习率
min_grad = 1.0e-5; % 最小梯度
%---------初始化WB-------------------
[W,B] = initWB(X,y,hnn); % 初始化W,B
%---------开始训练--------------------
for t = 1:maxStep
% 计算当前梯度
[py,layerVal] = predictBpNet(W,B,X); % 计算网络的预测值
[E2,E] = calMSE(y,py); % 计算误差
[gW,gB] = calGrad(W,layerVal,E); % 计算梯度
%-------检查是否达到退出条件----------
gradLen = calGradLen(gW,gB); % 计算梯度值
% 如果误差已达要求,或梯度过小,则退出训练
if E2 < goal || gradLen <=min_grad
break;
end
%----更新权重阈值-----
for i = 1:size(W,2)-1
W{i,i+1} = W{i,i+1} + lr * gW{i,i+1};%更新梯度
B{i+1} = B{i+1} + lr * gB{i+1};%更新阈值
end
end
end(这里的代码复现我们屏蔽掉归一化处理、泛化验证这两个算法通用操作)
三、效果差异来源分析
效果差异来源
主流程与常规算法教程并没有差异,
那么为什么matlab的结果会更好呢,
原因主要在初始化上,
很多教程,都建议随机初始化,
而实际上,matlab工具箱使用的是nguyen_Widrow法进行初始化
nguyen_Widrow法
nguyen_Widrow法初始化思想如下:
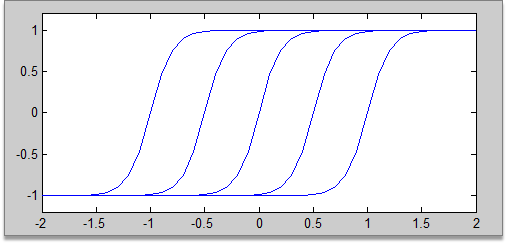
以单输入网络为例,它会把网络初始化成以下的形式:
它的目的就是让各个隐节点均匀分布在输入数据的范围。
理由就是,如果BP神经网络最后每个神经元都是被充分利用的,
那么应该较近似以上的分布(对输入范围全覆盖、每个神经元都充分利用),
与其随机初始化再慢慢调整,不如一开始就给出这样一个初始化。
该方法的原文为:
Derrick Nguyen 和Bernard Widrow的《Improving the learning Speed of 2-Layer Neural Networks by Choosing Initial Values of the Adaptive Weights 》
四、不同训练方法的效果差异
效果比较
而作者又用traingd、traingda、trainlm进行效果对比,
发现同一个问题,
traingd训练不出来的,traingda能训练出来,
而traingda训练不出来的,trainlm又能训练出来。
即在训练效果上
traingd< traingda < trainlm
那么,如果我们直接使用自写的梯度下降法算,
仍然是远远不如我们使用matlab工具箱效果好的。
matlab的BP神经网络默认用的是trainlm算法
原因简述
那traingda为什么比traingd强呢,trainlm又为什么比traingda强呢?
经过扒取源码分析,主要是traingda中加入了自适应学习率,
而trainlm则是利用了二阶导数的信息,使学习速度更加快。
五、相关文章
复现完整代码见:
《重写traingd代码(梯度下降法)》
初始化方法见:
《BP神经网络初始化》
这就是matlab神经网络工具箱中梯度下降法的算法逻辑了,如此简单~!