自学神经网络系列——7 前馈神经网络前置知识
7 前馈神经网络前置知识
- 一 感知机算法
-
- 1 模型形式
- 2 线性分类器
- 3 存在问题
- 4 python实现
-
- (1)与门
- (2)与非门
- (3)或门
- 5 多层感知机解决异或问题
- 二 神经网络结构
-
- 1 常见的激活函数
-
- (1)sigmoid 激活函数
- (2)Tanh激活函数
- (3)Relu激活函数
- (4)Leaky Relu
- (5)Softplus激活函数
- (6)其他激活函数
- 2 网络结构
-
- (1)前馈神经网络
- (2)循环神经网络
- (3)图神经网络
一 感知机算法
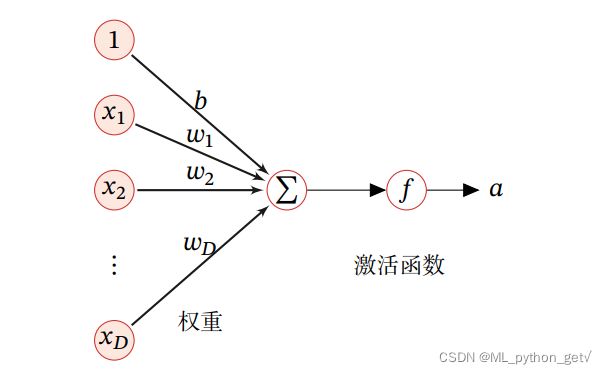
1 模型形式
z = ∑ i = 0 D w d x d + b z = \sum_{i=0}^D w_dx_d+b z=i=0∑Dwdxd+b
2 线性分类器
- 接受多个输入信号,输出一个信号
- 神经元:对输入的信号进行加权,如果加权数满足某一条件则输入1,否则输出0
- 权重代表了信号的重要程度
3 存在问题
-
与门:只有两个输入都为1时才输出1,其他情况输出0
-
与非门:颠倒与门输出情况,只有两个输入都为1时才输出0,否则输出1
-
或门: 只要有一个输入为1,那么输出1,只有全部输入为0,才输出0
-
异或门:只有一个输入为1时,才会输入1,如两个输入为1时,输出0,如图1所示
-
感知机算法不能处理异或门
感知机算法的思想:只要调整感知机的参数即可实现感知机在不同门之间的切换; 参数调整交给计算机来做,让计算机决定是那种门。
4 python实现
(1)与门
def AND(x1,x2):
'''与门的实现'''
w1,w2,theta = 0.5,0.5,0.7
tmp = x1*w1+x2*w2
if tmp<=theta:
return 0
elif tmp>theta:
return 1
# 测试函数
print(AND(1,1)) # 1
print(AND(0,0)) # 0
print(AND(1,0)) # 0
print(AND(0,1)) # 0
# 使用偏置 和numpy实现
def AND(x1,x2):
import numpy as np
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.7 # 阈值,调整神经元被激活的容易程度
tmp = np.sum(w*x) +b
if tmp<=0:
return 0
elif tmp>0:
return 1
# 测试 和普通实现一样
print(AND(1,1)) # 1
print(AND(0,0)) # 0
print(AND(1,0)) # 1
print(AND(0,1)) # 1
(2)与非门
- 输出正好相反,权重和偏置互为相反数即可
def NAND(x1,x2):
'''与非门'''
import numpy as np
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
tmp = np.sum(w*x)+b
if tmp <=0:
return 0
elif tmp>0:
return 1
# 测试
print(NAND(1,1)) # 0
print(NAND(1,0)) # 1
print(NAND(0,1)) # 1
print(NAND(0,0)) # 1
(3)或门
- 偏置绝对值小于0.5即可 更容易激活
def OR(x1,x2):
import numpy as np
x = np.array([x1,x2])
w = np.array([0.5,0.5]) # 只要不是两个输入都去0, 就输出1
b = -0.2
tmp = np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
OR(1,1)
OR(0,1)
OR(1,0)
OR(1,1)
5 多层感知机解决异或问题
- 异或门:用直线无法分开
- 引入非线性:叠加层的感知机
- 经过与非门得到S1 或门得到S2 可以看到二者通过与门即可到的异或门的结果
- 多层感知机:存在多个线性分类器,通过与门即可实现对非线性的拟合
def XOR(x1,x2):
s1 = NAND(x1,x2) #与非门
s2 = OR(x1,x2) # 或门
y = AND(s1,s2) # 相当于对两条进行组合
return y
# 测试
XOR(1,1)
XOR(0,0)
XOR(1,0)
XOR(0,1)
二 神经网络结构
基本思想:上一节中,多层感知机即多个线性函数的通过逻辑运算符实现非线性分类,很自然的联想到对线性函数进行非线性变换使其能够解决非线性可分的分类问题。这类非线性变换在神经网络中是激活函数。
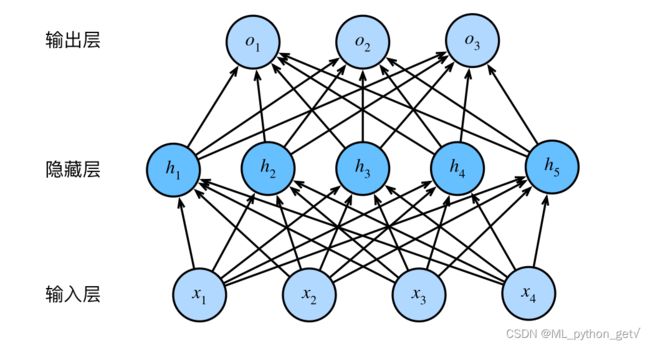
神经网络:利用带有激活函数的多层感知机模型来学习非线性特征表达的统计模型。常见的全连接神经网络结构如图2所示:
1 常见的激活函数
- 任意曲线都可以用激活函数来近似:多项式函数可以完美拟合空间中的任一点
- 任意曲线都是一些激活函数的和,类似样条估计的思想。
- 神经网络分为多层:每一层使用相同的激活函数,这些激活函数仅仅权重和偏置不同
- 两个ReLU函数才能构造一个阶跃函数(取值0,1)或者sigmoid函数
- 所以同样情况下ReLU的激活函数(神经元)需要增加一倍
(1)sigmoid 激活函数
- 机器学习中定义的sigmoid激活函数就是Logstic分布的CDF,形式如下:
σ ( x ) = 1 1 + e x p ( − x ) \sigma(x) ={1\over1+exp(-x)} σ(x)=1+exp(−x)1
-
逻辑分布属于指数分布族
Logstic分布经常用于周期型分析,例如经济的萧条、复苏、繁荣、衰退,开始经济增长缓慢,经济复苏后开始快速增长,繁荣阶段后经济开始停滞不前,增速放缓,最后甚至开始衰退,继续进入萧条阶段,较为符合logistic分布。
-
分布函数具有0-1的特性,所以其输出可以看作概率分布,用于分类。
-
分布函数中间激活取值,两边处于抑制状态的特性,符合神经元特点
-
梯度消失问题
- 两端导数接近0
- 梯度小于1,链式法则传导太长时,产生梯度消失问题
(2)Tanh激活函数
- Tanh激活函数形式
t a n h ( x ) = e x p ( x ) − e x p ( − x ) e x p ( x ) + e x p ( − x ) tanh(x) = {exp(x)-exp(-x)\over exp(x)+exp(-x)} tanh(x)=exp(x)+exp(−x)exp(x)−exp(−x)
- Tanh可以看作sigmoid激活函数的变形,两者都属于指数函数族
t a n h ( x ) = 2 σ ( 2 x ) − 1 tanh(x) = 2\sigma(2x)-1 tanh(x)=2σ(2x)−1
- tanh(x) 值域 为(-1,1)符合中心化特点,sigmoid(x)值域为(0,1) 输出恒大于0
(3)Relu激活函数
- Relu激活函数是目前神经网络中最常用的激活函数,形式如下:
R e l u ( x ) = { x , x > 0 0 , x < = 0 Relu(x)=\begin{cases} x ,& x>0 \\ 0,& x<=0 \\ \end{cases} Relu(x)={x,0,x>0x<=0
- 单侧抑制:左饱和,坐标轴无限远处,函数值不再发生明显变化的现象称为饱和,sigmoid函数和Tanh函数是两端饱和函数,Relu激活函数则是左饱和;
- 宽兴奋边界:激活区域较广,正向输入都可以被激活
- 缓解梯度消失问题:导数为1,一定程度缓解梯度消失问题
- Relu死亡问题:当输入为异常值时,Target的预测会有很大的偏差,那么在反向传播(反传的是误差),会使偏置b的更新发生偏移(偏置偏移问题),同时可能使b为负,偏置为负,这样来再多的样本也会使计算出来的隐藏层为负,经过relu激活函数时,梯度为0,参数不再更新,这种现象被称为死亡Relu问题。
(4)Leaky Relu
- 为了改善Relu函数,避免死亡Relu问题,Leaky Relu激活函数再输入x为负时,引入一个小梯度,如下:
L e a k y R e l u ( x ) = { x i f x > 0 γ i x i f x < = 0 Leaky Relu(x)=\begin {cases} x & if \space x>0 \\ \gamma_i x & if \space x<=0\\ \end{cases} LeakyRelu(x)={xγixif x>0if x<=0
- 其中 γ i \gamma_i γi可以是带估参数,也可以是一个常数
- ELU激活函数:令 γ i x = γ i ( e x p ( x ) − 1 ) \gamma_ix=\gamma_i(exp(x)-1) γix=γi(exp(x)−1)
(5)Softplus激活函数
- Relu 函数的平滑版本,形式如下:
S o f t p l u s ( x ) = l o g ( 1 + e x p ( x ) ) Softplus(x) = log(1+exp(x)) Softplus(x)=log(1+exp(x))
- 导数为sigmoid激活函数,梯度消失问题会无稀疏激活性
- 单侧抑制、宽兴奋边界
(6)其他激活函数
-
Swish函数: s w i s h ( x ) = x σ ( β x ) swish(x) = x \sigma(\beta x) swish(x)=xσ(βx)
- σ函数作为一种门控单元,控制x的输出大小
- 介于Relu与线性函数之间的非线性插值函数
-
Gelu函数: G e l u ( x ) = x P ( X < = x ) Gelu(x) = xP(X<=x) Gelu(x)=xP(X<=x)
- 使用高斯函数作为门控单元,控制x的输出
-
Maxout单元
- 分段线性函数
- 利用上一层神经元的所有输出而不是其中一个输出,获得多个参数向量
- 输出取线性变换后的多个输出的最大值
2 网络结构
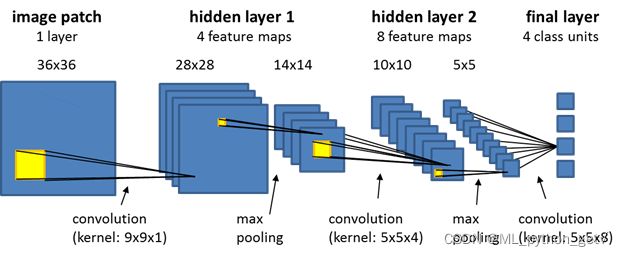
(1)前馈神经网络
- 只能朝一个方向传播,没有反向的信息传播
- 全连接神经网络
- 与全连接区别于:不同层神经元之间部分连接、共享权重(卷积核)减少参数估计个数
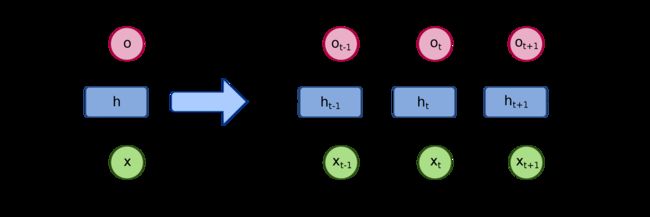
(2)循环神经网络
(3)图神经网络
参考资料:
1.邱锡鹏:《神经网络与深度学习》
2.李沐:《动手学深度学习》