深度学习：基础概念陈述及P-R曲线绘制案例(Python)

一.概念陈述

1.1引例

人类具有较强的学习能力，普通孩童经过训练后能够通过一定特征辨别出家中的自行车与小汽车

如小汽车具有四轮而形似方块，自行车仅具两轮而形体略小

一段时间后，该孩童能够对于新样本进行正确分类，例如对于邻居家的汽车/自行车能够正确区分

由此可见人类具有从一定规模数据中进行归纳的能力

1.2机器学习与深度学习

机器学习(Machine Learning):

• 对研究问题进行模型假设。
• 利用计算机从训练数据中学习得到模型参数。
• 最终对数据进行预测和分析的一门学科。
  

深度学习(Deep learning)：

• 一种实现机器学习的技术，是机器学习重要的分支。
• 源于人工神经网络的研究。深度学习的模型结构是一种含多隐层的神经网络。
• 通过组合低层特征形成更加抽象的高层特征。

1.3基础概念

概念	功能	举例
算法(Algorithm)	用于训练模型的方法	简单线性回归算法、 SVM、逻辑回归算法 KNN算法、k-means算法、
模型 (Model)	算法所训练出的结果	= 1 + 0
参数 (Parameter)	用于描述一个具体的模型的参数， 其取值可以由训练集训练得出	1和0
超参数(Hyperparameter)	控制机器学习过程并确定学习算法 最终学习的模型参数值的参数	如Splitting ratio, learning rate, # of clusters

1.4机器学习与统计学的对比

目前，数据分析的主要实现方式中包括机器学习与统计学，因此可以对二者进行一个辨析。

序号	机器学习	统计学
1	学习（Learn）	拟合（Fit）
2	算法（Algorithm）	模型（Model）
3	分类器（Classifier）	假设（Hypothesis）
4	无监督学习（Unsupervised Learning）	聚类（Clustering） 密度估计（Density Estimation）
5	有监督学习（Supervised Learning）	分类（Classification） 回归（Regression）
6	网络（Network）/图（Graph）	模型（Model）
7	权重（Weights）	参数（Parameters）
8	特征（Feature）矩阵	自变量（Independent Variable）
9	目标（Target）向量	因变量（Dependent Variable）

二.数据集(dataset)

2.1数据集的数学表示

数据集在数学上通常表示为{(x₁,y₁),(x₂,y₂),…,(x_i,y_i),…}的形式

• 其中x_i为样本特征。由于样本一般有多个特征，因而x_i = {x_i¹,x_i²,…,x_iⁿ}^T。
• 而y_i表示样本 的类别标签。

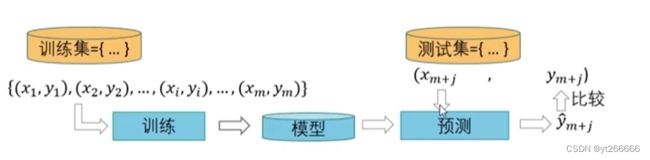
2.2训练集和测试集

在有监督学习中数据通常分为训练集和测试集两部分，有时对训练集进一步划分为训练集和验证集。

• 训练集(training set):用来训练模型，被用来学习得到系统的参数取值。
• 测试集(testing set):用于最终报告模型的评价结果，因此在训练阶段测试集中的样本是不可见的。
• 验证集(validation set):与测试集类似，也用于评估模型的性能，不过验证集主要用于模型选择和调整超参数，因而一般不用于报告最终结果。

2.3数据集拆分方法

留出法(Hold-Out Method):

1. 将数据随机分为两组，一组做为训练集，一组做为测试集。
2. 利用训练集训练分类器，然后利用测试集评估模型，记录最后的分类准确率为此分类器的性能指标。

优点:

1. 处理简单

缺点:

1. 数据集的拆分情况随机出现
2. 基于这种数据集拆分基础上的性能评价结果不够稳定

K折交叉验证

过程:

1. 数据集被分成K份（K通常取5或者10）
2. 不重复地每次取其中一份做测试集，用其他K‐1份做训练集训练， 这
   样会得到K个评价模型
3. 将K次评价的性能求均值，并作为最后评价结果。

评价:

• 相较于留出法的操作要繁琐了许多，但最终的评估结果变得十分稳定，更具有代表性。

分层抽样策略(Stratified k‐fold):

将数据集划分成k份，特点在于，划分的k份中，每一份内各个类别数据的比例和原始数据集中各个类别的比例相同。

2.4网格搜索

我们常用网格搜索来对超参数进行调整

超参数(Hyperparameter): 指在学习过程之前需要设置其值的一些变量，而不是通过训练得到的参数数据。如深度学习中的学习速率等就是超参数。

网格搜索举例:

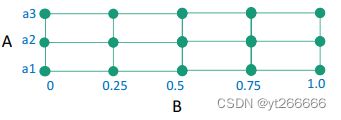
1. 假设模型中有2个超参数： A和B。 A的可能取值为{a1, a2, a3}， B的可能取值为连续的，如在区间[0,1]。
2. 由于B值为连续，通常进行离散化，如变为{0, 0.25, 0.5, 0.75, 1.0}
3. 如果使用网格搜索，就是尝试各种可能的(A, B)对值，找到能使的模型取得最高性能的(A, B)值对。
4. 此处的最高性能可以使用交叉验证的方法求得其k次评价的性能均值。

三.分类问题及性能度量

3.1分类问题

概念：

• 分类问题是有监督学习的一个核心问题。
• 分类解决的是要预测样本属于哪个或者哪些预定义的类别，此时输出变量通常取有限个离散值

阶段：

1. 从训练数据中学习得到一个分类决策函数或分类模型，称为分类器（classifier）
2. 利用学习得到的分类器对新的输入样本进行类别预测。

类别:

• 存在两类分类问题与多类分类问题。
• 多类分类问题也可以转化为两类分类问题解决。
• 比如采用一对其余(One-vs-Rest)的方法：将其中一个类标记为正类，然后将剩余的其它类都标记成负类。

3.2性能度量

假设只有两类样本，即正例(positive)和负例(negative)。 通常以关注的类为正类，其他类为负类

	预测为P	预测为N
实际为P	TP	FN
实际为N	FP	TN

分类性能度量—准确率

分类准确率(accuracy)：分类器正确分类的样本数与总样本数之比:

在此表格中 accuracy = (TP+TN)/(TP+FN+FP+TN)

分类性能度量—精确率和召回率

精确率(precision): 反映了模型判定的正例中真正正例的比重。

在此表格中 precision = TP/(TP+FP)

召回率(recall): 反映了总正例中被模型正确判定正例的比重。

在此表格中 recall = TP/(TP+FN)

分类性能度量—P-R曲线

在图像中绘制出P-R曲线，横坐标为recall，纵坐标为precision。

而该曲线与坐标轴围成的面积区域为Area(Area Under Curve)

Area避免了精确率与召回率的局限性，而是反映了全局性能。

分类性能度量——F值

F值(—)是 精确率和召回率的调和平均:

— =((1+²)×precision×recall)/(²×precision+recall)

而其中较为常用的则是F₁：

F₁— = (2×precision×recall)/(precision+recall)

分类性能度量——ROC

横轴:假正例率 fp rate = FP/N

纵轴:真正例率 tp rate = TP/P

ROC(receiver operating characteristic curve)

• 中文名为“受试者工作特征曲线”
• 描述了分类器在真正例率和假正例率间的比重
• ROC曲线下的面积为ROC-AUC
• 通常该面积越大 分类器效果更好

四.回归问题及性能度量

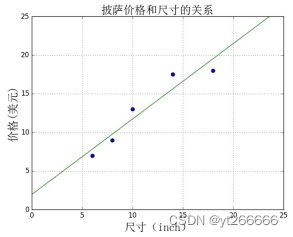
4.1回归问题

回归分析(regression analysis)

• 是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
• 回归的输出通常为实数数值。

4.2性能度量

对于回归问题的常用评价指标

• 平均绝对误差 MAE
• 均方误差 MSE
• Log loss 交叉熵损失
• R方值

平均绝对误差 MAE

是绝对误差损失的期望值

如果
$$\begin{gathered} y是第i个样本的预测值 \\ {y}_i是相应的真实值 \\ 在n_{samples}个测试样本上 \end{gathered}$$
平均绝对误差MAE的定义如下
$$MAE(y,y)=\frac{1}{n_{samples}}\sum _{i=0}^{n_{samples}-1}|y_i-y|$$
均方差 MSE

该指标对应于平方误差损失 (squared error loss) 的期望值。

如果
$$\begin{gathered} y是第i个样本的预测值 \\ {y}_i是相应的真实值 \\ 在n_{samples}个测试样本上 \end{gathered}$$
均方差MSE的定义如下
$$MSE(y,y)=\frac{1}{n_{samples}}\sum _{i=0}^{n_{samples}-1}{|y_i-y_i|}^2$$
均方根误差RMSE是均方误差MSE的平方根。

交叉熵损失 Log loss

常用于评价逻辑回归LR和深井网络

假设某样本的真实标签取值为(0或1)，概率估计为p = pr(y=1)

每个样本的log loss是对分类器给定真实标签的负log似然估计

L_log(y,p)=-log(pr(y|p))=-ylog§+(1-y)log(1-p)

五.案例:绘制Iris数据集P-R曲线

5.1鸢尾花数据

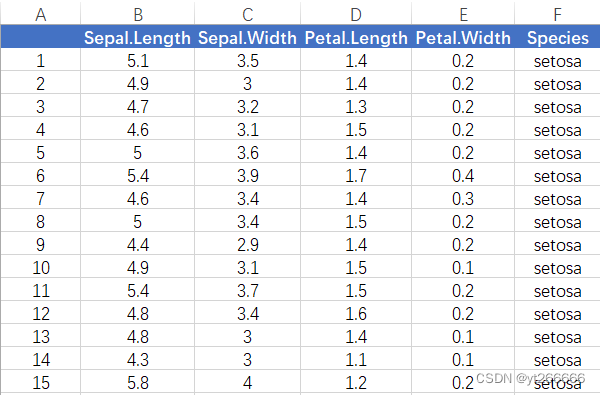
• 三类鸢尾花,分别为:Secosa,Versicolor,Virginica。
• 每个样本包含4个特征，1个类别标签。
• 共有150个样本，3类，每类50个样本。

利用EXCEL打开本地的鸢尾花数据集如下:

链接：鸢尾花数据集-百度网盘

提取码：adgf

5.2环境准备(sklearn)

方法一：安装Anaconda

直接Anaconda官网安装即可 里面集成了许多重要模块 相应的配置教程能够在CSDN博客中找到。

方法二：创建虚拟环境+pip安装

1.选择工作区 我选择了D盘下的python opencv文件夹(个人自己决定 不必保持一致)

2.cmd环境下安装virtualenv 便于创建虚拟环境 pip install virtualenv

3.在你选定的工作区下创建虚拟环境 如virtualenv venv

4.在venv/Scripts中进入cmd环境 输入activate激活虚拟环境

5.安装必须的包

在激活的虚拟环境中执行下列语句:

pip install Numpy -i https://pypi.douban.com/simple

pip install scipy -i https://pypi.douban.com/simple

pip install matplotlib -i https://pypi.douban.com/simple

pip install scikit-learn -i https://pypi.douban.com/simple

pip install jupyter -i https://pypi.douban.com/simple

能够成功导入而不报错

至此就安装好了必备的环境 将使用jupyter notebook进行代码的编写

5.3完整源码详解

"""
# 绘制P-R曲线(精确率-召回率曲线)
"""
print(__doc__)

# 绘制P-R曲线(精确率-召回率曲线)

# plt：绘图
import matplotlib.pyplot as plt
# np：处理矩阵运算
import numpy as np
# svm：支持向量机
# datasets：数据集模块 后续使用该模块导入"鸢尾花数据集"
from sklearn import svm, datasets
# precision_recall_curve：精确率-召回率曲线
from sklearn.metrics import precision_recall_curve
# average_precision_score：根据预测分数计算平均精度（AP）
from sklearn.metrics import average_precision_score
# train_test_split：训练集与测试集的拆分模块
from sklearn.model_selection import train_test_split
# label_binarize：标签的二处理
from sklearn.preprocessing import label_binarize
# OneVsRestClassifier：一对其余 每次将某一类作为正类 其余作为负类
from sklearn.multiclass import OneVsRestClassifier

# 导入鸢尾花数据集
iris = datasets.load_iris()
# x为数据集的样本特征矩阵 150*4
x = iris.data 
# y是类别标签矩阵 150*1
y = iris.target
y

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

# 将y转化为150*3的矩阵 目的是为转化为两类的分类问题 y中数值不是0即是1
# Binarize the output 标签二值化 将三个类转为001，010，100的格式,
# 因为这是个多类分类问题 转化完成后将采用OneVsRestClassifier策略转化为二类分类问题
y = label_binarize(y, classes=[0, 1, 2])

# y.shape = (150, 3)
# n_classes为y的列数 
# 即n_classes=3
n_classes = y.shape[1]
print(y)

[[1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [1 0 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 1 0]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]
 [0 0 1]]

# Add noisy features 增加了800维的噪声特征
random_state = np.random.RandomState(0)
n_samples, n_features = x.shape
# n_samples=150  n_features=4

(150, 4)

# 在150×4的矩阵后增加了150*800的矩阵
x = np.c_[x, random_state.randn(n_samples, 200*n_features)]

# 进行训练集与测试集的拆分 比例为0.5
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=.5,random_state = random_state)

# 构建分类器 进行二类问题的转化
classifier = OneVsRestClassifier(svm.SVC(kernel='linear',probability=True,random_state=random_state))
# 利用训练集进行拟合 并将测试集传入获取对测试集中y值的预测
y_score = classifier.fit(x_train,y_train).decision_function(x_test)

# 将y_score这个预测值与每个样本的真实值进行比较
precision = dict()
recall = dict()
average_precision = dict()
for i in range(n_classes):
    #下划线是返回的阈值。作为一个名称：此时“_”作为临时性的名称使用。
    #表示分配了一个特定的名称，但是并不会在后面再次用到该名称。
    precision[i], recall[i],_ = precision_recall_curve(y_test[:,i],y_score[:,i])
    average_precision[i] = average_precision_score(y_test[:,i],y_score[:,i])
    # 切片 第i个类的分类结果性能

# Compute micro-average curve and area. ravel()将多维数组降为一维
precision['micro'],recall['micro'],_ = precision_recall_curve(y_test.ravel(),y_score.ravel())

average_precision['micro'] = average_precision_score(y_test, y_score, average='micro')

plt.clf()# 清楚当前图像窗口
plt.plot(recall['micro'],precision['micro'],label='micro-average Precision-recall curve (area ={0:0.2f})'.format(average_precision['micro']))

[]

for i in range(n_classes):
    plt.plot(recall[i], precision[i], label='Precision recall curve of class {0} (area = {1:0.2f})'.format(i,average_precision[i]))

#调整刻度范围 
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.05])
# 横纵坐标
plt.xlabel('Recall',fontsize=16)
plt.ylabel('Precision',fontsize=16)
# 图像名称 图例
plt.title('Extension of Precision-Recall curve to multi-class',fontsize=16)
plt.legend(loc="lower right")
plt.show()