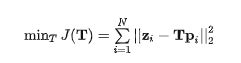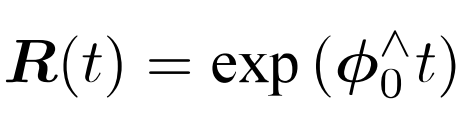SLAM14讲 01

欧式变换：

在欧式变换前后的两个坐标系下,同一个向量的模长和方向不发生改变,是为欧式变换.

一个欧式变换由一个旋转和一个平移组成。

齐次坐标

齐次坐标：将n维的向量用n+1维向量表示，我们常用在3维向量末尾添加1变成4维的齐次坐标。

引入齐次坐标的目的是合并矩阵运算中的加法和乘法。

在齐次坐标中，某个点p的每个分量同乘以一个非0常数w，仍然表示3维空间中同一个点。

齐次坐标(Xc , Yc , Zc ,1)T 对应3维空间的点为(Xc , Yc , Zc)T 。

如下所示：

为什么要用到李群和李代数？

避免一直是数学上的推导。

假设某个时刻我们预测机器人的位姿为 T （待定值）, 它观测到了一个惯性坐标系下的点 p 而产生了一个观测数据 z ，它是该点在相机坐标系下的坐标，则可得

z=Tp+ω

其中， ω 是观测噪声。由于观测噪声的存在， z 无法严格满足式 z=Tp。因此而产生的误差 e 为

e=z−Tp

若共有N 个观测值，那么就有N 个这样的式子。机器人的位姿估计就转变成寻找一个最优的 T 使得整体的误差最小化：

 通常，直接求解上式得出最优的 T 是很困难的（或计算量很大）。我们常常先给定一个猜测值（初始值） T0 ，然后不断地对它进行迭代更新。而这个过程需要用到导数（可以想想梯度下降法）。回顾导数的定义

 显然计算导数和进行更新时都要用到加法。但SO(3) 和SE(3) 上对矩阵加法的运算并不封闭。如果要继续采取这个迭代更新的策略势必要再想想办法，使得导数“可行”。而这就可以通过李群及其对应的李代数来实现。

参考：https://zhuanlan.zhihu.com/p/33156814

角点

角点是图像很重要的特征，某方面属性特别突出的点，是在某些属性上强度最大或者最小的孤立点、线段的终点等。对图像图形的理解和分析有很重要的作用。角点在保留图像图形重要特征的同时,可以有效地减少信息的数据量，使其信息的含量很高，有效地提高了计算的速度,有利于图像的可靠匹配,使得实时处理成为可能。

 图参考：https://blog.csdn.net/weixin_41809077/article/details/125466380

李群与李代数

R在原点附近的一阶泰勒展开，我们看到这个向量φ=（φ1，φ2，φ3）反应了R的导数性质，故称它在SO(3)上的原点 φ0 附近的正切空间上。这个φ正是李群大SO(3)对应的李代数小so(3)

李代数小so(3)是三维向量φ的集合，每个向量φi的反对称矩阵都可以表达李群(大SO(3))上旋转矩阵R的导数，而R和φ是一个指数映射关系。也就是说，李群空间的任意一个旋转矩阵R都可以用李代数空间的一个向量的反对称矩阵指数来近似

泰勒公式：

参考：https://mp.weixin.qq.com/s/sVjy9kr-8qc9W9VN78JoDQ

状态估计

我们已知的是：运动方程、观测方程、运动数据、图片数据；
我们求解目标的是：相机各个时刻的位姿和路标点的世界坐标。
概括起来就是：在已知SLAM模型的情况下，通过带噪声的数据z和u推断位姿x和地图y的概率分布，这是一个状态估计问题。
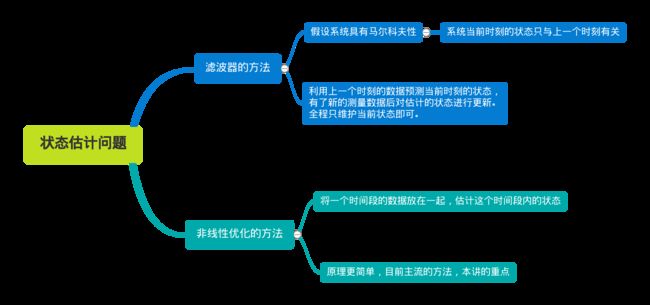
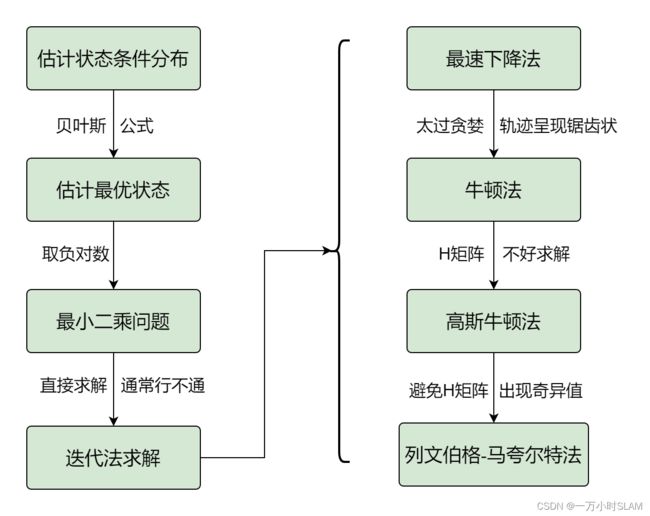
状态估计问题如何求解呢？

 

 

参考：https://blog.csdn.net/weixin_42126210/article/details/123648742