自适应OCXO漂移校正算法（翻译）

原作者：C.W.T.Nicholls and G.C.Carleton, Nortel Networks, Wireless Technology Laboratory, Canada

摘要

本文提出了一种在CDMA cellular radio system中实现的算法，使基站时间参考振荡器的稳定性要去降低了5倍。该算法自适应地对CDMA基站时间参考OCXO的频率漂移特性进行建模，同时锁定到具有50ppb/scc的1σ抖动的1pps卫星时间参考信号。由该算法生成的OCXO模型在卫星时间基准丢失的情况下被使用，以在长达24小时的保持期内提供基站基准振荡器的时间校正，在此期间进行卫星时间基准信号的修复或重新获取。
该算法的新颖之处在于使用两个并行卡尔曼滤波器自适应地对OCXO的温度和老化相关的频率稳定性进行建模。该算法提取了OCXO相对于噪声1pps卫星时间基准的0.4ppb/75C和0.05ppb/24hours的稳定性相关性。卡尔曼滤波器模型的自适应训练发生在卫星能见度丢失之前，并在重新获得卫星时间基准之后重新开始。以这种方式，算法认识到产品寿命期间OCXO频率稳定性特征的变化。在保持期间，卡尔曼滤波器作为预测状态机工作，根据自适应模型的训练系数为基站OCXO时间基准产生校正信号。
该校正算法已经在CDMA基站网络中进行了试验，并被证明在24小时的保持期内将10MHz定时模块参考振荡器保持在CDMA系统时间的1.5us以内，这在8小时的保持期内完全符合10us的3GPP2 CDMA标准累积时间误差规范。仿真表明，该算法能够补偿基准振荡器稳定性进一步降低10倍的情况，同时仍能满足8小时保持时间的要求。

介绍

3GPP2推荐的cdma2000扩频 基站最低性能标准要求基站在没有外部频率参考（称为保持）的情况下，将时间校准保持在CDMA系统时间的10us以内，持续时间不少于8小时。此外，基站参考振荡器的最大频率误差不能超过50ppb。使用该算法 的系统设计要求在8小时的指定保持期和24小时的目标保持期内满足更严格的时间误差规格6.921us。在目前的工作中，1pps时间基准是从俄罗斯卫星系统GLONASS提取的，该系统使用原子频率标准来确保5.10^-4ppb/day的频率稳定性。GLONASS信号是使用科特林K161双模接收机检测的。开发的定时模块也与GPS卫星系统兼容。参考文献【2】中提供了GLONASS和GPS全球定位系统时间链路性能的比较。
在保持周期期间可以容忍的解锁基站时间基准中的最大静态频率稳定性误差可以通过将以秒为单位的累积时间误差除以以秒为单位的保持持续时间来估计，如等式（1）所示。

表1列出了8小时和24小时保持期情况下保持期间允许的最大静态频率稳定性偏移。

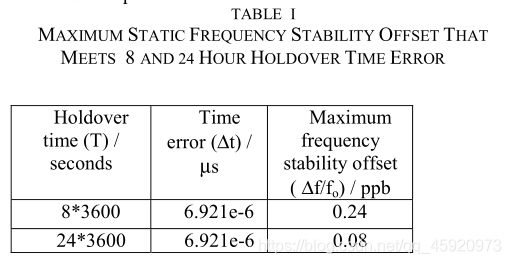
应当注意，振荡器频率稳定性在保持期间的变化可能超过表1给出的数字，但是，如果保持时间内稳定性变化的积分在规定的累积时间误差内，并且不超过50ppb的最大频率精度规格，则继续满足CDMA2000规格。
本定时模块所设计的室内基站的工作温度范围为-5℃至+50℃。室外基站的设计运行环境温度为-5℃至+70℃。能够满足表1中稳定性要求的参考振荡器超过了时序模块的成本目标。
在本文中，当外部时序基准不可用时，通过使用自适应振荡器模型来校正振荡器，降低了基准振荡器的稳定性要求。晶体振荡器老化的自适应模型的结果已经发表，这些模型不同于目前的工作，因为它们考虑了在几个月和几年的时间周期内的预测，而目前的工作集中在相对短的8和24小时的保持周期内的精确预测。
本文使用线性自适应振荡器模型（AOM）来表征频率稳定性的温度依赖性。基于环境温度和振荡器频率稳定性之间的线性关系，线性近似是合理的，振荡器频率稳定性是由振荡器晶体温度的烘箱控制产生的。老化过程的线性建模也优于已发表作品的对数模型，因为模型必须精确的保持期相对于老化特性的非线性引入所需时间精度的显著误差所需的时间间隔较短。
当参考振荡器被锁定到卫星时间信号时，AOM连续地适应振荡器频率稳定特性。在卫星参考信号丢失地情况下，该模型用于校正本地振荡器。该模型基于卡尔曼滤波器，用于在卫星锁定条件下跟踪振荡器状态地最佳估计，并在失去锁定的情况下自传播模型解，以便在保持期间预测校正振荡器。
第二节介绍了定时模块中使用的基准振荡器的老化和温度对频率的依赖性。第三节描述了数字锁相环的操作，第四节介绍了自适应振荡器模型构架。第五节和第六节提供了用于对振荡器老化和温度特性建模的卡尔曼滤波器的数学背景。第七节讨论了预测模型的仿真结果，第八节给出了在CDMA系统定时模块中运行的自适应算法的测量性能数据。

参考振荡器

定时模块使用TEMEX、10MHz、SC cut、double oven crystal oscillator、DOC 4397，其频率稳定性随温度的变化为0.4ppb/75degrees Celsius，连续运行4周后的老化规格为0.05ppb/24hours。给出了在生产就绪时序模块上24小时保持测试运行的结果，结果表明保持期间补偿参考振荡器时间误差变化减少了10倍以上，整个24小时期间的最大累积时间误差-1.5us 。这些结果表明，相对于0.08ppb的静态频率稳定性偏移，耐热晶体振荡器的稳定性拜年话规格增加了5倍，可以通过开发的算法进行补偿。

数字锁相环

图1显示了用于将参考振荡器锁相到卫星时间参考的数字锁相环（DPLL）和AOM（自适应振荡器模型）。AOM和DPLL并行运行，使用校正信号和参考振荡器环境温度来训练自适应模型。OCXO的环境温度使用Maxim DS18B20车载温度传感器测量，精度为+/-0.5℃。温度传感器位于OCXO附近，位于基站冷却风扇产生的气流中。

DPLL具有1Hz的更新速率，并且将基站定时模块的10MHz晶体振荡器锁定到GLONASS导出的1pps信号。GLONASS接收机模块在接收的1pps时间基准上引入约~ 50ns/s的1σ边沿抖动。在产生数字校正信号之前，控制环路将1σ边沿抖动降至约0.33ns/s。数字校正信号被施加到一个20位的Burr Brown DAC1220，该转化器产生一个0到5V范围内的控制电压，用于通过电子频率控制（EFC）端口控制OCXO。OCXO的标称调谐灵敏度为200ppb/Vconsequently，因此DPLL的标称校正分辨率为5/(2^20)*200ppb/bit 或 0.001ppb/bit。
DPLL使用的相位检测器是在Alterra EP20K160 FPGA中实现的。鉴相器使用160MHz时钟，该时钟由10MHz片上基准电压源合成，可提供6.25ns的分辨率精度，即GLONASS接收器模块产生的1pps与OCXO产生的内部1pps之间的时间误差。数字鉴相器的输出被反馈回嵌入在FPGA中的32位Nios处理器。Nios处理器包含信号处理算法和自适应算法，信号处理算法计算反馈到数模转换器的控制信号。这些算法是使用Matlab v6.5开发的，在编译并加载到Nios处理器之前，先转换为C++语言。
数字鉴相器的输出将相位误差表示为160MHz的时钟周期数。控制算法的第一个操作是将DPD输出的周期数乘以160MHz时钟（6.25ns）的周期，以获得时间误差。第二个操作是乘以第二时间误差的积分用于产生CTE（累积时间误差）。振荡器控制信号中的CTE的使用确保了过去的时间误差被考虑在内。计算校正信号（见等式1），从校正信号的2000点移动平均值中减去CTE除以150的阻尼系数。阻尼因子使校正信号对GLONASS接收机引入的50ns/s随机相位误差的敏感度降低150倍，因此应用于参考振荡器的校正包含0.33ns/s的1σ噪声分量。在初始锁相和从保持状态恢复期间，阻尼值设置为单位值，以最小化环路的拉入时间。一旦CTE降至200ns以下，阻尼因子设置为150，以在卫星接收器噪声抑制和振荡器稳定性漂移跟踪之间提供最佳折衷。（1）的参考校正值保持基于过去2000个校正值的校正信号的稳定值。应用CTE的变化来相对于参考校正值控制振荡器。在应用数模转换器之前，校正值限制在45ppb，以满足CDMA2000 50ppb频率精度规格。总之，时间误差导致参考振荡器频率的调整，以减慢定时模块时钟或加快其速度来消除检测到的时间误差。

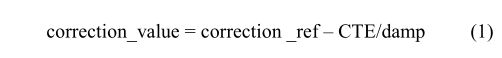
数模转换器步长的计算方法是用OCXO调谐灵敏度的校准值除以以ppb/V为单位的校正值，得到一个电压。调谐电压除以数模转换器的控制电压范围，提供了可应用的数模转换器步骤总数的一小部分。然后，通过将数模转换器步骤总数乘以所需总范围的分数，来计算表示校正值所需的数模转换器步骤数。
当锁定到卫星参考时，数模转换器开关被设置到校正信号计算器模块的输出，并且校正值和温度作为训练信号被应用到AOM。从锁定模式转换到保持模式时，数模转换器输入开关选择AOM输出或代表过去100个校正值移动平均值的平均校正值。关于选择哪一个输入的决定是基于训练定时器输出，该输出指示AOM是否已经完成了其完整的2小时训练周期。在训练周期已经完成的情况下，选择AOM并作为预测状态机操作，基于温度传感器输入和振荡器的训练模型提供预测校正信号。

自适应振荡器模型

图2是AOM的框图。DPLL在通电30分钟后关闭，以避免OCXO频率稳定性的预热瞬变，该瞬变落在DPLL标称+/-500ppb范围之外。就在DPLL关闭之前，通过数模转换器向OCXO施加50ppb的阶跃，以校准OCXO的调谐灵敏度，称为Kvco。应用50ppb步长前后DPD输出的100点移动平均值的差值除以数模转换器施加的已知电压，以提供Kvco的校准值。Kvco校准使DPLL能够抵抗OCXO调谐灵敏度的逐部变化。相对于DPLL闭合，AOM算法将模型的训练延迟了9个小时，以确保由环路闭合、烘箱稳定和晶体回归引起的频率稳定性瞬变相对于依赖于温度和老化的稳定性而言是二阶的。9小时的训练延迟期之后是2小时的连续训练期，在此期间模型精度收敛到满足保持时间误差规格6.921us所需的精度。两个小时的训练期结束后，自适应模型继续训练，同时系统锁定在卫星基准上，并用于在保持的情况下校正振荡器漂移特性。对于CDMA系统规范而言，9小时的训练延迟和2小时的训练周期是可以接受的，该规范允许定时模块在被基站使用之前有48小时来进行任何训练和稳定。

三个无限脉冲响应滤波器（IIRF）用于AOM，以降低校正信号中的接收机噪声，并能够分离温度和老化相关的频率稳定性。IIRF1和IIRF3的瞬态响应时间为3.47小时，IIRF2的瞬态响应时间为7.2天。滤波器的长瞬态响应需要防止由OCXO的初始锁相产生的校正信号的阶跃瞬态进入滤波器。DPLL关闭9小时后，通过减去AOM训练开始时的校正信号值来消除阶跃瞬态。因此，应用于AOM的校正信号值从零值开始。从校正信号中减去的初始校正值被加到AOM输出端的预测校正信号上，确保AOM的预测校正是在锁相条件下应用的校正信号的真实反映。
IIR滤波器的递归特性能够实现窄带宽，而不需要等效有限脉冲响应滤波器所需的大内存存储。IIRF1是一个单极滤波器，其带宽设计为通过由振荡器频率稳定性对温度的依赖性导致的校正信号的最高变化率。定时模块被指定以10oC/hour的最高温度斜坡运行。对于0.4ppb/75oC的OCXO，假设稳定性与温度呈线性关系，这导致由1.48x10^-5ppb/s。温度斜坡引起的稳定性的最大变化率。

适应性老化模型

自适应温度模型

仿真算法性能

测量算法性能

结论

致谢

参考文献

[1] Y.Gouzhva, A.Gevorkyan, P.Bogdanov, “Accuracy Estimation of
Glonass satellite oscillators”, 1992 IEEE Frequency Control Symposium.
[2]W.Lewandowski, J.Danaher and W.J.Klepczynski, “GLONASS
Common-View time transfer between North America and Europe and its
comparison with GPS,” European Frequency Time Forum, 5-7 March 1996
Conference Publication, No 418.
[3] Y.Shmaliy, A.Marienko, A.Savchuk, “GPS-based optimal kalman
estimation of time error, frequency offset and aging”’ 31st A n n u a l P r e c i s e
Time and Time Interval (PTTI) Meeting, pp 431-440.
[4]S.Stein, “Kalman Filter Analysis of precision clocks with real time
parameter estimation,” 43rd Annual Symposium on Frequency Control 1989.
[5] W.Su and R.Filler, “Application of Kalman filtering techniques to the
precision clock with non constant aging,” 1992 IEEE Frequency Control
Symposium.
[6] W.Su and R.Filler, “A new approach to clock modeling and kalamn filter
time frequency prediction,” 1993 IEEE International Frequency Control
Symposium.
[7]S.R.Stein and R.L.Filler, “Kalman Filter Analysis for real time
applications of clocks and oscillators,” 42nd A n n u a l F r e q u e n c y C o n t r o l
Symposium 1988.
[8] R.E.Kalman “A New Approach to linear Filtering and Prediction
Problems,” Trans. Of the ASME-J. of Basic Engr. , pp.33-45, March 1960.
[9]R. G. Brown and P. Y.C.Hwang, “Introduction to Random Signals and
Applied Kalman Filtering,” John Wiley & Sons, Inc., ISBN 0471-52573-1,
1983.
[10]D.Simon, “Kalman Filtering,” Embedded Systems Programming, June
2001, pp72-79.