Python计算机视觉——图像内容分类
文章目录
- 第八章 图像内容分类
-
- (一)K邻近分类法(KNN)
- (二)贝叶斯分类器
- (三)支持向量机
- (四)光学字符识别
第八章 图像内容分类
本章介绍图像分类和图像内容分类算法。
先介绍一些简单而有效的方法和一些性能最好的分类器,运用它们解决两类和多类分类问题,再展示两个用于手势识别和目标识别的应用实例。
(一)K邻近分类法(KNN)
在分类方法中,最简单且用的最多的一种方法之一是KNN。
这种方法把要分类的对象(例如一个特征向量)与训练集中已知类标记的所有对象进行对比,并由k近邻对指派到哪个类进行投票。
缺点:需要预先设定k值,k值得选择会影响分类得性能;这种方法要求将整个训练集存储起来,如果训练集非常大,搜索起来就非常慢;可并行性一般
优点:这种方法在采用何种距离度量方面没有限制
实现最基本的KNN形式:给定训练样本集和对应的标记列表,这些训练样本和标记可以在一个数组里成行摆放或者干脆摆放到列表里,训练样本可能是数字、字符串等任何形状。将定义的对象添加到名为knn.py的文件里。(此处采用的是欧氏距离进行度量)
一个简单的二维示例
首先建立一些简单的二维示例数据集来说明并可视化分类器的工作原理。
下面的脚本将创建两个不同的二维点集,每个点集有两类,用Pickle模块来保存创建的数据。我们需要四个二维数据集文件,每个分布都有两个文件,一个用来训练,另一个用来做测试。
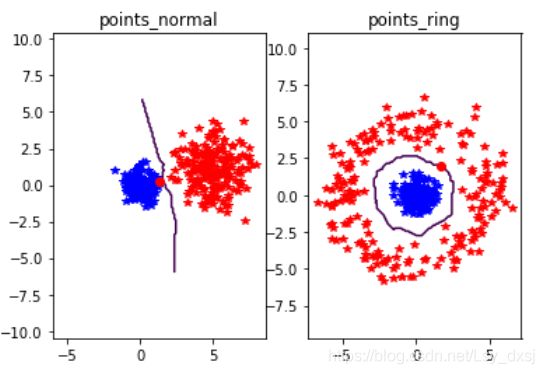
如图中所示:
先用Pickle模块创建一个KNN分类器模型,再载入另一个数据集(测试数据集),并在控制台上打印第一个数据点估计出来的类标记。为了可视化所有测试数据点的分类,并展示分类器将两个不同的类分开的怎么样,可以创建一个简短的辅助函数以获取x和y二维坐标数组和分类器,并返回一个预测的类标记数组。
绘制出的结果如下图所示:
可以看到,KNN决策边界适用于没有任何明确模型的类分布
代码为:
# -*- coding: utf-8 -*-
from numpy.random import randn
import pickle
from pylab import *
# create sample data of 2D points
n = 200
# two normal distributions
class_1 = 0.6 * randn(n,2)
class_2 = 1.2 * randn(n,2) + array([5,1])
labels = hstack((ones(n),-ones(n)))
# save with Pickle
#with open('points_normal.pkl', 'w') as f:
with open('points_normal.pkl', 'wb') as f:
pickle.dump(class_1,f)
pickle.dump(class_2,f)
pickle.dump(labels,f)
# normal distribution and ring around it
class_1 = 0.6 * randn(n,2)
r = 0.8 * randn(n,1) + 5
angle = 2*pi * randn(n,1)
class_2 = hstack((r*cos(angle),r*sin(angle)))
labels = hstack((ones(n),-ones(n)))
# save with Pickle
#with open('points_ring.pkl', 'w') as f:
with open('points_ring.pkl', 'wb') as f:
pickle.dump(class_1,f)
pickle.dump(class_2,f)
pickle.dump(labels,f)
# -*- coding: utf-8 -*-
import pickle
from pylab import *
import knn
import imtools
pklist=['points_normal.pkl','points_ring.pkl']
figure()
# load 2D points using Pickle
for i, pklfile in enumerate(pklist):
with open(pklfile, 'rb') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
# load test data using Pickle
with open(pklfile[:-4]+'_test.pkl', 'rb') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
model = knn.KnnClassifier(labels,vstack((class_1,class_2)))
# test on the first point
print(model.classify(class_1[0]))
#define function for plotting
def classify(x,y,model=model):
return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])
# lot the classification boundary
subplot(1,2,i+1)
imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
titlename=pklfile[:-4]
title(titlename)
show()
用稠密SIFT作为图像特征
上一节是对点进行分类,这一节学习如何对图像进行分类。
要对图像进行分类,需要一个特征向量来表示一幅图像,这节学的是稠密SIFT特征向量。
创建名为dsift.py文件,将帧数组存储在一个文本文件中。例如用下面的代码来计算稠密SIFT描述子,并可视化它们的位置:
# -*- coding: utf-8 -*-
import sift, dsift
from pylab import *
from PIL import Image
dsift.process_image_dsift('empire.jpg','empire.dsift',90,40,True)
l,d = sift.read_features_from_file('empire.dsift')
im = array(Image.open('empire.jpg'))
sift.plot_features(im,l,True)
title('dense SIFT')
show()
得到的结果为:
图像分类:手势识别
在此应用中,我们使用稠密SIFT描述子来表示这些收拾图像,并建立一个简单的手势识别系统。
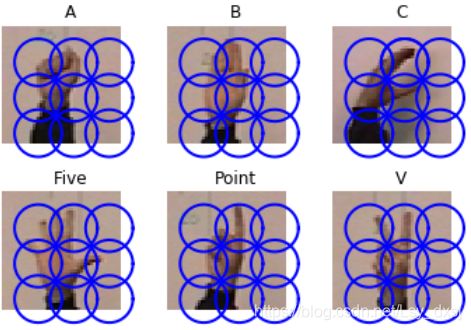
我们使用静态手势数据库中的一些图像进行演示。
如下图所示:
代码为:
# -*- coding: utf-8 -*-
import os
import sift, dsift
from pylab import *
from PIL import Image
imlist=['train/A-uniform01.ppm','train/B-uniform01.ppm',
'train/C-uniform02.ppm','train/Five-uniform01.ppm',
'train/Point-uniform01.ppm','train/V-uniform01.ppm']
figure()
for i, im in enumerate(imlist):
dsift.process_image_dsift(im,im[:-3]+'dsift',30,15,True)
l,d = sift.read_features_from_file(im[:-3]+'dsift')
dirpath, filename=os.path.split(im)
im = array(Image.open(im))
#显示手势含义title
titlename=filename[:-14]
subplot(2,3,i+1)
sift.plot_features(im,l,True)
title(titlename)
show()
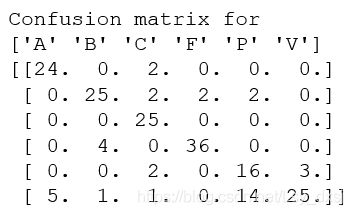
得到的准确率和混淆矩阵为:
说明该例中有81%的图像是正确的,混淆矩阵可以显示每类有多少个样本被分在每一类中的矩阵,它可以显示错误的分布情况,以及哪些类是经常“混淆”的。
代码为:
#得到每幅图的稠密sift特征
import dsift
# 将图像尺寸调为 (50,50),然后进行处理
for filename in imlist:
featfile = filename[:-3]+'dsift'
dsift.process_image_dsift(filename,featfile,10,5,resize=(50,50))
#辅助函数,用于从文件中读取稠密SIFT描述子
import os
import sift
def read_gesture_features_labels(path):
# create list of all files ending in .dsift
featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
# read the features
features = []
for featfile in featlist:
l,d = sift.read_features_from_file(featfile)
features.append(d.flatten())
features = array(features)
# create labels
labels = [featfile.split('/')[-1][0] for featfile in featlist]
return features,array(labels)
#读取训练集、测试集的特征和标记信息
features,labels = read_gesture_features_labels('gesture/train/')
test_features,test_labels = read_gesture_features_labels('gesture/test/')
classnames = unique(labels)
#使用过前面的K近邻代码
# test kNN
import knn
k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in range(len(test_labels))])
# accuracy
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print('Accuracy:', acc)
#打印标记及相应的混淆矩阵
def print_confusion(res,labels,classnames):
n = len(classnames)
# confusion matrix
class_ind = dict([(classnames[i],i) for i in range(n)])
confuse = zeros((n,n))
for i in range(len(test_labels)):
confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
print('Confusion matrix for')
print(classnames)
print(confuse)
print_confusion(res,test_labels,classnames)
(二)贝叶斯分类器
另一个简单而有效的分类器是贝叶斯分类器(或称朴素贝叶斯分类器),它是一种基于贝叶斯条件概率定理的概率分类器,它假设特征是彼此独立不相关的。一旦学习了这个模型,就没有必要存储训练数据,只需存储模型的参数。
原理:该分类器是通过将各个特征的条件概率相乘得到一个类的总概率,然后选取概率最高的那个类构造出来的。
实例:创建名为bayes.py的文件,添加Classifier类。该模型每一类都有两个变量,类均值和协方差。将该贝叶斯分类器用于上一节的二维数据,下面的脚本载入上一节的二维数据,并训练出一个分类器:
import pickle
import bayes
import imtools
# 用 Pickle 模块载入二维样本点
with open('points_normal.pkl', 'rb') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
# 训练贝叶斯分类器
bc = bayes.BayesClassifier()
bc.train([class_1,class_2],[1,-1])
载入上一节中的二维测试数据对分类器进行测试:
import pickle
import bayes
import imtools
# 用 Pickle 模块载入二维样本点
with open('points_normal.pkl', 'rb') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
# 训练贝叶斯分类器
bc = bayes.BayesClassifier()
bc.train([class_1,class_2],[1,-1])
该脚本将前10个二维数据点的分类结果打印输出到控制台,结果为:
![]()
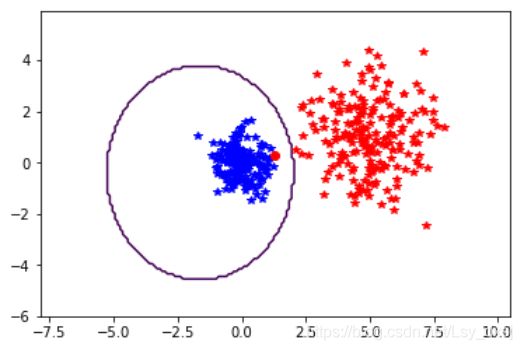
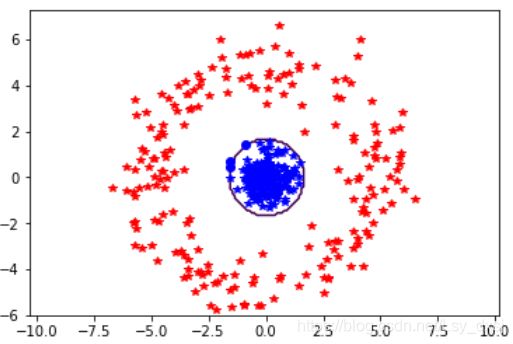
两个数据集的分类结果如下图所示:
该例中,决策边界是一个椭圆,类似于二维高斯函数的等值线。
接下来尝试手势识别问题。由于稠密SIFT描述子的特征向量十分庞大,所以在数据拟合模型之前需要进行降维处理,此时,采用PCA(主成分分析)来降维。创建名为pca.py的文件。
在本例中,我们在训练数据上用PCA降维,并保持在这50维具有最大的方差。
#辅助函数,用于从文件中读取稠密SIFT描述子
import os
import sift
from numpy import *
def read_gesture_features_labels(path):
# create list of all files ending in .dsift
featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
# read the features
features = []
for featfile in featlist:
l,d = sift.read_features_from_file(featfile)
features.append(d.flatten())
features = array(features)
# create labels
labels = [featfile.split('/')[-1][0] for featfile in featlist]
return features,array(labels)
#读取训练集、测试集的特征和标记信息
features,labels = read_gesture_features_labels('gesture/train/')
test_features,test_labels = read_gesture_features_labels('gesture/test/')
classnames = unique(labels)
# PCA降维
import pca
V,S,m = pca.pca(features)
# 保持最重要的成分
V = V[:50]
features = array([dot(V,f-m) for f in features])
test_features = array([dot(V,f-m) for f in test_features])
训练并测试贝叶斯分类器如下:
import bayes
# 测试贝叶斯分类器
bc = bayes.BayesClassifier()
blist = [features[where(labels==c)[0]] for c in classnames]
bc.train(blist,classnames)
res = bc.classify(test_features)[0]
检查分类准确率:
import knn
k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in range(len(test_labels))])
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print('Accuracy:', acc)
输出为:
检查混淆矩阵:
#打印标记及相应的混淆矩阵
def print_confusion(res,labels,classnames):
n = len(classnames)
# confusion matrix
class_ind = dict([(classnames[i],i) for i in range(n)])
confuse = zeros((n,n))
for i in range(len(test_labels)):
confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
print('Confusion matrix for')
print(classnames)
print(confuse)
print_confusion(res,test_labels,classnames)
输出结果为:
虽然分类效果不如K近邻分类器,但贝叶斯分类器不需要保存任何训练数据,而且只需保存每个类的模型参数。
(三)支持向量机
支持向量机(SVM)是一类强大的分类器,可以在很多分类问题中给出现有水准很高的分类结果。
方法:最简单的SVM通过在高维空间中寻找一个最优线性分类面,尽可能地将两类数据分开。
对于一特征向量x的决策函数为:
f ( x ) = w ⋅ x − b f(x)=w·x-b f(x)=w⋅x−b
其中w是常规的超平面,b是偏移量常数。
可以写成:
f ( x ) = ∑ i α i y i x i ⋅ x − b f(x)=\sum_{i} \alpha_{i} y_{i} \boldsymbol{x}_{i} \cdot \boldsymbol{x}-b f(x)=i∑αiyixi⋅x−b
这里的i是从训练集中选出的部分样本,这里选择的样本称为支持向量,因为它们
可以帮助定义分类的边界
优点:可以使用核函数。核函数能够将特征向量映射到另外一个不同维度的空间中,比如高维度空间。通过核函数映射,依然可以保持对决策函数的控制,从而可以有效地解决非线性或者很难的分类问题。
最常见的核函数:
线性是最简单的情况,即在特征空间中的超平面是线性的, K ( x i , x ) = x i ⋅ x K\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)=\boldsymbol{x}_{i} \cdot \boldsymbol{x} K(xi,x)=xi⋅x;
多项式用次数为 d 的多项式对特征进行映射, K ( x i , x ) = ( γ x i ⋅ x + r ) d , γ > 0 K\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)=\left(\gamma \boldsymbol{x}_{i} \cdot \boldsymbol{x}+r\right)^{d}, \quad \gamma>0 K(xi,x)=(γxi⋅x+r)d,γ>0;
径向基函数,通常指数函数是一种极其有效的选择, K ( x i , x ) = e ( − γ ∣ ∣ x i − x ∥ 2 ) , γ > 0 K\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)=\mathrm{e}^{\left(-\gamma|| \boldsymbol{x}_{i}-x \|^{2}\right)}, \quad \gamma>0 K(xi,x)=e(−γ∣∣xi−x∥2),γ>0
Sigmoid 函数,一个更光滑的超平面替代方案, K ( x i , x ) = tanh ( γ x i ⋅ x + r ) K\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)=\tanh \left(\gamma \boldsymbol{x}_{i} \cdot \boldsymbol{x}+r\right) K(xi,x)=tanh(γxi⋅x+r)。
每个核函数的参数都是在训练阶段确定的
使用LibSVM
LibSVM下载地址:http://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html#download
LibSVM载入在前面KNN范例分类中用到的数据点,并用径向基函数训练一个SVM分类器:
import pickle
from svmutil import *
import imtools
# 用 Pickle 载入二维样本点
with open('points_ring.pkl', 'rb') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
# 转换成列表,便于使用 libSVM
class_1 = list(map(list,class_1))
class_2 = list(map(list,class_2))
labels = list(labels)
samples = class_1+class_2 # 连接两个列表
# 创建 SVM
prob = svm_problem(labels,samples)
param = svm_parameter('-t 2')
# 在数据上训练 SVM
m = svm_train(prob,param)
# 在训练数据上分类效果如何?
res = svm_predict(labels,samples,m)
打印输出结果如下:
![]()
现在,载入其他数据集,并对该分类器进行测试:
# 用 Pickle 模块载入测试数据
with open('points_normal_test.pkl', 'r') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
# 转换成列表,便于使用 LibSVM
class_1 = map(list,class_1)
class_2 = map(list,class_2)
# 定义绘图函数
def predict(x,y,model=m):
return array(svm_predict([0]*len(x),zip(x,y),model)[0])
# 绘制分类边界
imtools.plot_2D_boundary([-6,6,-6,6],[array(class_1),array(class_2)],predict,[-1,1])
show()
(四)光学字符识别
光学字符识别(OCR)是一个多类问题实例,是一个理解手写或机写文本图像的处理过程。常见的例子是通过扫描文件来提取文本。本节主要理解数度图像。
流程:我们假设数独图像是已经对齐的,其水平和垂直网格线平行于图像的边,在这些条件下,可以对图像进行阈值处理,并在水平和垂直方向上分别对像素值求和由于这些经阈值处理的边界值为 1,而其他部分值为 0,所以这些边界处会给出很强的响应,可以告诉我们从何处进行裁剪。
# -*- coding: utf-8 -*-
from PIL import Image
from pylab import *
from scipy.ndimage import measurements
def find_sudoku_edges(im, axis=0):
""" 寻找对齐后数独图像的的单元边线 """
# threshold and sum rows and columns
#阈值化,像素值小于128的阈值处理后为1,大于128的为0
trim = 1*(128 > im)
#阈值处理后对行(列)相加求和
s = trim.sum(axis=axis)
# print(s)
# find center of strongest lines
# 寻找连通区域
s_labels, s_nbr = measurements.label((0.5*max(s)) < s)
# print(s_labels)
# print(s_nbr)
#计算各连通域的质心
m = measurements.center_of_mass(s, s_labels, range(1, s_nbr+1))
# print(m)
#对质心取整,质心即为粗线条所在位置
x = [int(x[0]) for x in m]
# print(x)
# if only the strong lines are detected add lines in between
# 如果检测到了粗线条,便在粗线条间添加直线
if 4 == len(x):
dx = diff(x)
x = [x[0], x[0]+dx[0]/3, x[0]+2*dx[0]/3, x[1], x[1]+dx[1]/3, x[1]+2*dx[1]/3, x[2], x[2]+dx[2]/3, x[2]+2*dx[2]/3, x[3]]
if 10 == len(x):
return x
else:
raise RuntimeError('Edges not detected.')
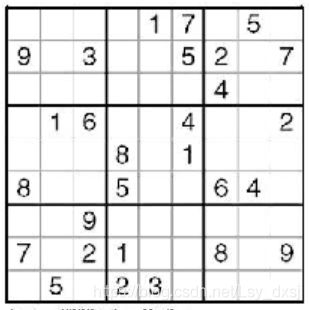
接下来输入原图:
imname = '2.png'
im = array(Image.open(imname).convert('L'))
print(im.shape)
figure()
gray()
imshow(im)
axis('off')
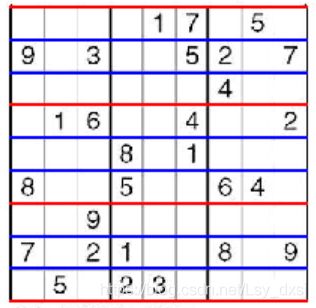
得到单元边界线,并进行绘制输出
# find the cell edges
# 寻找x方向的单元边线
x = find_sudoku_edges(im, axis=0)
#寻找y方向的单元边线
y = find_sudoku_edges(im, axis=1)
figure()
gray()
y1=[y[0],y[3],y[6],y[-1]]
y2=[y[1],y[2],y[4],y[5],y[7],y[8]]
#画直线
for i, ch in enumerate(y1):
x1 = range(x[0], x[-1]+1, 1)
y1 = ch*ones(len(x1))
#画散点图
plot(x1, y1, 'r', linewidth=2)
for i, ch in enumerate(y2):
x1 = range(x[0], x[-1]+1, 1)
y1 = ch*ones(len(x1))
#画散点图
plot(x1, y1, 'b', linewidth=2)
'''for i, ch in enumerate(x):
y1 = range(x[0], x[-1]+1, 1)
x1 = ch*ones(len(x1))
#画散点图
plot(x1, y1, 'r', linewidth=2)
plot(x, y, 'or', linewidth=2)'''
imshow(im)
axis('off')
show()