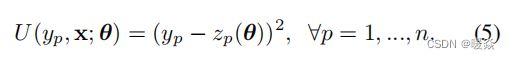【论文精读】从单张图像进行深度估计的深度卷积神经场

Paper Information

论文： Deep convolutional neural fields for depth estimation from a single image.F. Liu, C. Shen, G. Lin. Proc. IEEE Conference on Computer Vision and Pattern Recognition (CVPR’15), 2015.
相关：Learning depth from single monocular images using deep convolutional neural fields, F. Liu, C. Shen, G. Lin, I. Reid. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 2016.
注意：除非另有说明，否则本篇论文使用粗体大写和小写字母分别表示矩阵和列向量。
参考：论文笔记_S2D. 34-2015-CVPR_从单张图像进行深度估计的深度卷积神经场 - 惊鸿一博
参考：论文笔记_S2D.37-2015-TPAMI_使用深度卷积神经场从单目图像学习深度 - 惊鸿一博

Abstract

我们在这项工作中考虑了从单张单目图像进行深度估计的问题。由于没有可靠的深度线索，例如立声对应关系，运动等，因此这是一项艰巨的任务。以前的工作一直集中在利用几何先验或其他信息源上，而所有这些都使用手工制作的功能。最近，越来越多的证据表明，深度卷积神经网络（CNN）的功能正在为各种视觉应用创造新记录。另一方面，考虑到深度值的连续特性，深度估计自然可以公式化为连续条件随机场（CRF）学习问题。因此，我们在本文中提出了一种深度卷积神经场模型，用于从单张图像估计深度，旨在共同探索深层CNN和连续CRF的能力。具体来说，我们提出了一种深度结构化的学习方案，该方案可以在统一的深度CNN框架中学习连续CRF的一元势函数和二元势函数（the unary and pairwise potentials）。

随机场（Random Field）：随机场可被看成是随机过程一般化(Generalization)的产物，随机过程的参数通常是时间/次数等1维结构，如伯努利过程(Bernoulli process)是个二值Binary（0/1）的随机变量序列，连续抛硬币是典型的伯努利过程；而随机场的参数通常是多维向量或是位于某流形（Manifold）上点等多维结构。随机场和随机过程的差异也常被模糊化，当希望强调参数空间的几何结构（多维）时，使用“随机场”，当参数是时间维度（1维）时，使用“随机过程”。常见的随机场包括MRF，Gibbs随机场，CRF和高斯随机场等。
条件随机场（Conditional Random Field，CRF）：模式识别/机器学习中一种较常见的概率图模型（Probabilistic Graph Model，PGM）方法，适合对上下文相关的样本间存在依赖关系的情况建模，机器学习分类算法在预测样本标签时通常不会考虑“相邻”样本的情况（如逻辑回归等），在一些上下文相关的场景中，完全忽略周围环境的影响难以产生最优的结果。在计算机视觉（CV）的语义分割中，临近的像素属于同一类别的可能性较高，通常位置/颜色/语义等属性相似的像素的属于同一类的可能性较高；目标识别中，连续帧的图像具有相关性。因此，需要一种能对样本依赖关系建模的方法。
一元势：一个像素自身的能量
二元势：两个相邻像素之间的能量。比如在图像分割中，二元势函数是一个惩罚项，对距离较近、特征相似的像素被设置为不同类标作出较大的惩罚。）
连续条件随机场（CRF）：

所提出的方法可以用于一般场景的深度估计，而无需几何先验或任何额外的信息注入。在我们的情况下，可以解析计算分区函数的积分，因此我们可以精确地解决对数似然优化。此外，由于存在封闭形式的解决方案，解决用于预测新图像深度的MAP问题非常有效。我们通过实验证明，该方法在室内和室外场景数据集上均优于最新的深度估计方法。

最大后验概率（maximum a posteriori，MAP）：来源于贝叶斯统计学，其估计值是后验概率分布（posterior distribution）的众数。最大后验概率估计可以对实验数据中无法直接观察到的量提供一个点估计（point estimate）。它与Fisher的最（极）大似然估计（Maximum Likelihood，ML）方法相近，不同的是MAP通过考虑被估计量的先验概率分布（prior distribution）扩充了优化的目标函数，使得目标函数中融合了预估计量的先验分布信息，因此，最大后验概率估计可以看作是正则化（regularization）的最大似然估计。

Introduction

从描述一般场景的单眼图像中估计深度是计算机视觉中的一个基本问题，在场景理解、三维建模、机器人技术等领域得到了广泛的应用。这是一个众所周知的不适定问题（ill-posed），因为一个捕获的图像可能对应到许多真实世界的场景，[1]。

适定问题是指定解满足下面三个要求的问题：① 解是存在的；② 解是唯一的；③ 解连续依赖于定解条件，即解是稳定的。这三个要求中，只要有一个不满足，则称之为不适定问题（ill-posed）。特别地，如果条件③不满足，那么就称为阿达马意义下的不适定问题。

然而对于人类来说，从单一图像推断潜在的三维结构并不困难，这对于计算机视觉算法来说仍然是一项具有挑战性的任务，因为没有可靠的线索可以利用，如时间信息、立体通信等。

• 先前的工作主要集中在执行几何假设，例如盒子模型，以推断房间[2,3]或室外场景[4]的空间布局。这些模型具有先天性限制，这些限制是仅对特定场景结构建模的限制，因此不适用于一般场景深度估计。
• 后来，探索了非参数方法[5]，该方法包括候选图像检索，场景对齐，然后使用具有平滑性约束的优化进行深度推断。这是基于这样的假设，即具有语义相似外观的场景在密集对齐时应具有相似的深度分布。但是，该方法易于在不同的解耦阶段传播错误，并且严重依赖于构建合理大小的图像数据库来执行候选检索。
• 近年来，已努力整合其他信息源，例如用户注释[6]，语义标签[7,8]。在[8]的最新工作中，Ladicky等人证明联合执行深度估计和语义标记可以互利。但是，所有这些方法都使用手工制作的功能。

与以前的工作不同，我们建议将深度估计公式化为一个深层的连续CRF学习问题，而无需依赖任何几何先验或任何额外信息。条件随机场（CRF）[9]是用于结构化预测的流行图形模型。虽然在分类（离散）域中进行了广泛研究，但对于回归（连续）问题，对CRF的探索较少。关于连续CRF的开创性工作之一可以归因于[10]，在该文献中它被建议用于文档检索的全球排名。在某些约束下，由于可以解析计算分区函数，因此它们可以直接解决最大似然优化。从那时起，连续CRF已用于解决各种结构化回归问题，例如遥感[11,12]，图像去噪[12]。受所有这些成功的启发，鉴于深度值的连续性质，我们在此建议将其用于深度估计，并学习深度卷积神经网络（CNN）中的潜在函数。

近年来，目睹了深度卷积神经网络（CNN）的繁荣。 CNN功能已经为各种视觉应用创造了新的记录[13]。尽管在分类问题上取得了所有成功，但针对结构化学习问题（即深度CNN和图形模型的联合训练）的探索较少，这是一个相对较新且尚未很好解决的问题。据我们所知，还没有成功地将这种模型用于深度估计。我们在这里通过共同探索CNN和连续CRF来弥合这一差距。

综上所述，我们重点介绍这项工作的主要贡献如下：

• 我们通过探索CNN和连续CRF，提出了深度卷积神经场模型用于深度估计。考虑到深度值的连续性质，可以解析计算概率密度函数中的分区函数，因此我们可以直接求解对数似然优化而无需任何近似。可以在反向传播训练中精确计算梯度。而且，由于存在封闭形式的解决方案，解决用于预测新图像深度的MAP问题是非常有效的。
• 我们在统一的深度CNN框架中共同学习CRF的一元势函数和二元势函数，并使用反向传播对其进行了训练。
• 我们证明了所提出的方法在室内和室外场景数据集上都优于深度估计的最新结果。

本篇论文优势：

①我们不采用任何这些启发式方法改进我们的结果，但我们就相对误差而言取得了更好的结果。
②为了克服过拟合，其他方法必须收集数以百万计的带有附加标签的图像训练他们的模型。一个可能的原因是，他们的方法捕捉到绝对像素的位置信息，他们可能需要一个非常大的训练集覆盖所有可能的像素布局。相比之下，我们只使用没有任何额外数据标准的训练集，但我们获得相媲美，甚至更好的性能。
③我们的模型只有一元项的时候，相当于带有模糊边界的粗糙预测。通过加入平滑项，我们的模型产生了更好的可视化，接近ground-truth。

Related Work

先前的工作[7,14,15]通常将深度估计表示为一个马尔可夫随机场(MRF)学习问题。由于精确的MRF学习和推理一般是棘手的，这些方法大多采用近似方法，如多条件学习(MCL)、粒子信念传播(PBP)。预测一个新图像的深度是低效的，在[15]中大约需要4-5秒，在[7]中甚至需要更长的时间（30秒）。更糟糕的是，这些方法缺乏灵活性，因为[14,15]依赖于图像的水平对齐，而[7]需要预先对可用的训练数据进行语义标记。最近，Liu等人[16]提出了一个离散-连续的CRF模型，以考虑相邻超像素之间的关系，例如，遮挡。他们还需要使用近似的方法来学习和地图推理。此外，他们的方法依赖于图像检索来获得合理的初始化。相比之下，我们在这里提出了一个深度连续的CRF模型，其中我们可以直接求解对数似然优化，而不需要任何近似，因为配分函数可以解析计算。由于存在封闭形式的解，预测新图像的深度是高效的。此外，我们的模型没有注入任何几何先验或任何额外的信息。

另一方面，以前的方法[5,7,8,15,16]都在他们的工作中使用了手工制作的特性，如德克斯顿、GIST、SIFT、PHOG、对象库等。相比之下，我们学习深度CNN来构造CRF的一元势和成对势。通过联合探索CNN和连续CRF的能力，我们的方法在室内和室外场景深度估计方面都优于最先进的方法。也许最相关的工作是[1]最近的工作，它与我们在这里的工作同步。他们训练两个cnn从一幅图像中预测深度图。然而，我们的方法与他们的方法有很大的不同。他们使用CNN作为一个黑盒，通过卷积直接回归输入图像的深度图。相比之下，我们使用CRF显式地建模相邻超像素的关系，并在一个统一的CNN框架中学习潜力。[1]中该方法的一个潜在缺点是，它倾向于通过位置偏好来学习深度，这很容易适应特定的布局。这在一定程度上解释了为什么他们必须收集大量的标记数据来覆盖所有可能的布局来训练网络(他们使用d收集额外的训练图像。

在[17]最近的工作中，Tompson等人提出了一种混合架构，用于联合训练深度CNN和MRF用于人体姿态估计的架构。它们首先分别训练一个一元项和一个空间模型，然后将它们作为一个微调步骤联合学习。在对整个模型进行微调的过程中，它们只是简单地去除配分函数。相比之下，我们的模型执行连续变量预测。由于配分函数是可积的，可以解析计算，我们可以直接求解对数似然优化。此外，在预测过程中，我们有了地图推理的封闭解。

Deep convolutional neural fields

Overview

我们假设一幅图像是由小的均匀区域（超像素）组成，图模型是由结点组成，超像素表示图中的结点。
由于框架具有灵活性，因此可以应用在像素和超像素上。

超像素：由一系列位置相邻且颜色、亮度、纹理等特征相似的像素点组成的小区域。基于超像素可以是把一幅像素级（pixel-level）的图，划分成区域级（district-level）的图，是对基本信息元素进行的抽象。这些小区域大多保留了进一步进行图像分割的有效信息，且一般不会破坏图像中物体的边界信息。

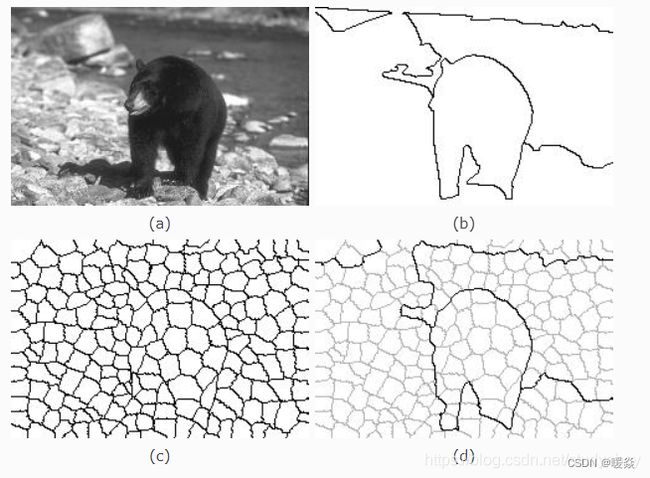
（a）原始图像，（b）基于人类视角的分割图（groundtruth），（c）超像素分割的图像，（d）基于（c）进行分割的图像

超像素—学习笔记 - studyebo - CSDN
超像素(Superpixel)的大致原理以及State-of-the-art？ - 留德华叫兽的回答 - 知乎

每个超像素由它的质心(centroid)的深度所描述。我们使用x表示一幅图像， y = [y1, . . . , yn]T ∈ R_n表示图像x中所有的n个超像素所对应的连续深度值的一个vector。

类似于传统的CRF，我们下边的密度函数来建立数据的条件概率分布模型。

其中，E是势能函数(energy function)；Z是配分函数(partition function)，被定义为：

为了预测一个新图像的深度，we solve the maximum a posteriori(MAP) inference problem:

我们把势能函数看成是在结点**（超像素）N的一元势能U和在图像X边缘的二元势能V**的组合：

其中，一元项U的目的是回归单个超像素的深度值；二元项V鼓励有相似外观的邻近超像素采取相似的深度。我们的目标是在一个统一的CNN框架中，共同学习U和V。

Neural Network Structure

整个网络由一元部分（a unary part），二元部分（a pairwise part）和CRF损失层组成。

首先将一个输入图像，分割（over-segment）成N个超像素，我们考虑图像块（image patches）围绕每个超像素的质心。

The Unary Part

将所有image patches resize为224×224 pixels后作为输入，放到每一个CNN中，输出一个包括n个超像素回归深度值的n维向量。

一元部分的网络由5个卷积层和4全连接层组成。

CNN的参数被所有的超像素共享。注意各层的激活函数问题。

一个image patch输出一个超像素的一维实数值。

The Pairwise Part

把所有邻近超像素对的相似向量（每个包括k个组件）作为输入，把它们放在全连接层（参数被不同的超像素对共享），然后输出一个包含每个相邻超级像素对的所有一维相似性的向量。

The CRF Loss Layer

一元部分和二元部分输出值作为CRF损耗层的输入来最小化负对数似然函数。

这个模型两个潜在的优点是：
1）实现平移不变性，因为我们构建一元势能不考虑超像素的坐标；
2）成对势能由邻近超像素的关系组成

Potential functions

Unary potential

一元势能

这里，z_p是由CNN参数θ参数化的超像素p的回归深度。

Pairwise potential

二元势能

我们从相似观察值的K个类型构造二元势能，它们利用邻近超像素的一致性信息执行平滑：

其中，$R_{pq}$表示一个相邻超像素对(p,q)在the pairwise part的输出，在这里我们使用一个全连接层：

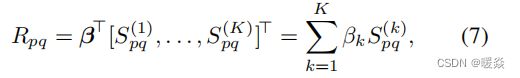
$S^{(k)}$：第k个相似矩阵，它是对称的，其元素是$S_{pq}^{(k)}$
$\beta =[{\beta }_1,{\beta }_2,...,{\beta }_k{]}^T$是神经网络的参数。

To guarantee Z(x)is integrable, we require β_k ≥ 0.

我们通过颜色差异，颜色直方图差异和局部二进制模式（LBP）的纹理差距这三种类型来衡量成对相似性。其卷积形式为：$S_{pq}^{(k)}$=

Learning

由于在公式中的势能函数y的二次项和A的正定性，我们可以解析计算公式(2)这个配分函数的积分：

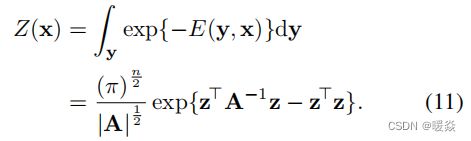
则，根据公式(1),(10),(11),概率分布函数为：

【注】
$x^{(i)},y^{(i)}$指的是第i个训练函数和其对应的深度图。
N是指训练图片的数量。
λ1 and λ2 are weight decay parameters
使用基于后向传播的随机梯度下降(SGD)来进行公式的优化

Implementation details

我们基于高效的CNN工具箱VLFeat MatConvNet1[20]实现了网络的训练。训练是在标准桌面上完成的，使用NVIDIAGTX780GPU，6GB内存。在每次SGD迭代过程中，需要处理大约∼700个超像素的图像块。6GB的GPU可能无法一次处理所有的图像块。因此，我们将一幅图像的超像素图像块划分为两部分，并依次进行处理。在训练整个网络时，使用∼700超像素处理一幅图像大约需要10秒（包括向前和向后）。

在实施过程中，我们使用从 ImageNet中训练的CNN模型，初始化图2中一元部分的前6层。首先，我们不会通过固定前6层来进行反向传播，并使用以下设置来训练网络的其余部分（我们将此过程称为预训练过程）：动量设置为0.9，权值衰减参数λ1，λ2设置为0.0005。在训练前，学习速率初始化为0.0001，每20个周期降低40%。然后我们运行了60个运动周期来报告训练前的结果（学习率下降了两次）。预训练相当有效，在Make3D数据集上训练大约需要1小时，推断新图像的深度需要不到0.1秒。然后，我们用相同的动量和权值衰减来训练整个网络。我们在图2的前两个全连接层中应用比值为0.5的dropout。在Make3D数据集上训练整个网络大约需要16.5个小时，在NYUv2数据集上大约需要33个小时。从头开始预测一个新图像的深度需要∼1.1s。

Experiments

NYU v2: Indoor scene reconstruction

NYUv2数据集由1449张室内场景的RGBD图像组成，其中795张用于训练，654张用于测试（我们使用数据集提供的标准训练/测试分割）。根据[16]，我们在训练前将图像的大小调整为427×561像素。

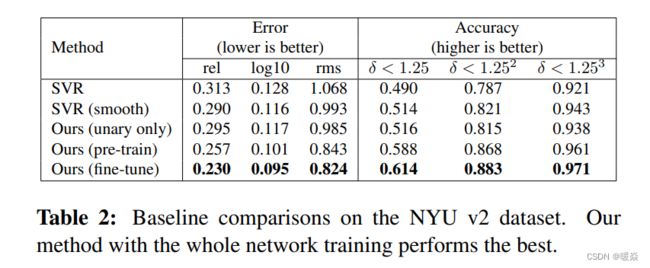
为了对我们的模型进行详细的分析，我们首先基于三种基线方法进行了比较，并在表2中报告了结果。从表中可以得出几个结论：

1)仅用一元项训练时，深层网络有利于更好的性能，这表明我们的一元模型优于SVR模型；
2)在SVR或一元模型中添加平滑项有助于提高预测精度；
3)我们的方法在统一的深度CNN框架中联合学习一元势能和二元势能的参数，取得了最好的性能。

此外，对整个网络进行微调还可以进一步提高性能。这些都很好地证明了我们的模型的有效性。

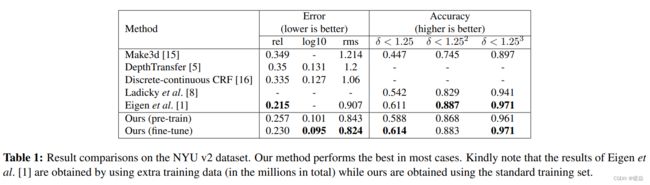
在表1中，我们将我们的模型与几种流行的最先进的方法进行了比较。可以观察到，我们的方法优于经典的方法，如Make3d[15]，深度传输[5]。最值得注意的是，我们的结果明显优于[8]，后者联合利用了深度估计和语义标记。与Eigen等人[1]最近的工作相比，我们的方法通常性能相当。但我们的方法在均方根(rms)误差方面得到了明显更好的结果。请注意，为了克服过度拟合，他们必须收集数百万张额外的标记图像来训练他们的模型。一个可能的原因是，他们的方法捕获了绝对的像素位置信息，他们可能需要一个非常大的训练集来覆盖所有可能的像素布局。相比之下，我们只使用标准的训练集（795），没有任何额外的数据，但我们取得了类似甚至更好的性能。图3显示了我们的方法与Eigen等人的[1]进行了比较的一些定性评价（我们从作者的网站上下载了[1]的预测结果）。与[1]的预测相比，我们的方法产生更视觉愉快的预测，更尖锐的过渡，与局部细节对齐。

Make3D: Outdoor scene reconstruction

Make3D数据集包含534张描绘户外场景的图像。正如[15,16]中指出的，该数据集有局限性：深度的最大值为81米，遥远的物体都映射到81米的一个距离。作为一种补救措施，在[16]中使用了两个标准来报告预测误差：(C1)误差仅在地面真实深度小于70米的区域进行计算；(C2)计算整个图像的误差。我们按照本方案报告评估结果。


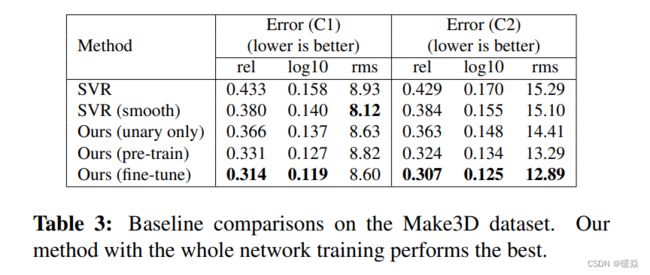
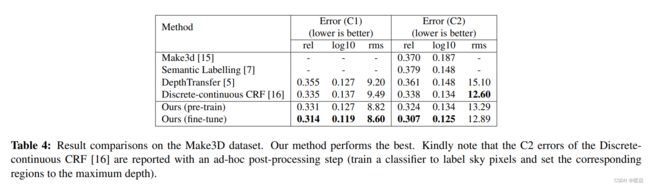
同样地，我们首先在表3中展示了基线比较，从中可以得出与NYUv2数据集类似的结论。然后，我们展示了与表4中几种最先进的方法相比较的详细结果。可以观察到，我们的全网络训练模型的整体性能排名第一，远远优于比较方法。请注意，[16]的C2误差是通过一个特别的后处理步骤来报告的，该步骤训练一个分类器来标记天空像素，并将相应的区域设置为最大深度。相比之下，我们没有使用任何这些启发式方法来重新改善我们的结果，但我们在相对误差方面获得了更好的结果。定性评价的一些例子如图4所示。结果表明，我们的一元模型给出了相当粗糙的预测和模糊的边界。通过添加平滑项，我们的模型产生了更好的可视化，这是接近地面真相。

Appendix

Technical Details（ Deep Convolutional Neural Fields）

Experiments （superpixel number）

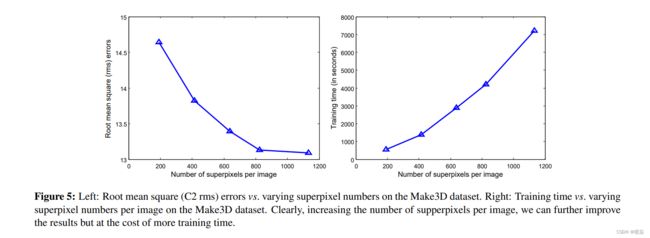
为了展示超像素数如何影响我们的模型的性能，我们添加了一个实验，通过改变每幅图像的超像素数，来评估我们的训练前模型在制作三维数据集上的均方根(rms)误差和训练时间。计算结果如图5所示。正如我们所看到的，增加每幅图像的超像素数会进一步减少均方根误差，但代价是花费更多的训练时间。在本文的所有其他实验中，我们对每张图像使用∼700超像素，因此通过增加它，我们可以期待更好的结果。

References

[1] D. Eigen, C. Puhrsch, and R. Fergus, “Depth map prediction from a single image using a multi-scale deep network,” in Proc. Adv.
Neural Inf. Process. Syst., 2014.
[2] V. Hedau, D. Hoiem, and D. A. Forsyth, “Thinking inside the box: Using appearance models and context based on room geometry,”
in Proc. Eur. Conf. Comp. Vis., 2010.
[3] D. C. Lee, A. Gupta, M. Hebert, and T. Kanade, “Estimating spatial layout of rooms using volumetric reasoning about objects and
surfaces,” in Proc. Adv. Neural Inf. Process. Syst., 2010.
[4] A. Gupta, A. A. Efros, and M. Hebert, “Blocks world revisited: Image understanding using qualitative geometry and mechanics,” in
Proc. Eur. Conf. Comp. Vis., 2010.
[5] K. Karsch, C. Liu, and S. B. Kang, “Depthtransfer: Depth extraction from video using non-parametric sampling,” IEEE Trans.
Pattern Anal. Mach. Intell., 2014.
[6] B. C. Russell and A. Torralba, “Building a database of 3d scenes from user annotations,” in Proc. IEEE Conf. Comp. Vis. Patt.
Recogn., 2009.
[7] B. Liu, S. Gould, and D. Koller, “Single image depth estimation from predicted semantic labels,” in Proc. IEEE Conf. Comp. Vis.
Patt. Recogn., 2010.
[8] L. Ladick, J. Shi, and M. Pollefeys, “Pulling things out of perspective,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2014.
[9] J. D. Lafferty, A. McCallum, and F. C. N. Pereira, “Conditional random fields: Probabilistic models for segmenting and labeling
sequence data,” in Proc. Int. Conf. Mach. Learn., 2001.
[10] T. Qin, T.-Y. Liu, X.-D. Zhang, D.-S. Wang, and H. Li, “Global ranking using continuous conditional random fields,” in Proc. Adv.
Neural Inf. Process. Syst., 2008.
[11] V. Radosavljevic, S. Vucetic, and Z. Obradovic, “Continuous conditional random fields for regression in remote sensing,” in Proc.
Eur. Conf. Artificial Intell., 2010.
[12] K. Ristovski, V. Radosavljevic, S. Vucetic, and Z. Obradovic, “Continuous conditional random fields for efficient regression in large
fully connected graphs,” in Proc. National Conf. Artificial Intell., 2013.
[13] A. Sharif Razavian, H. Azizpour, J. Sullivan, and S. Carlsson, “CNN features off-the-shelf: An astounding baseline for recognition,”
in Workshops IEEE Conf. Comp. Vis. Patt. Recogn., June 2014.
[14] A. Saxena, S. H. Chung, and A. Y. Ng, “Learning depth from single monocular images,” in Proc. Adv. Neural Inf. Process. Syst.,
2005.
[15] A. Saxena, M. Sun, and A. Y. Ng, “Make3D: Learning 3d scene structure from a single still image,” IEEE Trans. Pattern Anal. Mach.
Intell., 2009.
[16] M. Liu, M. Salzmann, and X. He, “Discrete-continuous depth estimation from a single image,” in Proc. IEEE Conf. Comp. Vis. Patt.
Recogn., 2014.
[17] J. Tompson, A. Jain, Y. LeCun, and C. Bregler, “Joint training of a convolutional network and a graphical model for human pose
estimation,” in Proc. Adv. Neural Inf. Process. Syst., 2014.
[18] A. Krizhevsky, I. Sutskever, and G. E. Hinton, “ImageNet classification with deep convolutional neural networks,” in Proc. Adv.
Neural Inf. Process. Syst., 2012.
[19] T. Ojala, M. Pietikainen, and D. Harwood, “Performance evaluation of texture measures with classification based on kullback
discrimination of distributions,” in Proc. Int. Conf. Pattern Recognition, 1994.
[20] A. Vedaldi, “MatConvNet,” http://www.vlfeat.org/matconvnet/, 2013.
[21] K. Chatfield, K. Simonyan, A. Vedaldi, and A. Zisserman, “Return of the devil in the details: Delving deep into convolutional nets,”
in Proc. British Mach. Vision Conf., 2014.
[22] P. K. Nathan Silberman, Derek Hoiem and R. Fergus, “Indoor segmentation and support inference from rgbd images,” in Proc. Eur.
Conf. Comp. Vis., 2012.
[23] R. Achanta, A. Shaji, K. Smith, A. Lucchi, P. Fua, and S. S¨usstrunk, “SLIC superpixels compared to state-of-the-art superpixel
methods,” IEEE Trans. Pattern Anal. Mach. Intell., 2012.