Single-Image Depth Estimation Based on Fourier Domain Analysis论文学习

Jae-Han Lee, Minhyeok Heo, Kyung-Rae Kim, and Chang-Su Kim
Korea University
2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition

摘要

提出了一种基于傅里叶频域分析的单幅图像深度估计的深度学习算法。首先，我们建立了一个卷积神经网络结构，并提出了一个新的损失函数，称为深度平衡欧几里得损失，可以对很大范围的深度进行可靠的训练。然后，我们通过裁剪具有不同裁剪比例的输入图像来生成多个深度图候选。一般来说，小比例的裁剪图像能更可靠地产生深度细节，而大比例的裁剪图像则能更可靠地提供整体深度分布。为了利用这些互补性质，我们将频域中的多个候选项组合起来。实验结果表明，该算法具有较好的性能。通过频域分析，验证了该算法在大多数频段的有效性。

介绍

深度估计是使用一个或多个图像预测场景深度图的过程。深度信息是理解场景中几何关系的重要线索。例如，RGBD图像具有颜色和深度通道，可以应用于各种任务，如三维模型重建[13, 30, 33]，场景识别[27,32,33]，人体姿态估计[37]。深度可以通过立体图像[31]或运动序列[2,7,17,31,40]来估计，深度信息为理解三维结构提供了较为丰富的信息。相比之下，从一张图像估计深度更具有挑战性和模糊性[1,3,5,6,15,19 - 22,24,28,38,42,43],它没有从立体图像或时间帧估计时之间的对应匹配。
为了克服单幅图像深度估计的模糊性，人们对多种几何或图像合成进行了各种假设[9,10,13,23,36,41]。例如,假设场景由平面[13]构成，或图像在特定的角度[9]组成，或场景有地板-墙壁的几何形状[4]，则可以进行三维重建。此外，在[41]中利用了focal blurs，在[9]中使用了从暗通道先验推断的霾强度。然而，只有当相应的假设是有效的时，这些技术才能在特定的情况下重建深度。
近年来，提出了几种基于图的模型[21,23,29,30]，如马尔可夫随机场(Markov random field, MRF)和条件随机场(CRF)。
此外，随着深度学习技术的快速发展[11,12,16]，研究者们进行了各种利用卷积神经网络(convolutional neural networks, CNNs)进行单图像深度估计的尝试[3,5,6,19,38]。
在本文中，我们提出了一种基于cnn的单幅图像深度估计算法，该算法在傅里叶频域内进行了多次预测，并结合了预测结果。首先，我们开发了一个基于ResNet[11]架构的CNN。它包括用于提取中间特征的附加路径。同时，为了在较宽的深度范围内对网络进行可靠的训练，提出了深度均衡算法欧几里德损失函数。然后，我们通过裁剪具有不同裁剪比的输入图像来生成多个深度图候选项。一般来说，小裁剪比的裁剪图像重建局部深度细节更真实，而大裁剪比的裁剪图像更可靠地恢复整体深度分布。为了利用这些互补性质，我们将傅里叶频域中的多个候选项结合起来。
在NYUv2深度数据集[33]上的大量实验结果表明，该算法具有最先进的性能，显著优于传统算法。此外，通过分析频域估计深度图，验证了该算法各分量在较宽频率范围内的有效性。
本文的主要贡献有三:
•我们设计了一个基于resnet的深度估计网络。
•我们提出DBE损失，以使网络的训练更加可靠。
•据我们所知，这是第一个对单图像深度估计问题进行傅里叶分析的研究。并提出了一种精确可靠的频域多深度组合方案。

相关工作

对单幅图像的深度估计进行了各种尝试。例如Saxena等人的[29]采用了多尺度MRF考虑图像的全局上下文以及其局部特征，用于深度估计。
在[30]中，他们将图像分割成均匀的小块，利用MRF获取每个小块的三维参数，重构出三维结构。Kersh等人提出将数据集中参考RGBD图像的深度图转换为输入彩色图像。同样，Liu等人利用参考RGBD图像中的深度信息,他们用它来表示用于深度估计的CRF模型中的一元势。Ladicky等人[18]将深度估计问题表述为预测每个像素处于规范深度的可能性问题，并试图将深度估计与语义分割结合起来解决。

提出的算法

深度预测网络结构

基于ResNet-152


对此网络进行两阶段的训练，在第一阶段，我们在去除附加的特征提取部分，只保留原有的ResNet-152结构对网络进行训练。我们从ResNet-152参数开始，为图像分类任务进行预训练，然后使用训练图像及其地面真值深度图对它们进行微调。在第二阶段，我们从第一阶段的参数开始，但用高斯随机值初始化附加特征提取的参数。该两阶段方法不仅提高了训练速度，而且提高了深度估计性能。

深度平衡欧几里得损失

回归问题中，欧几里得损失经常使用：

令$\omega$为网络参数，其更新如下：

在实践中，绝对估计误差|${\hat{d}}_x-d_x$| 由于实际深度更大，因此趋向于更大。 例如，远物体的3％深度误差大于近物体的3％误差。 因此，（2）中的偏导数受到远距离物体的深度估计误差的影响比对近物体的深度估计误差影响更大。 因此，当采用欧几里德损失时，训练网络来估计远距离的物体的深度比预测近距离物体的深度更可靠。为了克服这个问题，我们提出了一种新的损失，称为深度平衡欧氏（DBE）损失，由下式给出


所以有

我们设$a_1$是一个相对较大的数，$a_2$是一个负数。然后,一般来说,$d_x$更深的深度,更大误差的影响(g(${\hat{d}}_x$)−g ($d_x$))可以减少一个较小的因素($a_1+a_2{\hat{d}}_x$)。因此，该网络可以训练成可靠地估计浅层深度和深层深度。第4节的实验结果也将证实，提出的DBE损失比原欧几里德损失更能有效地进行深度估计。

深度候选图的生成

使用由DBE损失训练的所提出的CNN，我们为输入图像生成多个深度图候选。 图3（a）示出了如何生成深度图候选。 首先，我们分别使用裁剪率r裁剪四个角的输入图像。 裁剪比率被定义为裁剪图像与整个图像的尺寸比率。 其次，我们通过CNN处理每个裁剪的图像以产生相应的深度图。 最后，我们将这四个部分估计的深度图合并为一个深度图候选者。 在合并过程中，请注意所有深度值都应缩放1 / r，以补偿裁剪图像中的对象看起来更近的缩放效果。 在缩放之后，将部分深度图转换为它们的位置然后叠加。对于重叠区域中的叠加，执行平均。让${\hat{D}}_r$表示合成的深度图候选者。当r = 1时，将整个图像通过CNN得到${\hat{D}}^1$。
由于CNN参数不对称，因此翻转图像不会产生翻转深度图。因此，我们水平翻转输入图像，获得具有裁剪率r的深度图候选，并且翻转深度图候选。这表示为${\hat{D}}_{flip}^r$。图3（b）〜（e）示出了深度图候选的示例。

傅里叶域中的候选图结合

如图3所示，通常，具有较大裁剪率r的深度图候选${\hat{D}}_r$更可靠地重建整体深度分布，而具有较小r的深度图候选${\hat{D}}_r$更准确地估计局部细节。 为了利用这些互补属性，我们在傅立叶频域中组合了深度图候选。 注意，整体分布和局部细节分别对应于低频和高频系数。 尺寸为M×N的输入信号I(x，y)的离散傅里叶变换（DFT）[26]由下式给出：

其中u和v是水平和垂直频率(我理解应该是水平分量和竖直分量的意思吧)。
我们将每个深度图候选项进行转换，并将2D-DFT系数重新排列为列向量。在重排过程中，我们消除了两种冗余。首先,DFT是周期性的，即对于所有k, l∈z,有 $F(u,v)=F(u+Nk,v+Ml)$。其次，由于深度映射是实数，它的DFT是共轭对称的，即F(u, v) =$F^{\ast }(-u，-v)$。让${\hat{f}}^m$表示第m个深度图重新排列的列向量。让$\hat{f}$表示所有候选深度图的组合起来的向量，f是ground-truth。${\hat{f}}_k^m,{\hat{f}}_k,f_k$代表${\hat{f}}^m,\hat{f},f$中第K个分量。

M为候选深度图的个数。
首先,偏差$b_k^m$应该弥补${\hat{f}}_k^m$与$f_k$的平均偏差。因此，我们使用训练数据集，定义

其中t为训练图像的索引，T为训练数据集中的图像总数。同时,${\hat{f}}_{kt}^m$和$f_{kt}$分别表示${\hat{f}}_k^m$和$f_k$中的第t个图像。
其次，确定了权重参数$w_k^m$来最小化${\hat{f}}_k$和$f_k$之间的均方误差(MSE)。为此，我们定义了一个矩阵$T_k$，其中第(t, m) 元素等于${\hat{f}}_{k,t}^m-b_k^m$。我们还定义了ground_truth向量$t_k=[f_{k1}，\cdot \cdot \cdot ，f_{kT}{]}^{\prime }$。然后，MSE最小化问题是找到最优权向量$w_k=[w_k^1，\cdot \cdot \cdot ，w_k^M{]}^{\prime }$，由

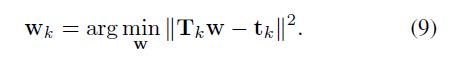
这可以使用$T_k$的伪逆来解决。

奇异矩阵或非方阵的矩阵不存在逆矩阵，但可以用函数pinv(A)求其伪逆矩阵。基本语法为X=pinv(A),X=pinv(A,tol),其中tol为误差：max(size(A))*norm(A)*eps。函数返回一个与A的转置矩阵A’ 同型的矩阵X，并且满足：AXA=A,XAX=X.此时，称矩阵X为矩阵A的伪逆，也称为广义逆矩阵。pinv(A)具有inv(A)的部分特性，但不与inv(A)完全等同。

我们对所有k重复这个过程来确定所有的权重和偏置参数。
在测试中，我们将多个深度图候选者的DFT矢量组合成为最终估计的 $\hat{f}$（7）。 然后，我们执行傅里叶逆变换以生成最终估计的深度图$\hat{D}$,值得指出的是，由于Parseval的关系[26]，最小化频域中的MSE等同于最小化空间域中的MSE。 换句话说，没有其他的${\hat{f}}^m$组合可以在估计和ground-truth深度图之间产生更小的MSE。

摘要

[1] M. Baig and L. Torresani. Coupled depth learning. In Proc.
IEEE WACV, pages 1–10, Mar. 2016.
[2] G. J. Brostow, J. Shotton, J. Fauqueur, and R. Cipolla. Segmentation
and recognition using structure from motion point
clouds. In ECCV, pages 44–57, Oct. 2008.
[3] A. Chakrabarti, J. Shao, and G. Shakhnarovich. Depth from
a single image by harmonizing overcomplete local network
predictions. In NIPS, pages 2658–2666, Dec. 2016.
[4] E. Delage, H. Lee, and A. Y. Ng. A dynamic Bayesian network
model for autonomous 3D reconstruction from a single
indoor image. In Proc. IEEE CVPR, pages 2418–2428, Jun.
2006.
[5] D. Eigen and R. Fergus. Predicting depth, surface normals
and semantic labels with a common multi-scale convolutional
architecture. In Proc. IEEE ICCV, pages 2650–2658,
Dec. 2015.
[6] D. Eigen, C. Puhrsch, and R. Fergus. Depth map prediction
from a single image using a multi-scale deep network. In
NIPS, pages 2366–2374, Dec. 2014.
[7] A. Flint, D. W. Murray, and I. Reid. Manhattan scene understanding
using monocular, stereo, and 3D features. In Proc.
IEEE ICCV, pages 2228–22235, Nov. 2011.
[8] X. Glorot and Y. Bengio. Understanding the difficulty of
training deep feedforward neural networks. In Proc. AISTATS,
pages 249–256, Mar. 2010.
[9] A. Gupta, A. Efros, and M. Hebert. Blocks world revisited:
Image understanding using qualitative geometry and
mechanics. In ECCV, pages 482–496, Sep. 2010.
[10] K. He, J. Sun, and X. Tang. Single image haze removal using
dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell.,
33(12):2341–2353, Dec. 2011.
[11] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning
for image recognition. In Proc. IEEE CVPR, pages 770–778,
Jun. 2016.
[12] K. He, X. Zhang, S. Ren, and J. Sun. Identity mappings
in deep residual networks. In ECCV, pages 630–645, Oct.
2016.
[13] D. Hoiem, A. Efros, and M. Hebert. Automatic photo popup.
ACM Trans. Graph., 24(3):577–584, Jul. 2005.
[14] K. Karsch, C. Liu, and S. B. Kang. Depth extraction from
video using non-parametric sampling. In ECCV, pages 775–
788, Oct. 2012.
[15] K. Karsch, C. Liu, and S. B. Kang. Depth transfer: Depth
extraction from video using non-parametric sampling. IEEE
Trans. Pattern Anal. Mach. Intell., 36(11):2144–2158, Oct.
2014.
[16] A. Krizhevsky, I. Sutskever, and G. E. Hinton. ImageNet
classification with deep convolutional neural networks. In
NIPS, pages 1097–1105, Dec. 2012.
[17] A. Kundu, Y. Li, F. Daellert, F. Li, and J. M. Rehg. Joint semantic
segmentation and 3D reconstruction from monocular
video. In ECCV, pages 703–718, Sep. 2014.
[18] L. Ladicky, J. Shi, and M. Pollefeys. Pulling things out of
perspective. In Proc. IEEE CVPR, pages 89–96, Jun. 2014.
[19] I. Laina, C. Rupprecht, V. Belagiannis, F. Tombari, and
N. Navab. Deeper depth prediction with fully convolutional
residual networks. In Proc. IEEE 3DV, pages 239–248, Oct.
2016.
[20] B. Li, C. Shen, Y. Dai, A. van den Hengel, and M. He. Depth
and surface normal estimation from monocular images using
regression on deep features and hierarchical CRFs. In Proc.
IEEE CVPR, pages 1119–1127, Jun. 2015.
[21] F. Liu, C. Shen, and G. Lin. Deep convolutional neural fields
for depth estimation from a single image. In Proc. IEEE
CVPR, pages 5162–5170, Jun. 2015.
[22] F. Liu, C. Shen, G. Lin, and I. Reid. Learning depth from single
monocular images using deep convolutional neural fields.
IEEE Trans. Pattern Anal. Mach. Intell., 38(10):2024–2039,
Oct. 2016.
[23] F. Liu, C. Shen, G. Lin, and I. Reid. Learning depth from single
monocular images using deep convolutional neural fields.
IEEE Trans. Pattern Anal. Mach. Intell., 38(10):2024–2039,
Oct. 2016.
[24] M. Liu, M. Salzmann, and X. He. Discrete-continuous depth
estimation from a single image. In Proc. IEEE CVPR, pages
716–723, Jun. 2014.
[25] Y. Nesterov. A method of solving a convex programming
problem with convergence rate o(1/k2). Soviet Mathematics
Doklady, 27(2):372–376, Feb. 1983.
[26] A. V. Oppenheim and R. W. Schafer. Discrete-Time Signal
Processing. Prentice Hall, 1989.
[27] X. Ren, L. Bo, and D. Fox. RGB-D scene labeling: Features
and algorithms. In Proc. IEEE CVPR, pages 2759–2766, Jun.
2012.
[28] A. Roy and S. Todorovic. Monocular depth estimation using
neural regression forest. In Proc. IEEE CVPR, pages 5506–
5514, Jun. 2016.
[29] A. Saxena, M. Sun, and A. Y. Ng. 3-D depth reconstruction
from a single still image. Int. J. Comput. Vis., 76(1):53–69,
Oct. 2008.
[30] A. Saxena, M. Sun, and A. Y. Ng. Make3D: Learning 3-D
scene structure from a single still image. IEEE Trans. Pattern
Anal. Mach. Intell., 31(5):824–840, Oct. 2009.
[31] D. Scharstein and R. Szeliski. A taxonomy and evaluation
of dense two-frame stereo correspondence algorithms. Int. J.
Comput. Vis., 47:7–42, Apr. 2002.
[32] J. Shotton, T. Sharp, A. Kipman, A. Fitzgibbon, M. Finocchio,
A. Blake, M. Cook, and R. Moore. Real-time human
pose recognition in parts from single depth images. Commun.
ACM, 56(1):116–124, Jan. 2013.
[33] N. Silberman, D. Hoiem, P. Kohli, and R. Fergus. Indoor
segmentation and support inference from RGBD images. In
ECCV, pages 746–760, Oct. 2012.
[34] K. Simonyan and A. Zisserman. Very deep convolutional
networks for large-scale image recognition. [Online]. Available:
https://arxiv.org/abs/1409.1556.
[35] I. Sutskever, J. Martens, G. Dahl, and G. Hinton. On the
importance of initialization and momentum in deep learning.
In ICML, pages 1139–1147, Feb. 2013.
[36] S. Suwajanakorn and C. Hernandez. Depth from focus with
your mobile phone. In Proc. IEEE CVPR, pages 3497–3506,
Jun. 2015.
[37] J. Taylor, J. Shotton, T. Sharp, and A. Fitzgibbon. The vitruvian
manifold: Inferring dense correspondences for oneshot
human pose estimation. In Proc. IEEE CVPR, pages 103–
110, Jun. 2012.
[38] P. Wang, X. Shen, Z. Lin, S. Cohen, B. Price, and A. L.
Yuille. Towards unified depth and semantic prediction from
a single image. In Proc. IEEE CVPR, pages 2800–2809, Jun.
2015.
[39] D. Xu, E. Ricci, W. Ouyang, X. Wang, and N. Sebe. Multiscale
continuous CRFs as sequential deep networks for
monocular depth estimation. In Proc. IEEE CVPR, pages
5354–5362, Jun. 2017.
[40] K. Yamaguchi, D. McAllester, and R. Urtasun. Efficient joint
segmentation, occlusion labeling, stereo and flow estimation.
In ECCV, pages 756–771, Sep. 2014.
[41] R. Zhang, P.-S. Tsai, J. E. Cryer, and M. Shah. Shape-fromshading:
a survey. IEEE Trans. Pattern Anal. Mach. Intell.,
21(8):690–706, Aug. 1999.
[42] W. Zhuo, M. Salzmann, X. He, and M. Liu. Indoor scene
structure analysis for single image depth estimation. In Proc.
IEEE CVPR, pages 614–622, Jun. 2015.
[43] D. Zoran, P. Isola, D. Krishnan, and W. T. Freeman. Learning
ordinal relationships for mid-level vision. In Proc. IEEE
ICCV, pages 388–396, Dec. 2015.