Pointnet++学习

1、点云的归一化与反归一化
归一化的作用：
数据归一化后，最优解的寻优过程明显会变得平缓，更容易正确的收敛到最优解

def pc_normalize(pc):
    """
    对点云数据进行归一化
    :param pc: 需要归一化的点云数据
    :return: 归一化后的点云数据
    """
    # 求质心，也就是一个平移量，实际上就是求均值
    centroid = np.mean(pc, axis=0)
    pc = pc - centroid
    m = np.max(np.sqrt(np.sum(pc ** 2, axis=1)))
    # 对点云进行缩放
    pc = pc / m
    return pc

def np.mean(a, axis=None, dtype=None, out=None, keepdims=np._NoValue, *,
         where=np._NoValue):
"""
沿指定轴计算算术平均值 
Parameters:
a:需要计算的点云数据
axis:指定轴
	 axis=0:对a数组的每列求平均值
	 axis=1:对a数组的每行求平均值
"""

点云的反归一化：
由于点云的归一化操作，会使得PointNet预测的结果比原始点云尺寸不同，为了恢复原始大小，可以将预测得到的点云进行反归一化，即使得到的点云乘上缩放尺寸m，再加上平移尺寸centroid。

ret = pred × m + centroid

2、os.path.join()函数

os.path.join() 函数用于路径拼接文件路径，可以传入多个参数。

3、Python rstrip()方法
Python rstrip() 删除 string 字符串末尾的指定字符，默认为空白符，包括空格、换行符、回车符、制表符。

4、如何进行sample(采样) ?
PointNet++较PointNet的主要改进是引入了局部特征的思想: 将整个大点云P分成有overlap的小点云，分别利用PointNet对小点云进行特征提取。Sample(采样的目的)就是选出上述小点云的代表点(中心点)，这里实现的方式采用的FPS(fathest point sampling):
a. 有两个集合A = {}, B = P
b. 随机选择B中一个点x加入A, 并从B中删除点x
c. 计算B中每个点z到A中所有点的距离得到z_1, z_2, …, z_len(A), 选择min(z_1, z_2, …, z_len(A)记为点z到集合A的距离;
d. 从B中选择距离集合A最远的点y, 加入到集合A，并从B删除点y.
e. 重复c, d直到集合A中点的数量满足预先设定的阈值.

是不是和图论里的Dijkstra算法很类似，只不过Dijkstra算法求的是最短距离。下面用一张二维图更直观的表示sample的目的: 左图表示输入点，右图表示使用FPS算法采样得到的中心点(红色倒三角形)。这些中心点将用于接下来的group操作。

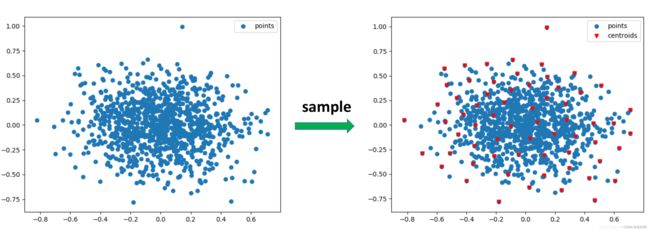
sample的代码(fps算法)的代码如下, 部分是采用的向量化实现，而且在实现的时候有些技巧性；建议首先自己思考一下如何用代码实现上述fps算法:

input和output分别是什么 ? Input: 点集xyz shape=(B, N, 3), 中心点的数量M; Output: M个中心点的坐标或索引centroids, shape=(B, M, 3)或(B, M). 代码中返回的是索引值。

如果不用for循环进行比较距离, 又该如何实现 ? 如果感觉不是很好写，看看下面的代码实现吧。

如何实现点集中的点-点距离的向量化计算 ? 这里实现时遇到了一个坑, 当dist=0时，有可能会出现1e-8之类很小的值，但开根号也没有报错，所以比较好的方式是使用平方距离，或者使用torch.where过滤一下距离等于0的值。

def get_dists(points1, points2):
    '''
    Calculate dists between two group points
    :param cur_point: shape=(B, M, C)
    :param points: shape=(B, N, C)
    :return:
    '''
    B, M, C = points1.shape
    _, N, _ = points2.shape
    dists = torch.sum(torch.pow(points1, 2), dim=-1).view(B, M, 1) + \
            torch.sum(torch.pow(points2, 2), dim=-1).view(B, 1, N)
    dists -= 2 * torch.matmul(points1, points2.permute(0, 2, 1))
    dists = torch.where(dists < 0, torch.ones_like(dists) * 1e-7, dists) # Very Important for dist = 0.
    return torch.sqrt(dists).float()

def fps(xyz, M):
    '''
    Sample M points from points according to farthest point sampling (FPS) algorithm.
    :param xyz: shape=(B, N, 3)
    :return: inds: shape=(B, M)
    '''
    device = xyz.device
    B, N, C = xyz.shape
    centroids = torch.zeros(size=(B, M), dtype=torch.long).to(device)
    dists = torch.ones(B, N).to(device) * 1e5
    inds = torch.randint(0, N, size=(B, ), dtype=torch.long).to(device)
    batchlists = torch.arange(0, B, dtype=torch.long).to(device)
    for i in range(M):
        centroids[:, i] = inds
        cur_point = xyz[batchlists, inds, :] # (B, 3)
        cur_dist = torch.squeeze(get_dists(torch.unsqueeze(cur_point, 1), xyz))
        dists[cur_dist < dists] = cur_dist[cur_dist < dists]
        inds = torch.max(dists, dim=1)[1]
    return centroids

5、如何进行group ?
经过sample操作，我们已经得到了点云P中M个中心点，group的操作就是以每个中心点centroid为圆心，人工设定半径r，每个圆内部的点作为一个局部区域，再利用接下来的PointNet提取特征。这里需要注意的是，为了方便batch操作，每一个局部区域内的点的数量是一致的，都为K，如果某个圆内的点的数量小于K, 则可以重复采样圆内的点，达到数量K；如果某个区域内的点的数量大于K, 则随机选择K个点，即可。group操作得到的结果如下图所示，可以形成很多小的局部区域

Group的代码该怎么写呢? 首先得先考虑清楚一下问题:

group的输入和输出是什么? 输入: 完整点云(B, N, 3), 中心点(B, M), 半径r, 前面提到的数量K; 输出: 很多个局部小点云(B, M, K, 3)或其索引(B, M, K)，下面代码中返回的是索引值, shape为(B, M, K)

难点在于向量化实现选择K个点: 在圆内大于K和小于K时是如何操作的。

具体代码参考如下:

def gather_points(points, inds):
    '''
    :param points: shape=(B, N, C)
    :param inds: shape=(B, M) or shape=(B, M, K)
    :return: sampling points: shape=(B, M, C) or shape=(B, M, K, C)
    '''
    device = points.device
    B, N, C = points.shape
    inds_shape = list(inds.shape)
    inds_shape[1:] = [1] * len(inds_shape[1:])
    repeat_shape = list(inds.shape)
    repeat_shape[0] = 1
    batchlists = torch.arange(0, B, dtype=torch.long).to(device).reshape(inds_shape).repeat(repeat_shape)
    return points[batchlists, inds, :]

def ball_query(xyz, new_xyz, radius, K):
    '''
    :param xyz: shape=(B, N, 3)
    :param new_xyz: shape=(B, M, 3)
    :param radius: int
    :param K: int, an upper limit samples
    :return: shape=(B, M, K)
    '''
    device = xyz.device
    B, N, C = xyz.shape
    M = new_xyz.shape[1]
    grouped_inds = torch.arange(0, N, dtype=torch.long).to(device).view(1, 1, N).repeat(B, M, 1)
    dists = get_dists(new_xyz, xyz)
    grouped_inds[dists > radius] = N
    grouped_inds = torch.sort(grouped_inds, dim=-1)[0][:, :, :K]
    grouped_min_inds = grouped_inds[:, :, 0:1].repeat(1, 1, K)
    grouped_inds[grouped_inds == N] = grouped_min_inds[grouped_inds == N]
    return grouped_inds

6、Pointnet如何提取特征 ?
经过了sample和group操作，整个大点云被分成了很多个有overlap的小点云, 整个完整点云可表示为shape=(B, M, K, C0)的tensor, M表示中心点的数量, K表示每个中心点的球邻域内选择的点的数量, C0是特征维度, 初始输入点位C0=3或C0=6(加上normal信息)。接下来就是利用PointNet对每个小点云P’(shape=(K, C0))进行特征提取。对小点云P’中的每个点连续进行 1d卷积 + bn + relu 操作，学习每个点的特征, 最后在K通道上进行最大值和平均值池化，得到当前小点云的特征F(shape=(C, )), 这里实现时并没有直接用nn.Conv1d，而是使用了nn.Conv2d, kernel size=1, 本质应该是一样的。每个小点云P’(K, C0)经过PointNet得到特征F(C, )， 那么一个batch的数据(shape=(B, M, K, C0)), 经过PointNet模块后, 将会得到维度为(B, M, C)的特征. 这部分代码比较简洁，就是PyTorch的常规操作，部分代码如下:

self.backbone = nn.Sequential()
        for i, out_channels in enumerate(mlp):
            self.backbone.add_module('Conv{}'.format(i),
                                     nn.Conv2d(in_channels, out_channels, 1,
                                               stride=1, padding=0, bias=False))
            if bn:
                self.backbone.add_module('Bn{}'.format(i),
                                         nn.BatchNorm2d(out_channels))
            self.backbone.add_module('Relu{}'.format(i), nn.ReLU())
            in_channels = out_channels

上面就是一次set abstraction操作了. PointNet++是有3次set abstraction操作的:

第一次: (B, N, C0) -> (B, M1, C1) , C0 = 3 或 C0=6(加上normal信息)
第二次: (B, M1, C1+3) -> (B, M2, C2)
第三次: (B, M2, C2+3) -> (B, C3)
这里有一个细节问题, 可以看到C1和C2后面都加了3, 这是在学到特征的基础上又加了位置信息(x, y, z), 重新作为新的特征来送入PointNet网络。

7、分类任务在提取特征后是怎么操作的，loss是什么?
在提取了每个点云的特征(C3, )之后, 接下来就和图像里的分类任务一样了，C3维的特征作为输入，然后通过通过两个全连接层和一个分类层(分类层的是输出节点等于类别数的全连接层),输出每一类的概率。
损失函数采用的是交叉熵损失函数，对应PyTorch中的nn.CrossEntropy().

8、分割任务中如何进行上采样, loss是什么?
分割任务需要对点云P中的每个点进行分类，而PointNet++中的set abstraction由于sampling操作减少了输入点云P中的点的数量，如何进行上采样使点云数量恢复输入时的点云数量呢?
在图像分割任务中，为了恢复图像的分辨率, 往往采用反卷积或者插值的方式来操作呢, 在点云中该如何恢复点云的数量呢?
其实，在PointNet++中的set abstraction模块里，当前点云Q和下采样后的点云Q’的中的点位置信息一直是保存的，点云的上采样就是利用了这一特性。这里利用二维图直观的解释一下，下方左图中红色的倒三角形表示下采样后的点云Q’, 蓝色的点云表示下采样之前的点云Q, 点云里的上采样就是用PointNet学习后的点云Q’的特征表示下采样之前点云Q的特征。采用的方式是k近邻算法，论文中k=3。如图所示，对于Q中的每一个点O，在Q’中寻找其最近的k个点，基于距离加权(距离O近，其权重大; 距离O远, 其权重大)求和这k个点的特征来表示点O的特征，具体计算方式为:

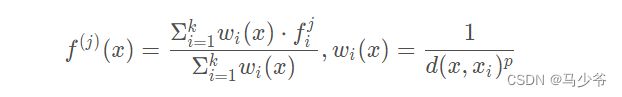
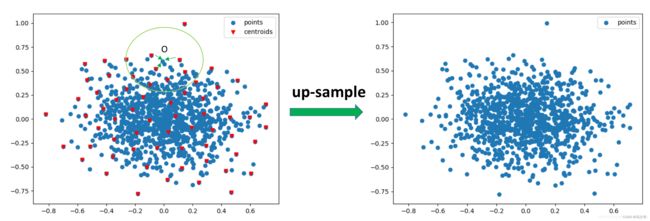
上采样得到了C’维的特征, 而且点的数量已经恢复到了下采样之前的数量; 将C’维的特征与set abstraction中相同点数量的点云(对称位置)特征(C维)进行进行concat操作，进而进行多个 Conv1d + Bn + ReLU操作，来得到新的特征。
经过三次上采样操作后，点云恢复了初始输入点云中点的数量, 再经过一次conv1d + bn + relu层 和一个对点的分类层，最终得到对每个点的分类。

上采样部分的PyTorch实现代码如下:

def three_nn(xyz1, xyz2):
    '''

    :param xyz1: shape=(B, N1, 3)
    :param xyz2: shape=(B, N2, 3)
    :return: dists: shape=(B, N1, 3), inds: shape=(B, N1, 3)
    '''
    dists = get_dists(xyz1, xyz2)
    dists, inds = torch.sort(dists, dim=-1)
    dists, inds = dists[:, :, :3], inds[:, :, :3]
    return dists, inds


def three_interpolate(xyz1, xyz2, points2):
    '''

    :param xyz1: shape=(B, N1, 3)
    :param xyz2: shape=(B, N2, 3)
    :param points2: shape=(B, N2, C2)
    :return: interpolated_points: shape=(B, N1, C2)
    '''
    _, _, C2 = points2.shape
    dists, inds = three_nn(xyz1, xyz2)
    inversed_dists = 1.0 / (dists + 1e-8)
    weight = inversed_dists / torch.sum(inversed_dists, dim=-1, keepdim=True) # shape=(B, N1, 3)
    weight = torch.unsqueeze(weight, -1).repeat(1, 1, 1, C2)
    interpolated_points = gather_points(points2, inds)  # shape=(B, N1, 3, C2)
    interpolated_points = torch.sum(weight * interpolated_points, dim=2)
    return interpolated_points

9、以tensor解析PointNet++网络中维度和尺寸是怎么变化的 ?
骨干网络:
Input data(B, N, 6) -> Set Abstraction[sample(B, 512, 3) -> group(B, 512, 32, 6) -> PointNet(B, 512, 32, 128) -> Pooling(B, 512, 128)] -> Set Abstraction[sample(B, 128, 3) -> group(B, 128, 64, 128 + 3) -> PointNet(B, 128, 64, 256) -> Pooling(B, 128, 256) ] -> Set Abstraction[sample(B, 1, 3) -> group(B, 1, 128, 256 + 3) -> PointNet(B, 1, 128, 1024) -> Pooling(B, 1, 1024)] -> Features(B, 1, 1024)

分类模块:
Features(B, 1024) -> FC(B, 512) -> FC(B, 256) -> Output(B, n_clsclasses)

分割模块:
Features(B, 1, 1024) -> FP[unsapmling(B, 128, 1024) -> concat(B, 128, 1024+256)->PointNet(B, 128, 256)]
-> FP(unsampling(B, 512, 256) -> concat(B, 512, 256+128) -> PointNet(B, 512, 128))
-> FP(unsampling(B, N, 128) -> concat(B, N, 128+6)->PointNet(B, N, 128))
-> Conv1d(B, N, 128) -> Conv1d(B, N, n_segclasses)
上述模块如果能够了解清楚并能写出代码的话，基于PyTorch的PointNet++网络就可以实现了。

10、PointNet++ 的MSG, MRG架构 ?
上述文章主要介绍了PointNet++的SSG(single scale grouping), 为了解决点云中密度分布不均匀的问题，作者提出了MSG(multi-scale grouping)和MRG(multi resolution grouping). 下面这张图是作者论文里的图(在ModelNet40数据集上的实验), 测试了PointNet, SSG, MSG, MRG的性能，横坐标表示的是在预测时点云中点的数量，纵坐标表示的是准确率。从图中可以看到, 在点的数量较多时，SSG, MRG, MSG性能相近，明显高于PointNet; 但随着点云中的点的数量下降，准确率明显下滑的有两条线，有轻微下降趋势的有四条线。明显下滑的两条线是没有采取DP策略的。 即使是PointNet网络在采取了DP策略后，其性能在点的数量小于600也会明显高于SSG.。由此可见，DP在解决点云密度不均匀时发挥了重要作用, 而MSG, MRG貌似显得没那么重要 ? 这里就简单介绍一下MSG的思想。

MSG是指在每次Set Abstraction的时候, 在对某个中心点centroid进行group操作的时候采用不同尺寸(例如0.1, 0.2, 0.4, SSG只有0.2)的半径, 来得到不同大小的局部区域，分别送到不同的PointNet网络中，最终把这些学习到的不同尺度的特征进行concat操作来代表当前中心点centroid的操作。

点云如何数据增强 ?
点云不同于图像，图像中有随机裁剪、缩放、颜色抖动等数据增强方式。在点云里，应该如何做数据增强呢?
点云的数据增强主要包括: 随机旋转，随机平移，随机抖动等, 具体实现代码参考:

DP有什么用，是怎么实现的 ?
DP指的是在训练时随机丢弃一些输入点(DP means random input dropout during training)，这样的训练方式对于预测低密度点云较为有效(相对于输入点云), 即在高密度点云中训练的模型，在低密度点云中进行预测，可以达到和训练集中旗鼓相当的效果。具体来说，人工设置超参数p(论文中p=0.95), 从[0, p]中随机出一个值dr(drouout ratio), 对于点云中的每一个点，随机产生一个0-1的值, 如果该值小于等于dr则表示该点被丢弃。这里有一个细节，某些点被丢弃之后，每个batch中的点的数量就不相同了，为了解决这个问题，所有被丢掉的点使用第一个点代替，这样就维持了每个batch中点的数量相同。具体实现代码如下(代码中的p=0.875):

def random_point_dropout(pc, max_dropout_ratio=0.875):
    dropout_ratio =  np.random.random()*max_dropout_ratio # 0~0.875
    drop_idx = np.where(np.random.random((pc.shape[0]))<=dropout_ratio)[0]
    if len(drop_idx)>0:
        pc[drop_idx,:] = pc[0,:] # set to the first point
    return pc

参考链接：https://blog.csdn.net/zhulf0804/article/details/108530499