简单的聚类算法——KMeans代码

简单来讲，聚类就是在还没有类别的情况下，将物体经过算法自动归为不同的类。而分类是已知类别的情况下，将物体分到不同的类中。这个类别就是标签，所以聚类也可以视作无监督分类算法，这个监督就是指有没有提前认为分好类别。

概述

KMeans算法也叫K均值算法，是最常用的聚类算法，主要思想是：在给定K值和随机初始K个中心点的情况下，把每个点(假设是二维数据)分到离其最近的类簇中心点所代表的类簇中，所有点分配完毕之后，根据一个类簇内的所有点重新计算该类簇的中心点(取平均值)，然后再迭代的进行分配点和更新类簇中心点的步骤，直至类簇中心点的变化很小，或者达到指定的迭代次数，分类停止。

以二维空间为例

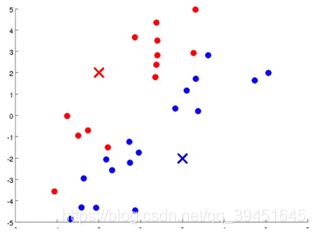
首先随机取两个点作为基准点（叉点），然后逐一计算每个点到这两个基准点的欧式距离（也可以有其他距离、比如余弦距离等），距离哪个基准点近，就将该点归到哪个类中。至此第一次迭代结束。

之后，分别从两部分所有点的坐标中取出平均值的坐标点，再次逐一计算所有点与这两个坐标点的欧式距离，距离哪个坐标距离小，就归到哪个类中。这时会有很多点改变所属类。至此第二次迭代更新结束。

之后不断重复该迭代更新过程，不断更新平均值的坐标点，不断更新所有点的所属类，直到所有点的类别不再改变，算法结束。

上代码

test.py文件

from numpy import *
import kmeans  #文件名
from sklearn.datasets.samples_generator import make_blobs

#数据是聚类样本生成器随机生成的4簇二维点，共1000个
dataSet, _ = make_blobs(n_samples=1000,
                        n_features=2,
                        centers=4,
                        )
dataSet = mat(dataSet)	#转换成矩阵方便操作
k = 4
#调用kmeans文件中的kmeans方法
centroids, clusterAssment = kmeans.kmeans(dataSet, k) 

文件名kmeans.py

from numpy import *
import matplotlib.pyplot as plt


 # 求这两个矩阵的距离
def euclDistance(vector1, vector2):
    return sqrt(sum(power(vector2 - vector1, 2)))  #求得欧氏距离


# 在样本集中随机选取k个样本点作为初始质心
def initCentroids(dataSet, k):
    numSamples, dim = dataSet.shape  # 获取矩阵的行数、列数。行数即为样本数量
    centroids = zeros((k, dim)) #生成一个大小为k*2的零矩阵
    for i in range(k):	#随机取点
        index = int(random.uniform(0, numSamples))
        centroids[i, :] = dataSet[index, :]
    return centroids



# dataSet为一个矩阵。由于数据是n个平面上的点，因此可以看做是n*2的矩阵
# k为将dataSet矩阵中的样本分成k个类
def kmeans(dataSet, k):
    numSamples = dataSet.shape[0]	#获取样本点数量
    clusterAssment = mat(zeros((numSamples, 2)))  # 得到一个N*2的零矩阵，记录点的聚类结果
    clusterChanged = True #标记，如果每个点的所属类别不再变动，那么聚类已稳定
    centroids = initCentroids(dataSet, k)  # 在样本集中随机选取k个样本点作为初始质心

    while clusterChanged:
        clusterChanged = False
        # 遍历每个样本点 
        for i in range(numSamples):
            minDist = 100000.0
            minIndex = 0

            # 计算每个样本点与质点之间的距离，将其归内到距离最小的那一簇
            for j in range(k):
                distance = euclDistance(centroids[j, :], dataSet[i, :])
                if distance < minDist:	# 样本点与4个质心逐一比较，记录最小距离和坐标
                    minDist = distance
                    minIndex = j

			
            # k个簇里面与第i个样本距离最小的簇标号和距离保存在clusterAssment中
            # 若所有的样本不在变化，则退出while循环
            if clusterAssment[i, 0] != minIndex:
                clusterChanged = True
                clusterAssment[i, :] = minIndex, minDist ** 2  # 两个**表示的是minDist的平方

		# 更新每个类别的质心，质心为每个类中所有坐标的平均值
        for j in range(k):
         	# 这句意思不明白的可以看文末链接
            pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]
            # axis=0意思是矩阵列方向上求平均值，返回一个1*n的矩阵
            centroids[j, :] = mean(pointsInCluster, axis=0)

    return centroids, clusterAssment

#画出图像
def showCluster(dataSet , k, centroids, clusterAssment):
    numSamples, dim = dataSet.shape

    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr']
    if k > len(mark):
        print("Sorry! Your k is too large! please contact wojiushimogui")
        return 1

        # draw all samples
    for i in range(numSamples):
        markIndex = int(clusterAssment[i, 0])  # 为样本指定颜色
        plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])

    mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ', 'pb']
    # draw the centroids
    for i in range(k):
        plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=12)

    plt.show()
    

运行结果

参考

https://blog.csdn.net/xinjieyuan/article/details/81477120