空间域图像增强

空间域图像增强

空间域图像增强是指在空间域中，通过线性或非线性变换来增强构成图像的像素。增强的方法主要分为点处理和模板处理两大类。点处理是作用于单个像素的空间域处理方法，包括图像灰度变换、直方图处理、伪彩色处理等技术；而模板处理主要是作用于像素邻域的处理方法，包括图像平滑、图像锐化等技术。

1. 基于灰度变换的图像增强

直接灰度变换属于点处理技术。点处理可将输入图像f(x,y)中的灰度r，通过映射函数T()映射为输出图像g(x,y)中的灰度s。

1.1 灰度线性变换

灰度线性变换表示对输入图像灰度做线性扩张或压缩，映射函数为一个直线方程：
$$g(x,y)=af(x,y)+b$$
其中，a为变换直线的斜率，b为截距
$$\begin{gathered} b=0，且\{\begin{array}{l}a>1对比度扩张\\ a<1对比度压缩\\ a=1相当于复制\end{array} \\ 若b!=0,灰度偏置 \end{gathered}$$
对曝光不足或过度的图像采用灰度线性变换，可以有效改善图像视觉效果。相关代码之前已经学习过。

1.2 分段线性变换（增强对比度）

分段线性变换与灰度线性变换相类似，只不过是对不同灰度范围进行不同的映射处理。

分段线性变换可用于突出受关注目标所在的灰度空间，相对抑制那些不受关注的灰度区间。

1.3 反转变换

反转变换适用于增强嵌入图像暗色区域的白色或灰色细节，特别是当黑色面积占主导地位时。

1.4 对数变换

图像的对数变换将扩展数值较小的灰度范围，压缩数值较大的图像灰度范围。可以用于扩展被压缩的高值图像中的暗像素，其映射函数：$s=clog(1+r)$ 。

1.5 幂次变换

幂次变换是通过幂次曲线中的γ值把输入的窄带值映射到宽带输出值。当γ<1时，把输入的窄带暗值映射到宽带输出亮值；当γ>1时，把输入高值映射为宽带。

1.6 灰度切分

灰度切分是指增强图像中的某一灰度段，其他灰度细节被去掉或者保持不变，其目的在于将某个灰度值范围变得比较突出，用于提取图像中的特定细节。

2. 基于直方图处理的图像增强

2.1 定义

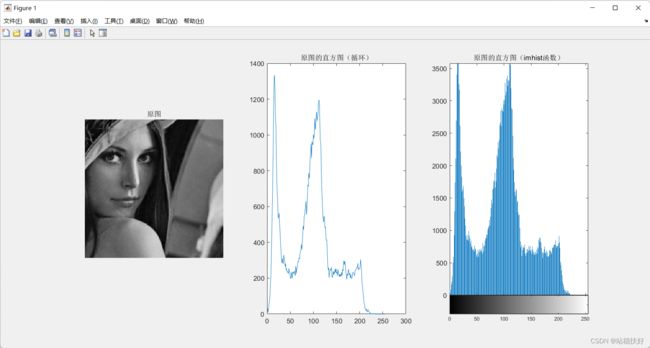
灰度级直方图是图像的一种统计表达，它反映了该图中不同灰度级出现的统计概率，即将图像中不同灰度级的像素进行归一化。

matlab代码如下：

%% 制作图像对应的直方图
I=imread("Images\lena.bmp");
h=zeros(1,256);
[M,N,C]=size(I);
for i=1:M
    for j=1:N 
        k=I(i,j);
        h(k+1)=h(k+1)+1;
    end
end
check_h=imhist(I);
subplot(131);imshow(I);title("原图");
subplot(132);plot(h);title("原图的直方图（循环）");
subplot(133);imhist(I);title("原图的直方图（imhist函数）");

结果如下：

2.2 直方图均衡化

图像直方图描述图像中各灰度级出现的相对频率，基于直方图的灰度变换，可调整图像直方图到一个预定的形状。例如当某一图像由于其灰度值分布集中在较窄的区间，对比度很弱的情况，这时图像细节看不清楚，可采用图像灰度直方图均衡化处理，使得图像的灰度分布趋向均匀，图像所占的像素灰度间距拉开，进而加大图像反差，改善视觉效果，达到增强的目的。

直方图的均衡化处理实际上就是寻找一个灰度变换函数T，使得变换后的灰度值满足s=T®。

以连续数字图像为例，直方图均衡化的灰度变换函数为：
$$s=T(r)={\int }_0^r{p}_r(r)dr$$
对于数字图像的离散情况，则其变换函数与连续时同理，但对原始直方图的积分处理改为累加求和即可。

matlab代码如下：

%% 直方图的均衡化
clc;clear;close all;    % 初始化
I=imread("Images\lena.bmp");I=rgb2gray(I);
k=16;H=histeq(I,k);
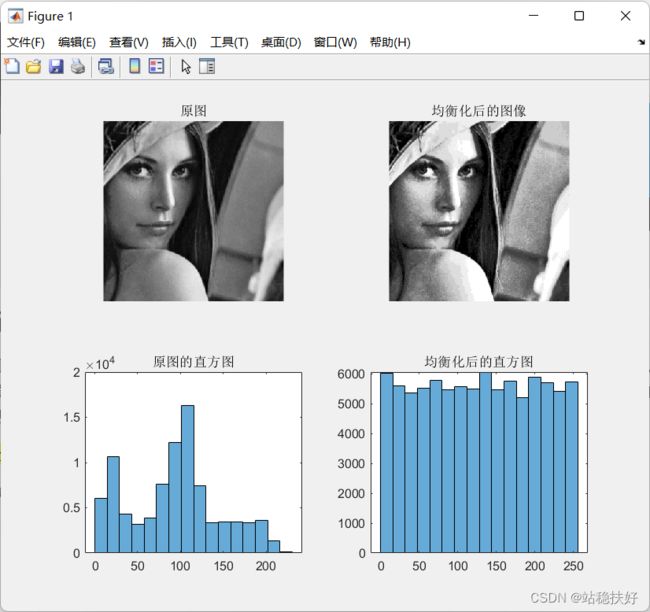
subplot(221),imshow(I,[]),title("原图");
subplot(222),imshow(H,[]),title("均衡化后的图像"),hold on;
subplot(223),histogram(double(I),16),title("原图的直方图");
subplot(224),histogram(double(H),16),title("均衡化后的直方图");

实验结果如下：

由实验结果可知：

1. 变换后直方图趋向平坦，灰级减少，灰度合并。
2. 原始图像含有像素数多的几个灰度级间隔被拉开了，压缩的只是像素数减少的几个灰度级，实际视觉能够接受的信息量大大地增强了。

2.3 直方图规定化

将输入图像灰度分布变换成一个期望的灰度分布直方图，p_r ®为原图的灰度密度函数，p_r (z)是希望得到的灰度密度函数。则s=T( r),v=G(z)（直方图均衡化变换函数），此时图像规定化的逆变换函数为：z=G^-1 (s)=G^-1 (T(r ))，故此时可得，s_k 到z_k 的映射转换。

3. 空间域滤波增强

3.1 基本概念

空间域滤波增强采用模板处理的方法对图像进行滤波，以去除图像噪声或增强图像的细节。空间域滤波增强时，模板的中心从一个像素向另一个像素移动，通过模板运算得到该点的输出。最常用的模板是一个小的3*3二维阵列，模板的系数值决定了处理的性质，如图像平滑或锐化。

3.2 空间域平滑滤波器

任何一副原始图像，在其获取和传输等过程中，会受到各种噪声的干扰，使图像恶化，质量下降，图像模糊，特征淹没，对图像分析不利。

为了抑制噪声、改善图像质量所进行的处理称为图像平滑或去噪，它可以在空间域或频率域中进行。

3.2.1 局部平滑法

局部平滑法是一种直接在空间域上进行平滑处理的方法。假设图像是由许多灰度恒定的小块组成，相邻像素间存在很高的空间相关性，而噪声是统计独立的。因此，可用邻域内各像素的灰度平均值代替该像素原来的值，实现图像的平滑。

定理：设图像中的噪声是随机不相关的加性噪声，窗口内各点噪声是独立同分布的，经过上述平滑后，信号与噪声的方差比可望提高N倍。

例：对图像加入椒盐噪声，采用局部5*5模板进行平滑处理。

matlab代码如下：

%% 图像平滑 使用局部平滑法
close,clc,clear;    %初始化
img=rgb2gray(imread('D:\xcz\matlab_example\Images\lena.bmp'));
subplot(131),imshow(img),title("原图");
img_noise=double(imnoise(img,'salt & pepper',0.06));    %加入椒盐噪声
subplot(132),imshow(img_noise,[]),title("加入椒盐噪声后");
% 局部平滑法，5*5模板处理
img_smoothed=imfilter(img_noise,fspecial('average',5));
subplot(133),imshow(img_smoothed,[]),title("5*5邻域平滑处理");

程序运行结果如下：

采用局部平滑法处理算法简单，但是在降低噪声的同时也会使图像变得模糊了，特别在图像的边缘和细节处。而且领域越大，在去噪能力增强的同时模糊程度会越严重。

3.2.2 超限像素平滑法

对邻域平均法稍加改进，即是超限像素平滑法。它是将f(x,y)和邻域平均g(x,y)差的绝对值与选定的阈值进行比较，根据比较结果决定点(x,y)的最后灰度g(x,y)。其表达式为：
$$g^{\prime }(x,y)=\{\begin{array}{l}g(x,y)|f(x,y)-g(x,y)|>T\\ f(x,y)|f(x,y)-g(x,y)|\le T\end{array}$$
这种算法对抑制椒盐噪声比较有效，对保护仅有微小灰度差的细节及纹理也有效，随着邻域增大，去噪能力增强，但模糊程度也大。同局部平滑法相比，超限像素平滑法的去椒盐噪声效果更好。

3.2.3 灰度最相近的K个邻点平均法

该算法的出发点是：在n*n的窗口内，属于同一集合体的像素，它们的灰度值将高度相关。因此，可用窗口内与中心像素的灰度最接近的K个邻点像素的平均灰度来代替窗口中心像素的灰度值。

较小的K值使噪声方差下降较小，但保持细节效果较好；而较大的K值平滑噪声较好，但会使图像边缘模糊。

实验证明，对于3*3的窗口，取K=6为宜。

3.2.4 空间低通滤波法

领域平均法可以看作一个掩模作用与图像的低通空间滤波，掩模就是一个滤波器，滤波输出的数字图像可以用离散卷积表示为：
$$g(x,y)=\frac{1}{N}\sum _{i=-M}^M\sum _{j=-M}^{M}f(x+i,y+j)h(i,j)$$
常见的掩模有：
$$\frac{1}{9}\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]，\frac{1}{10}\left[\begin{array}{ccc}1& 1& 1\\ 1& 2& 1\\ 1& 1& 1\end{array}\right]，\frac{1}{16}\left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right]，\frac{1}{8}\left[\begin{array}{ccc}1& 1& 1\\ 1& 0& 1\\ 1& 1& 1\end{array}\right]，\frac{1}{2}\left[\begin{array}{ccc}0& \frac{1}{4}& 0\\ \frac{1}{4}& 1& \frac{1}{4}\\ 0& \frac{1}{4}& 0\end{array}\right]$$
掩模不同，中心点或邻域的重要程度都不同，因此，应根据问题的需要选取合适的掩模。但不管什么样的掩模，必须保证全部权系数适合为单位值，这样保证输出图像灰度值在许可范围内，不会发生”溢出“现象。

定理：图像平滑滤波$g(x,y)=\frac{1}{N}{\sum }_{i=-M}^M{\sum }_{j=-M}^{M}f(x+i,y+j)h(i,j)$ 实际上相当于对f(x,y)进行低通滤波，即h(x,y)为低通滤波器。

4. 空间域锐化滤波器

在图像的识别中常常需要突出边缘和轮廓信息，图像锐化就是增强图像的边缘或轮廓。图像平滑通过积分过程使得图像边缘模糊，图像锐化则通过微分使得图像边缘突出、清晰。

4.1 梯度锐化法

图像锐化最常用的方法使梯度法。对于图像f(x,y)，在(x,y)处的梯度定义为：
$$grad(x,y)=\left(\genfrac{}{}{0ex}{}{f_x^{\prime }}{f_y^{\prime }}\right)=\left(\genfrac{}{}{0ex}{}{\frac{\partial f(x,y)}{\partial x}}{\frac{\partial f(x,y)}{\partial y}}\right)$$
梯度是一个矢量，其大小和方向为：
$$\begin{gathered} grad(x,y)=\sqrt{{f_x^{\prime }}^2+{f_y^{\prime }}^2}=\sqrt{(\frac{\partial f(x,y)}{\partial x}{)}^2+(\frac{\partial f(x,y)}{\partial y}{)}^2} \\ \theta =\arctan (\frac{\partial f(x,y)}{\partial y})/(\frac{\partial f(x,y)}{\partial x}) \end{gathered}$$
对于离散图像而言，常用到梯度的大小，因此把梯度大小习惯称为“梯度”。并且一阶偏导数采用一阶差分近似表示，即：
$$f_x^{\prime }=f(x+1,y)-f(x,y)，f_y^{\prime }=f(x,y+1)-f(x,y)$$
同样，为了简化梯度的计算，经常使用：
$$grad(x,y)=max(|f_x^{\prime }|,|f_y^{\prime }|)或grad(x,y)=|f_x^{\prime }|+|f_y^{\prime }|$$
除了梯度算子以外，还可采用Roberts、Prewitt 和 Sobel算子计算梯度，来增强图像边缘。Roberts算子对应的差分计算式为：
$$\begin{gathered} f_x^{\prime }=|f(x+1,y+1)-f(x,y)| \\ {f}_y^{\prime }=|f(x+1,y)-f(x,y+1)| \end{gathered}$$
在锐化图像边缘的同时减少噪声的影响，Prewitt从加大边缘增强算子的模板大小出发，由Roberts的2*2 模板扩大到3*3模板来计算差分，而Sobel算子在Prewitt算子的基础上，对4-邻域采用带权的方法计算差分，如下分别是Roberts、Prewitt 和 Sobel算子的模板：
$$\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)\left(\begin{array}{ccc}-1& 0& 1\\ -1& 0& 1\\ -1& 0& 1\end{array}\right)\left(\begin{array}{ccc}-1& -1& -1\\ 0& 0& 0\\ 1& 1& 1\end{array}\right)\left(\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right)\left(\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ 1& 2& 1\end{array}\right)$$