目标检测 YOLO 系列: 开宗立派 YOLO v1
目标检测 YOLO 系列: 开宗立派 YOLO v1
- 目标检测 YOLO 系列: 开篇
- 目标检测 YOLO 系列: 开宗立派 YOLO v1
- 目标检测 YOLO 系列: 更快更准 YOLO v2
- 目标检测 YOLO 系列: 持续改进 YOLO v3
- 目标检测 YOLO 系列: 你有我有 YOLO v4
- 目标检测 YOLO 系列: 快速迭代 YOLO v5
- 目标检测 YOLO 系列:你有我无 YOLOX
作者:Joseph Redmon,Santosh Divvala , Ross Girshick , Ali Farhadi
发表时间:2015
Paper 原文:You Only Look Once:Unified, Real-Time Object Detection
1 网络结构
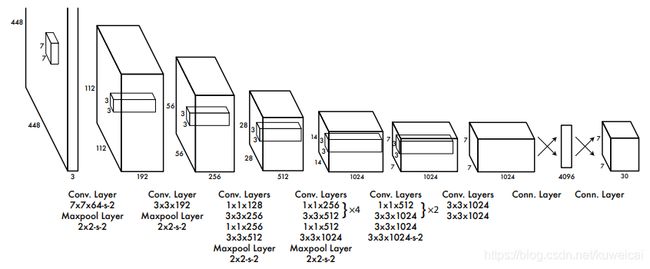
先来看看 YOLO V1 的网络结构,如下图(来自目标检测 YOLO)所示。这里 backbone 是基于 GoogleNet 修改的。
具体来说,这里的 GoogLeNet modification(20 layers)就是采用 1×1 卷积层加 3×3 卷积层替换了 GoogLeNet 中的 Inception 模块,然后去掉了第二层 1x1 的卷积层和最后的 fc 层,更多关于 GoogLeNet 的介绍可以参考 CV 经典主干网络 (Backbone) 系列: GoogLeNet V1 到 V4。
YOLO v1 的具体结构如下。整个网络有 24 个卷积层,2 个全连接层, 4 个 pooling 层,整个网络 的 stride 为 64。
另外除了最后一层使用线性激活函数之外,其他层都使用 Leaky ReLU 激活函数,关于激活函数可以参考深度神经网络中常用的激活函数的优缺点分析。
| index | kernal size | feature map size |
|---|---|---|
| input | - | 3x448x448 |
| conv1 | 64x3x7x7-S_2-P_3 | 64x224x224 |
| pool1 | 2x2-S_2 | 64x112x112 |
| conv2 | 192x3x3-S_1-P_1 | 192x112x112 |
| pool2 | 2x2-S_2 | 192x56x56 |
| conv3 | 128x1x1-S_1-P_0 | 128x56x56 |
| conv4 | 256x3x3-S_1-P_1 | 256x56x56 |
| conv5 | 256x1x1-S_1-P_0 | 256x56x56 |
| conv6 | 512x3x3-S_1-P_1 | 512x56x56 |
| pool3 | 2x2-S_2 | 512x28x28 |
| conv7 | 256x1x1-S_1-P_0 | 256x28x28 |
| conv8 | 512x3x3-S_1-P_1 | 512x28x28 |
| conv9 | 256x1x1-S_1-P_0 | 256x28x28 |
| conv10 | 512x3x3-S_1-P_1 | 512x28x28 |
| conv11 | 256x1x1-S_1-P_0 | 256x28x28 |
| conv12 | 512x3x3-S_1-P_1 | 512x28x28 |
| conv13 | 256x1x1-S_1-P_0 | 256x28x28 |
| conv14 | 512x3x3-S_1-P_1 | 512x28x28 |
| conv15 | 512x1x1-S_1-P_0 | 512x28x28 |
| conv16 | 1024x3x3-S_1-P_1 | 1024x28x28 |
| pool4 | 2x2-S_2 | 1024x14x14 |
| conv17 | 512x1x1-S_1-P_0 | 512x14x14 |
| conv18 | 1024x3x3-S_1-P_1 | 1024x14x14 |
| conv19 | 512x1x1-S_1-P_0 | 512x14x14 |
| conv20 | 1024x3x3-S_1-P_1 | 1024x14x14 |
| conv21 | 1024x3x3-S_1-P_1 | 1024x28x28 |
| conv22 | 1024x3x3-S_2-P_1 | 1024x7x7 |
| conv23 | 1024x3x3-S_1-P_1 | 1024x7x7 |
| conv24 | 1024x3x3-S_1-P_1 | 1024x7x7 |
| fc1 | - | 4096x1 |
| fc2 | - | 1470x1 |
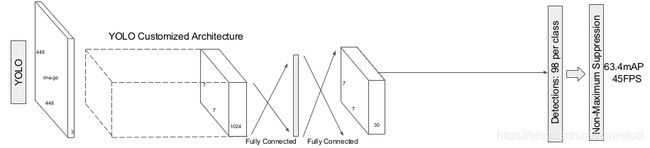
跳出具体的网络结构,我们从全局的观点来看看 YOLO v1 的结构。
从结构可以看出,YOLO v1 的整体结构很清晰,输入图片(448x448x3)经过 24 conv + 2 fc 后得到的 feature map size 为 1470x1,然后做了一个 reshape 操作,将 1470x1 reshape 为 7x7x30,所有的操作都没有什么特别之处。
只是为什么要做这个 reshape 操作了,这就是非常关键的一步了。具体可以参考下面的网络原理部分。
2 网络原理
上面已经提到, YOLO V1 中将检测任务视作一个回归任务,即 location 和分类的结果都是通过回归的方式得到。那么 YOLO V1 到底是如何工作的呢?
-
- 输入的图像被划分成 S×S 个网格单元。对于图像上出现的每一个目标,有一个网格单元(目标的中心落入的那个单元格)负责预测它。
-
- 每一个网格单元预测 B 个 bbox 以及 C 类概率。每个 bbox 预测结果有 5 个组成部分,分别是 ( x , y , w , h , c o n f i d e n c e ) (x,y,w,h,confidence) (x,y,w,h,confidence),其中 ( x , y ) (x,y) (x,y) 坐标代表 bbox 的中心的坐标值,坐标值是相对于对应的网格单元而言的,左上顶点坐标记为 0, 右下坐标记为 1(记住,如果框的中心不在网格单元内,那么这个单元格不负责检测这个目标),这些坐标被归一化到 0 到 1 之间。 ( w , h ) (w,h) (w,h) 框的尺寸也被归一化为 [ 0 , 1 ] [0,1] [0,1](相对于图像的大小)。confidence 的值,表示预测的 bbox 包含一个目标的置信度。计算公式为: P r ( O b j e c t ) × I O U ( p r e d , t r u t h ) Pr(Object)×IOU(pred, truth) Pr(Object)×IOU(pred,truth),从公式可以理解这个置信度衡量了两个方面:一个是 bbox 是否包含物体,另一个是 bbox 对于物体的位置预测的准确率(IOU)。如果一个 bbox 不包含物体,那么 P r ( O b j e c t ) Pr(Object) Pr(Object) 为 0, 即置信度为 0;如果一个 bbox 包含物体,那么 P r ( O b j e c t ) Pr(Object) Pr(Object) 为 1,置信度就是 bbox 和 ground truth box 的 IOU 值了。最后从 B 个 bbox 中选择 confidence 最大的那个作为最后的预测结果。
-
- 预测的时候输入一张图片,假设 S = 7,B = 2,C = 20,那么最后将得到 49 个 cell,每个 cell 对应 2 个 bbox,即 98 个bbox,每个 cell 对应输出一个 30(2x5+20)维的 tensor。98(7x7x2) 个 bbox, 对应输出 98 个 confidence 值。这里定义 class-specific confidence score 如下,这个 confidence score 将用来进行 NMS 操作。比如每个类别按照 confidence score 从大到小排序,对于同一个类别,如果 IOU 大于 0.5 就丢掉它对应的 bbox(避免重复检测同一个物体)。这里的 NMS 主要是针对预测较大的物体时,有可能出现多个区域预测同一个物体的情况。
c o n f i d e n c e = P r ( O b j e c t ) ∗ I O U ( p r e d , t r u t h ) confidence = Pr(Object)*IOU(pred, truth) confidence=Pr(Object)∗IOU(pred,truth)
c o n f i d e n c e _ s c o r e = P r ( C l a s s ( i ) ∣ O b j e c t ) ∗ c o n f i d e n c e = P r ( C l a s s ( i ) ∣ O b j e c t ) ∗ P r ( O b j e c t ) ∗ I O U ( p r e d , t r u t h ) = P r ( C l a s s ( i ) ∗ I O U ( p r e d , t r u t h ) confidence\_score = Pr(Class(i) | Object) * confidence = Pr(Class(i) | Object) * Pr(Object)*IOU(pred, truth) = Pr(Class(i)*IOU(pred, truth) confidence_score=Pr(Class(i)∣Object)∗confidence=Pr(Class(i)∣Object)∗Pr(Object)∗IOU(pred,truth)=Pr(Class(i)∗IOU(pred,truth)
- 预测的时候输入一张图片,假设 S = 7,B = 2,C = 20,那么最后将得到 49 个 cell,每个 cell 对应 2 个 bbox,即 98 个bbox,每个 cell 对应输出一个 30(2x5+20)维的 tensor。98(7x7x2) 个 bbox, 对应输出 98 个 confidence 值。这里定义 class-specific confidence score 如下,这个 confidence score 将用来进行 NMS 操作。比如每个类别按照 confidence score 从大到小排序,对于同一个类别,如果 IOU 大于 0.5 就丢掉它对应的 bbox(避免重复检测同一个物体)。这里的 NMS 主要是针对预测较大的物体时,有可能出现多个区域预测同一个物体的情况。
到这里就可以理解上面为什么要将 1470x1 reshape 为 7x7x30了。 30 是指 2x(4+1) + 20。这里 2 就是 上面的 B,4+1 是指每个 bbox 的预测值,包括 ( x , y , w , h , c o n f i d e n c e ) (x,y,w,h,confidence) (x,y,w,h,confidence),这里的 20 是 20 个类别对应的分类置信度(不包括背景)。
3 损失函数
YOLO 的损失函数由三部分组成,位置损失,置信度损失以及分类损失函数。
3.1 位置损失函数
L o s s 1 = λ c o o r d ∑ i = 0 S 2 ∑ j = 0 B Π i j o b j [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 ] + λ c o o r d ∑ i = 0 S 2 ∑ j = 0 B Π i j o b j [ ( w i − w ^ i ) 2 + ( h i − h ^ i ) 2 ] Loss_1 = \lambda_{coord} \sum_{i=0}^{S^2}\sum_{j=0}^{B}\Pi_{ij}^{obj}[(x_i-\hat{x}_i)^2+(y_i-\hat{y}_i)^2]+\lambda_{coord} \sum_{i=0}^{S^2}\sum_{j=0}^{B}\Pi_{ij}^{obj}[(\sqrt{w_i}-\sqrt{\hat{w}_i})^2+(\sqrt{h_i}-\sqrt{\hat{h}_i})^2] Loss1=λcoordi=0∑S2j=0∑BΠijobj[(xi−x^i)2+(yi−y^i)2]+λcoordi=0∑S2j=0∑BΠijobj[(wi−w^i)2+(hi−h^i)2]
其中
Π i j o b j = { 1 如 果 c e l l i 的 b b o x j 负 责 预 测 目 标 0 否 则 \Pi_{ij}^{obj} =\left\{ \begin{aligned} &1 \space如果 cell_i 的 bbox_j 负责预测目标\\ &0 \space 否则 \end{aligned} \right. Πijobj={1 如果celli的bboxj负责预测目标0 否则
对于位置损失,主要是计算 bbox 的 ( x , y , w , h ) (x,y,w,h) (x,y,w,h) 和对应的 ground truth box 的 ( x ^ , y ^ , w ^ , h ^ ) (\hat{x},\hat{y},\hat{w},\hat{h}) (x^,y^,w^,h^) 之间的 sum-squared error,需要注意的是并不是所有的 bbox 都参与 loss 的计算,首先必须是 c e l l i cell_i celli 中存在 object,并且 c e l l i cell_i celli 中的第 j 个 bbox 和 ground truth box 有最大的 IoU 值,那么这个 b b o x j bbox_j bboxj 才参与 loss 的计算,其他的不满足条件的 bbox 不参与。即,一个 ground truth box 只需要一个 bbox 来负责,而有最大 IoU 的 bbox 更接近 ground truth,所以学习起来更快。
对不同大小的box预测中,相比于大box预测偏一点,小box预测偏一点肯定更不能被忍受的。而sum-square error loss中对同样的偏移loss是一样。
为了缓和这个问题,作者用了一个比较取巧的办法,就是将 bbox 的 width 和 height 取平方根代替原本的 height 和 width。这个参考下面的图很容易理解,小 bbox 的横轴值较小,发生偏移时,反应到y轴上相比大 bbox 要大。
3.2 置信度损失函数
L o s s 2 = ∑ i = 0 S 2 ∑ j = 0 B Π i j o b j ( C i − C ^ i ) 2 + λ n o o b j ∑ i = 0 S 2 ∑ j = 0 B Π i j n o o b j ( C i − C ^ i ) 2 Loss_2 = \sum_{i=0}^{S^2}\sum_{j=0}^{B}\Pi_{ij}^{obj}(C_i-\hat{C}_i)^2 + \lambda_{noobj} \sum_{i=0}^{S^2}\sum_{j=0}^{B}\Pi_{ij}^{noobj}(C_i-\hat{C}_i)^2 Loss2=i=0∑S2j=0∑BΠijobj(Ci−C^i)2+λnoobji=0∑S2j=0∑BΠijnoobj(Ci−C^i)2
置信度损失的计算分两种情况,一种是有 object 的 cell 的置信度计算,另一种是没有 object 的 cell 的置信度计算。两种情况都是 cell 中所有的 bbox 都参与计算。对于有 object 的 cell 中的 bbox 的置信度的 ground truth 就是 1 ∗ I O U ( p r e d , t r u t h ) 1*IOU(pred,truth) 1∗IOU(pred,truth)。需要注意的是这个IOU是在训练过程中不断计算出来的,因为网络在训练过程中每次预测的 bbox 是变化的,所以 bbox 和 ground truth 计算出来的 IOU 每次也会不一样。而对于没有 object 的 cell 中的 bbox 的置信度的 ground truth 为 0 ∗ I O U ( p r e d , t r u t h ) = 0 0*IOU(pred,truth) = 0 0∗IOU(pred,truth)=0 ,因为不包含物体。
3.3 分类损失函数
L o s s 3 = ∑ i = 0 S 2 Π i o b j ∑ c ∈ c l a s s e s ( p i ( c ) − p ^ i ( c ) ) 2 Loss_3 = \sum_{i=0}^{S^2}\Pi_{i}^{obj}\sum_{c \in classes}(p_i(c)-\hat{p}_i(c))^2 Loss3=i=0∑S2Πiobjc∈classes∑(pi(c)−p^i(c))2
YOLO 中将分类损失当作回归来计算,使用 sum-squared error 来计算分类误差,需要注意的是只有包含 object 的 cell 才参与分类 loss 的计算,即 object 中心点落入的 cell 才进行分类 loss 的计算,而这个 cell 的 ground truth label 就是该物体的label。
3.4 overview
YOLO 有 3 种 loss,显然各种 loss 的重要程度是不一样的,所以各个 loss 有不同的权重。
- 首先在目标检测问题中,localization的误差比分类的误差更重要,所以给位置误差赋予更大的权重,记为 λ c o o r d = 5 \lambda_{coord} = 5 λcoord=5。
- 其次,因为一张图中大多数的 bbox 都是不包含目标的,那么这些 bbox 的 confidence 的 loss 就会产生比较大的影响,所以 λ n o o b j = 0.5 \lambda_{noobj} = 0.5 λnoobj=0.5,有目标的权重为 1。
总结起来就是:
- 对于有 object 的 cell,那么计算 cell 的分类误差,然后 cell 中两个 bbox 的置信度误差,然后 cell 中和 ground truth box 的 IoU 最大的 bbox 的位置误差。
- 对于没有 object 的 cell,那就只计算 cell 中两个 bbox 的置信度误差。
4 YOLO V1 的局限
- 因为 YOLO V1 中每个 cell 只预测两个 bbox 和一个类别,这就限制了能预测重叠或邻近物体的数量,比如说两个物体的中心点都落在这个 cell 中,但是这个 cell 只能预测一个类别。
- YOLO 是根据训练数据来预测 bbox 的(确切的说是对训练图像中目标的长宽比很依赖),但是当测试数据中的物体出现了训练数据中的物体没有的长宽比时,YOLO 的泛化能力就变弱了。
- 同时经过多次下采样,使得最终得到的 feature maps 的分辨率比较低,就是得到coarse feature,这可能会影响到物体的定位,导致定位不准。
- 损失函数的设计存在缺陷,使得物体的定位误差有点儿大,尤其在不同尺寸大小的物体的处理上还有待加强。
- 网络中有 fc 层,所以只能输入固定尺寸的图片。
当然 YOLO V1 的优势就是速度快,可以进行实时的检测,而且准确度也还不错。如下图所示。
参考
- Review On YOLOv1
- 目标检测 YOLO