机器学习笔记：受限玻尔兹曼机

本文整理自机器之心blog：
https://baijiahao.baidu.com/s?id=1599798281463567369&wfr=spider&for=pc

0x01 intro

受限玻尔兹曼机（RBM，Restricted Boltzmann machine）由多伦多大学的 Geoff Hinton 等人提出，它是一种可以用于降维、分类、回归、协同过滤、特征学习以及主题建模的算法。本质上是一种可用随机神经网络来解释的概率图模型。

随机指网络中的神经元是随机神经元，其输出状态只有两种（未激活和激活），状态的具体取值根据概率统计法则来决定。

0x02 预备知识

• sigmoid函数
• Bayes公式
• 二部图（bipartite graph）
• Monte-Calo方法：用样本均值逼近整体均值。但是，假定我们给定分布$p(x)$之后，如何进行采样？可以使用Markov链MC方法，使用马尔可夫链生成指定分布下的样本。
• 马尔可夫链
  可以在任何一本随机过程教材中找到。对于各态历经的马尔可夫链，存在唯一的平稳分布$\pi$：如果我们想在某个分布下采样，只需要模拟以其为分布的马尔可夫过程，最后样本分布会逐渐收敛到平稳分布。
• 正则分布
  一个物理系统如果有一定的自由度（例如一滴水的水分子可以在空间中任意排列），则系统中水分子的位置具有随机性。若系统处于状态$i$的概率为$p_i$，则必有
  $$\sum _i{p}_i=1$$
  不同的状态有不同的能量，记状态$i$的能量为$E_i$，由统计力学可知：当系统热平衡时，系统在状态$i$的概率$p_i$有下列形式：
  $$p_i=\frac{1}{Z_T}{e}^{-\frac{E_i}{T}}$$
  其中$Z_T$使得${\sum }_i{p}_i=1$。$T$为系统温度。这种概率分布称为正则分布。
  显然，给定温度下，能量小的状态有更高的概率，当$T\to \infty$时为均匀分布。
  在ML中，可以自定义能量函数，借鉴物理规律实现训练。
• Metropolis-Hastings采样和Gibbs采样

0x03 定义和结构

RBM 是两层神经网络，这些浅层神经网络是 DBN（深度信念网络）的构建块。RBM 的第一层被称为可见层或者输入层，它的第二层叫做隐藏层。

每一层由若干节点组成。相邻层之间是全连的，但是同层之间的节点是不相连的。也就是说，不存在层内通信，这就是受限波尔兹曼机中的限制所在。

每一个节点都是处理输入数据的单元，每个节点随机决定是否传递输入。随机意味着“随机判断”，这里修改输入（决定是否传递输入）的参数都是随机初始化的。

输入层（即可见层）以数据集样本中的低级特征作为输入。例如，对于一个由灰度图组成的数据集，每个输入节点都会接收图像中的一个像素值。MNIST 数据集中数据有 784 个像素点，所以处理它们的神经网络必须有 784 个输入节点。

获得输入之后，如下图所示，在隐藏层的节点 1，x 和一个权重相乘，然后再加上一个偏置项。这两个运算的结果可作为非线性激活函数的输入，在给定输入 x 时激活函数能给出这个节点的输出，或者信号通过它之后的强度。这里其实和我们常见的神经网络是一样的过程。

下图是多个节点相乘的情况：

因为所有可见（或输入）节点的输入都被传递到所有的隐藏节点了，所以 RBM 可以被定义为对称二部图，其中对称指每个隐藏节点都和每个可见节点两两相连。

0x04 重建（Reconstruction）

下面，我们会集中讨论它们如何以一种无监督的方式通过自身来重建数据，这使得在不涉及更深层网络的情况下，可见层和第一个隐藏层之间会存在数次前向和反向传播。

需要注意的是，和我们正常理解的神经网络不一样，RBM的每个节点（包括输入节点）都含有偏置项bias，因为这是正向/反向传播所需要的。

在重建阶段，第一个隐藏层的激活状态变成了反向传递过程中的输入。它们与每个连接边相同的权重相乘，就像 x 在前向传递的过程中随着权重调节一样。这些乘积的和在每个可见节点处又与可见层的偏置项相加，这些运算的输出就是一次重建，也就是对原始输入的一个逼近。这可以通过下图表达：

注意：上图中的每一个b各不相同。

因为 RBM 的权重是随机初始化的，所以，重建结果和原始输入的差距通常会比较大。你可以将 r 和输入值之间的差值看做重建误差，然后这个误差会沿着 RBM 的权重反向传播，以一个迭代学习的过程不断反向传播，直到达到某个误差最小值。

在前向传递过程中，我们可以看到，给定权重的情况下 RBM 会使用输入来预测节点的激活值，或者输出的概率：$P(a|x,w)$；但是在反向传递的过程中，当激活值作为输入并输出原始数据的重建或者预测时，RBM 会尝试在给定激活值 a 的情况下估计输入 x 的概率，它具有与前向传递过程中相同的权重参数，即：$P(x|a,w)$。这两个概率估计将共同得到关于输入 x 和激活值 a 的联合概率分布，或者 $P(x,a)$。

这里说的重建与回归有所不同，也不同于分类。回归基于很多输入来估计一个连续值，分类预测出离散的标签以应用在给定的输入样本上，而重建是在预测原始输入的概率分布。

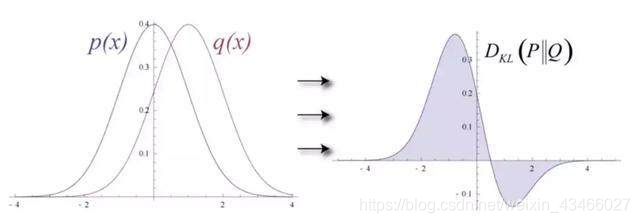
这种重建被称之为生成学习，它必须跟由分类器执行的判别学习区分开来。判别学习将输入映射到标签上，给定一个输入x的话，输出就是$P(y|x)$。若假设 RBM 的输入数据和重建结果是不同形状的正态曲线，它们只有部分重叠。

为了衡量输入数据的预测概率分布和真实分布之间的距离，RBM 使用 KL 散度来度量两个分布的相似性。KL 散度测量的是两条曲线的非重叠区域或者说发散区域，RBM 的优化算法尝试最小化这些区域，所以当共享权重与隐藏层的激活值相乘时就可以得出原始输入的近似。图的左边是一组输入的概率分布 p 及其重构分布 q，图的右侧是它们的差的积分。

0x05 概率分布

在一个随机生成的灰度图中，每一个像素的取值都是均匀的。但是在MNIST数据集的灰度图中，每一个像素的取值概率又是不均匀的。在黑白人像的灰度图中，我们又可以发现每一个像素的取值概率还是不均匀的。因此，使用人像的概率分布来拟合MNIST数据集的概率分布就会有较大的差异。

或者举另一个例子：语言是字母的特定概率分布，因为每一种语言会使用一些字母较多，而另一些较少。在英语中，字母 e、t 以及 a 是最常见的，然而在冰岛语中，最常见的字母是 a、t 和 n。因此尝试使用基于英语的权重集合来重建冰岛语将会导致较大的差异。

想象一下仅输入狗和大象图片的 RBM，输入层为x，仅两个输出节点a1和a2，一个结点对应一种动物。在前向传递的过程中 RBM 会问自己这样的问题：在给定的这些像素下，我应该向哪个节点发送更强的信号呢，大象节点还是狗的节点？在反向传递的过程中 RBM 的问题是：给定一头大象的时候，应该期望那种像素分布？

这就是联合概率分布：给定 a 时 x 的概率以及给定 x 时 a 的概率，可以根据 RBM 两层之间的共享权重而确定。

从某种意义上而言，学习重建的过程就是学习在给定的图像集合下，哪些像素会倾向于同时出现。

这些重建代表着 RBM 的激活值所「认为」输入数据看起来的样子，Geoff Hinton 将其称为机器「做梦」。当被呈现在神经网络在训练过程时，这种可视化是非常有用的启发，它让人确信 RBM 确实在学习。如果不是，那么它的超参数应该被调整。

最后一点：你会注意到 RBM 有两个偏置项。这是有别于其它自动编码器的一个方面。隐藏层的偏置项有助于 RBM 在前向传递中获得非零激活值，而可见层的偏置有助于 RBM 学习后向传递中的重建。