处理多目标优化
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 案例一 利用GA方法求解多目标优化
-
- 1.代码如下
- 案例二 如将多目标寻优转化为单目标寻优
前言
提示:这里可以添加本文要记录的大概内容:
在工程领域,存在着大量的多目标优化的问题。这类问题的共同特征是需要在复杂且庞大的搜索空间去寻求最优解,有时候也会考虑到算法的时间复杂度就会把多目标优化问题通过隶属度函数转化成单目标优化。(本文参考了智能优化30案例 chap9,与许老师的最优化方法)
提示:以下是本篇文章正文内容,下面案例可供参考
案例一 利用GA方法求解多目标优化
示例:pandas 是基于NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。
1.代码如下
MGA对多目标函数的寻优 其注意f(1)、f(2)优化的返回值和x(1)、x(2)、x(3),其与单目标优化的最大的区别终于其返回值设定了多个。(f(1)、f(2));
function f = my_first_multi(x)
%优化的目标函数
%f(1)=-(23.5649-1.4948*x(1)-0.2318*x(2)-2.2687*x(3)+0.0308*x(2)^2+0.0054*x(2)^2+0.3805*x(3)^2)/7.8727;
%f(2)=(0.0375*x(3)+0.6545)/0.15;
f(1)=4413-437.34*x(1)-280.11*x(2)-303.28*x(3)+72.42*x(1)*x(2)-34*x(1)*x(3)-4.7*x(2)*x(3)+74.66*(x(1)^2)-53.24*(x(2)^2)-9.36*(x(3)^2);
f(2)=4.18+0.085*x(1)+0.001*x(2)+0.031*x(3)+1*0.0001*x(1)*x(2)+8.5*0.003*x(1)*x(3)-5.0*0.00005*x(2)*x(3)-1.417*0.003*x(1)^2+1.533*0.003*x(2)^2-1.667*0.00001*x(3)^2;
###2.
主函数的代码如下 其调用了matlab优化工具箱函数(GA)
clear
clc
fitnessfcn = @my_first_multi; % Function handle to the fitness function
nvars = 3; % Number of decision variables
lb = [4,1,9]; % Lower bound
ub = [7,5,15]; % Upper bound
A = []; b = []; % No linear inequality constraints
Aeq = []; beq = []; % No linear equality constraints
options=gaoptimset('ParetoFraction',0.3,'PopulationSize',100,'Generations',200,'StallGenLimit',200,'TolFun',1e-100,'PlotFcns',@gaplotpareto);
[x,fval] = gamultiobj(fitnessfcn,nvars, A,b,Aeq,beq,lb,ub,options);
该处使用的url网络请求的数据。
案例二 如将多目标寻优转化为单目标寻优
在处理优化多个目标且每个每个优化对象有其响应的指标。而且还想转换成单目标优化问题,可以借鉴以下的隶属度函数来设定权值。
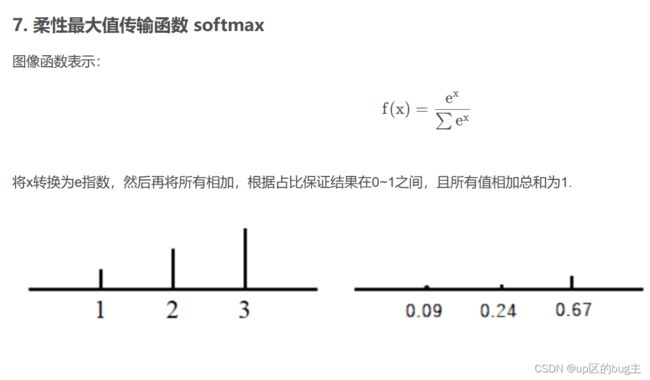
比如工程要求其指标误差在2%以内,通过误差的大小来设定其指标的重要性,那就可以在暴力寻优的过程中加入个分段函数,在指标值超过2%的时候就设定值比较的函数。在学习神经网络的时候会有神经网络传递函数的概念,其可以引入其传递函数来设定其隶属度函数。
(此处借鉴了https://blog.csdn.net/weixin_41218229/article/details/124730175?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166417465616782248531196%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=166417465616782248531196&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduend~default-2-124730175-null-null.142v50pc_rank_34_2,201v3control_2&utm_term=%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E4%BC%A0%E9%80%92%E5%87%BD%E6%95%B0&spm=1018.2226.3001.4187)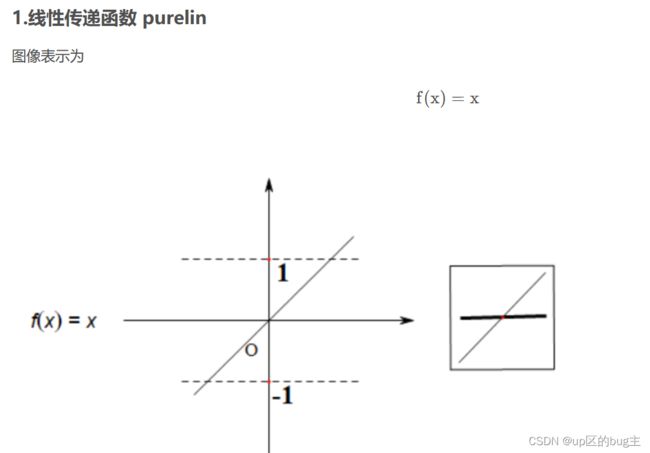
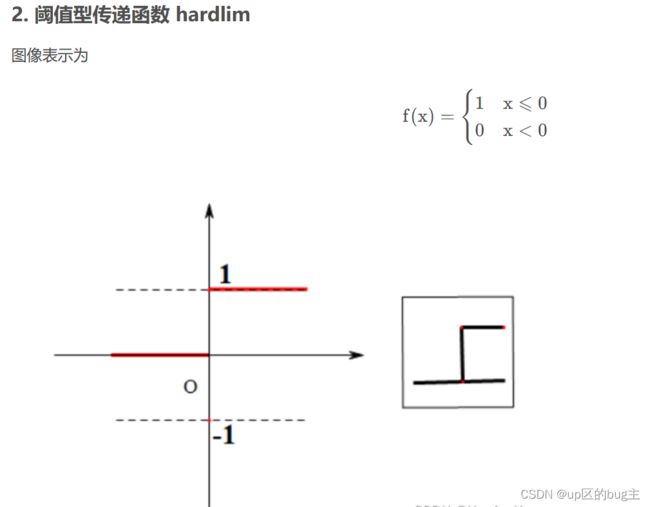
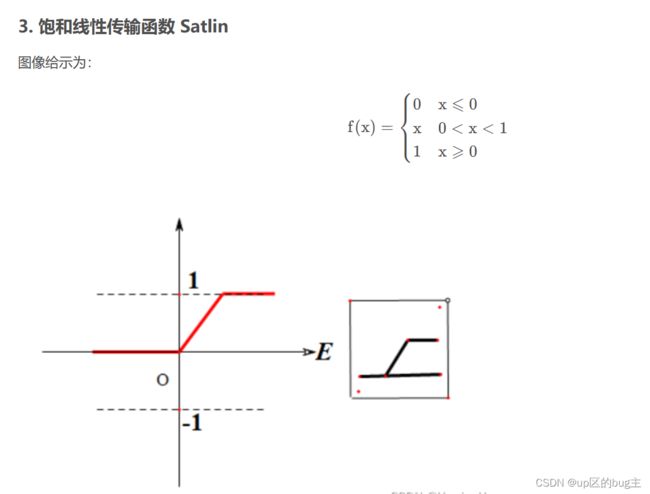
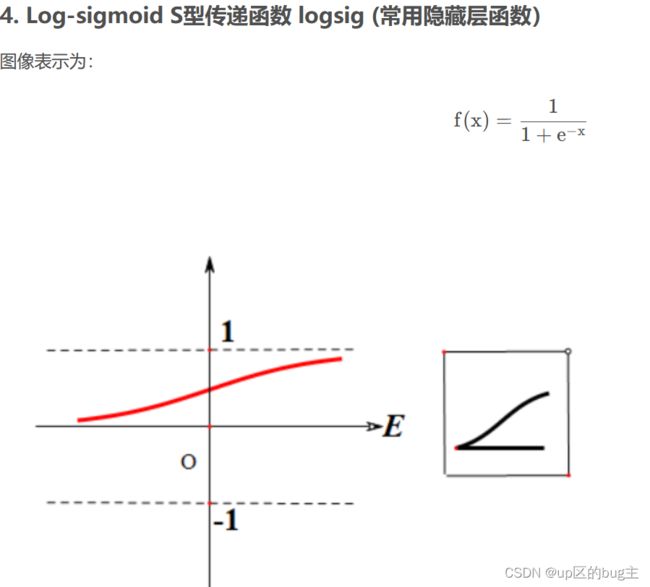
。