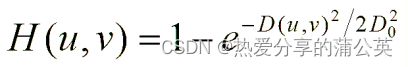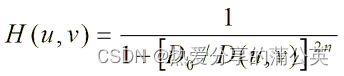读入一幅图像，对图像分别进行高斯低通、巴特沃兹低通、高斯高通和巴特沃兹高通频域滤波，比较其锐化和平滑效果。

  ↵

1、高斯低通

        二维高斯低通滤波器定义如下：

 

        D0为截止频率与原点的距离，D(u,v)是点(u,v)与原点的距离。

        图像表示：

         读入图片并得到频谱图，后续搭建高斯低通滤波器如下。

[m,n]=size(image_fft_shift);%获得图像的高度和宽度
H_Gassian_low_pass_filter=zeros(m,n);%滤波器函数
a0=m/2;%图像中心点
b0=n/2;
D0=10;%截至频率距离圆点的距离
delta=D0;%delta表示高斯曲线的扩散程度
for x=1:m
   		for y=1:n 
        	d=(x-a0)^2+(y-b0)^2;%计算点（x,y）到中心点的距离
        %计算高斯滤波器
H_Gassian_low_pass_filter(x,y)=exp(-d/(2*delta^2));  
    	end
end
%滤波后结果
image_res=H_Gassian_low_pass_filter.*image_fft_shift;
image_new=uint8(real(ifft2(ifftshift(image_res))));
subplot(2,2,3),imshow(image_new);
title('高斯低通滤波所得图像'); 
subplot(2,2,4),imshow(H_Gassian_low_pass_filter);
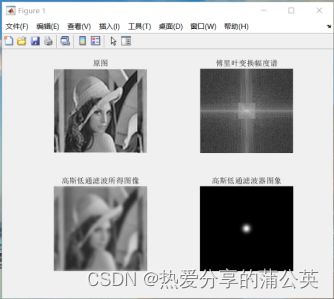
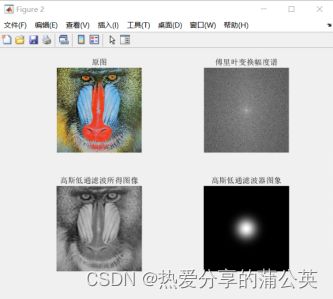
title("高斯低通滤波器图象");

        测试结果如图所示。

图6.1 对图像进行高斯低通滤波测试结果（D0=10）

图6.1 对图像进行高斯低通滤波测试结果（D0=20）

 

 图6.1 对图像进行高斯低通滤波测试结果（D0=40）

 

2、巴特沃兹低通

        n阶巴特沃兹低通滤波器定义如下：

         D0为截止频率与原点的距离，D(u,v)是点(u,v)与原点的距离.

        图像表示：

        特点：

1. 不同于理想低通滤波器，BLPF在通带与被滤除的频率之间没有明显的截断
2. 当D(u,v)=D0时，H(u,v)=0.5；当D(u,v)=0时，滤波器取最大值1
3. 巴特沃兹滤波器阶数越高，越趋近于理想低通滤波器

        读入图片并得到频谱图一，后续搭建巴特沃兹低通滤波器如下。

[m,n]=size(image_fft_shift);%获得图像的高度和宽度
H_Butterworth_low_pass_fliter=zeros(m,n);%滤波器函数
a0=m/2; b0=n/2; %图像中心点
D_Butterworth_low_pass=40;
N_Butterworth_low_pass=1; %巴特沃兹滤波器的阶数
for x=1:m
    	for y=1:n
        	distance=sqrt((x-a0)^2+(y-b0)^2);
            H_Butterworth_low_pass_fliter(x,y)=1/(1+(distance/D_Butterworth_low_pass)^(2*N_Butterworth_low_pass));
    	end
end
image_res_Butterworth_low_pass=H_Butterworth_low_pass_fliter.*image_fft_shift;
image_new_Butterworth_low_pass=uint8(real(ifft2(ifftshift(image_res_Butterworth_low_pass))));
subplot(2,2,3),imshow(image_new_Butterworth_low_pass);
title('巴特沃兹低通滤波所得图像'); 
subplot(2,2,4),imshow(H_Butterworth_low_pass_fliter);
title("巴特沃兹低通滤波器图象");

3、高斯高通

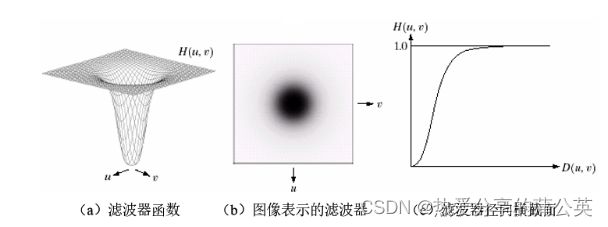
        二维高斯高通滤波器定义如下：

 

        D0为截止频率距原点的距离，D(u,v)是点(u,v)距原点的距离。

        图象表示：

         读入图片并得到频谱图，后续搭建高斯高通滤波器如下，与高斯低通滤波器类似，只是H（u,v）发生了变化。

[m,n]=size(image_fft_shift);%获得图像的高度和宽度
H_Gassian_high_pass_filter=zeros(m,n);%滤波器函数
%图像中心点
a0=m/2;			b0=n/2;
D_gassian_high_pass=10;%截至频率距离圆点的距离
delta_gassian_high_pass=D_gassian_high_pass;%delta表示高斯曲线的扩散程度
for x=1:m
   		for y=1:n
        	d=(x-a0)^2+(y-b0)^2; %计算点（x,y）到中心点的距离
        	%计算高斯滤波器
        	H_Gassian_high_pass_filter(x,y)=1-exp(-d/(2*delta_gas sian_ high_pass^2));
    	end
end
%滤波后结果
image_res_gassian_high_pass=H_Gassian_high_pass_filter.*image_fft_shift;
image_new_gassian_high_pass=uint8(real(ifft2(ifftshift(image_res_gassian_high_pass))));
subplot(2,2,3),imshow(image_new_gassian_high_pass);
title('高斯高通滤波所得图像'); 
subplot(2,2,4),imshow(H_Gassian_high_pass_filter);
title("高斯高通滤波器图象");

4、巴特沃兹高通

        n阶巴特沃兹高通滤波器定义如下

 

        D0为截止频率距原点的距离，D(u,v)是点(u,v)距原点的距离。

        图像表示：

        读入图片并得到频谱图，后续搭建巴特沃兹高通滤波器如下，过程与巴特沃兹低通滤波器类似，只是函数发生了变化。

[m,n]=size(image_fft_shift);%获得图像的高度和宽度
H_Butterworth_high_pass_filter=zeros(m,n);%滤波器函数
a0=m/2;
b0=n/2;%图像中心点
D_Butterworth_high_pass=40;
N_Butterworth_high_pass=10;%巴特沃斯滤波器的阶数
for x=1:m
    	for y=1:n
        	distance=sqrt((x-a0)^2+(y-b0)^2);
            H_Butterworth_high_pass_fliter(x,y)=1/(1+(D_Butterworth_high_pass/distance)^(2*N_Butterworth_high_pass));
    	end
end
%滤波后结果
image_res_Butterworth_high_pass=H_Butterworth_high_pass_fliter.*image_fft_shift;
image_new_Butterworth_high_pass=uint8(real(ifft2(ifftshift(image_res_Butterworth_high_pass))));
subplot(2,2,3),imshow(image_new_Butterworth_high_pass);
title('巴特沃兹高通滤波所得图像'); 
subplot(2,2,4),imshow(H_Butterworth_high_pass_fliter);
title("巴特沃兹高通滤波器图象");

5、四种滤波比较

        总的来说，低通滤波器可以起到平滑作用，高通滤波器可以起到锐化作用。通过观察测试结果可以进一步得出下列结论。

滤波器	性能比较
高斯低通滤波器	随着截止频率的增大，平滑效果越来越弱；平滑效果稍差于相同截止频率的二阶巴特沃兹低通滤波器；过渡特性非常平坦，没有出现振铃现象。
巴特沃兹低通滤波器	随着滤波器半径（截止频率）的增大，平滑效果越来越弱；随着阶数增加，越来越趋近于理想低通滤波器；低阶滤波器没有明显振铃现象（滤波器在低频和高频之间平滑过渡），阶数越高，滤波器的过度越剧烈，振铃现象将越明显。
高斯高通滤波器	高斯高通滤波的结果比巴特沃兹高通滤波的结果更尖锐，即使是对微小物体和细线条的滤波也是较清晰的。
巴特沃兹高通滤波器	巴特沃兹高通滤波的结果比高斯高通滤波的结果平滑一些。

---

 很高兴您能看到这里，文中提到的一些函数如果有不懂可以留言也可以在matlab支持(支持 - MATLAB & Simulink (mathworks.cn))里去查询。希望本文对您学习有所帮助！