逻辑回归模型混淆矩阵评价与ROC曲线最佳阈值的好处（附Accuracy,TPR,FPR计算函数）

一、得到阈值在0.5和0.8下模型的混淆矩阵

y_prob=result.predict(X_test)#得到概率值

y_predict1=pd.DataFrame(y_prob>0.5).astype(int)#用0.5作为阈值判断
y_predict2=pd.DataFrame(y_prob>0.8).astype(int)

from sklearn import metrics
a_05=metrics.confusion_matrix(y_test,y_predict1,labels=[0, 1])
plt.figure(dpi=125)
sns.heatmap(a_05,annot=True,fmt='.20g', xticklabels= True, yticklabels= True, square=True, cmap="YlGnBu")#fmt='.20g'取消科学计数法
plt.title('0.5阙值混淆矩阵')
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.show()

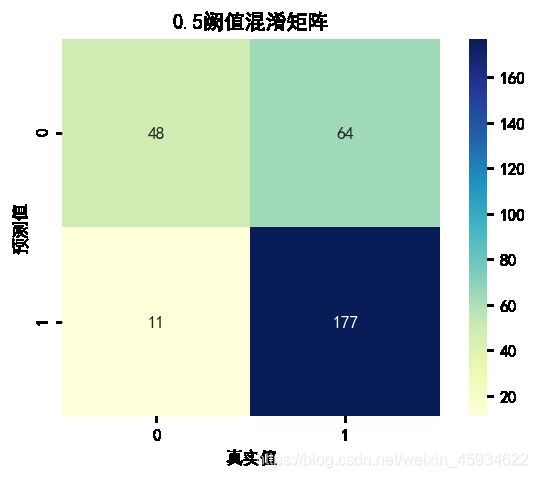
由于在该数据集中，0代表未能按期还款，1代表按期还款。根据该模型测试集产生的混淆矩阵可以发现：当阙值设为0.5时，在模型预测为1的数据中，实际为1的数据有177条，远多于实际为0数据的11条。可见对1的预测效果非常好。但在预测为0的数据中，实际为0的数据有只有48条，少于实际为1数据的64条，明显对0的预测效果并不好。总之在0.5阈值下，模型对按期还款的客户预测效果非常好，但对未能按期还款客户的预测效果并不好。

a_08=metrics.confusion_matrix(y_test,y_predict2,labels=[0, 1])
plt.figure(dpi=125)
sns.heatmap(a_08,annot=True,fmt='.20g', xticklabels= True, yticklabels= True, square=True,cmap="YlGnBu")#,fontproperties=prop)
plt.title('0.8阙值混淆矩阵')
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.show()

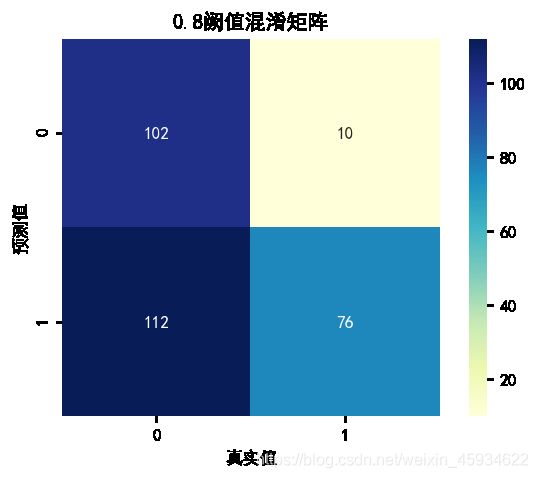
根据该模型测试集产生的混淆矩阵可以发现，当阙值设为0.8时，在模型预测为1的数据中，实际为1的有76条，少于实际为0的112条数据。可见对1的预测效果非常不好。在预测为0的数据中，实际为0的数据有102条，远多于实际为1数据的10条，明显对0的预测效果非常好。总之在0.8阈值下，模型对未能按期还款客户的预测效果非常好，但对按期还款客户的预测效果并不好。

		   准确率     TPR	FPR
	0.5阈值	0.75	 0.94	0.57
	0.8阈值	0.59	 0.43	0.09

进行进一步的计算，得出模型在0.5阈值和0.8阈值下模型的准确率、TPR和FPR。理论上准确率越高，TPR越高，且FPR越低的模型，模型的精度越高。可以发现在0.5阈值下，TPR高到0.94，但FPR也高到0.57，模型阈值在0.8时，FPR低到0.09，但TPR也跌到了0.43。两个阈值都不是非常理想。但相对而言，0.5阈值的准确率较高。在其他条件相同的情况下，会选择0.5阈值的模型。

二、绘制ROC曲线

plt.figure(dpi=100)
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_prob, pos_label=1)
auc='AUC值：'+str(round(metrics.roc_auc_score(y_test, y_prob),3))
plt.plot(fpr, tpr) #绘制ROC曲线图
plt.text(x=0.4,y=0.45,s=auc)
plt.xlabel("FPR") 
plt.ylabel("TPR")
plt.title("ROC_Line")
plt.show()

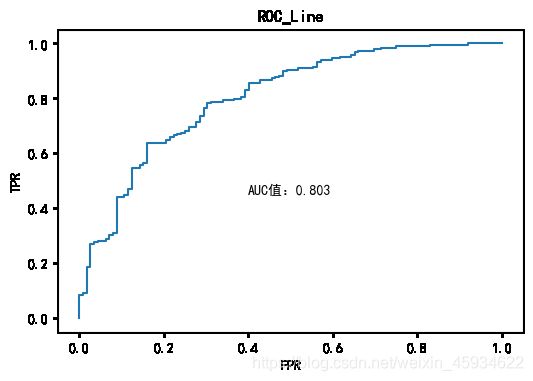
如ROC曲线图，ROC曲线横轴为正确预测的比率(TPR)，纵轴为错误预测的比率(FPR)，在该曲线中，可以发现用来建立该模型的数据量较少，导致了FPR在0.2以内的变换率不稳定。对薪资、微博好友数进行对数变换，以及将消费理念这种均匀分布的数据按照中位数进行数据离散化处理后。该模型在测试集的预测得出的，根据该模型ROC曲线上下的面积，计算出改模型的AUC值达到0.803，略大于一般要求的0.8，又因为是在测试集得出的结果，可以说明该模型的泛化能力较强。可以总结出，AUC值反映的是模型的预测能力，取值是阈值无关的。

三、利用KS曲线得到最佳阈值

#绘制KS曲线
plt.figure(dpi=100)
plt.plot(thresholds,fpr)
plt.plot(thresholds,tpr)
plt.text(x=0.656,y=0.89,s='最大KS为：'+str(round(KS_max,3))+'>0.4')
plt.text(x=0.656,y=0.82,s='最佳阈值为：'+str(round(best_thr,3)))
plt.plot([0.656,0.656],[0.304,0.782], 'r--')
plt.xlabel("thresholds") 
plt.ylabel("fpr/tpr")
plt.title("KS_Line")
plt.xlim(0,1)
plt.show()

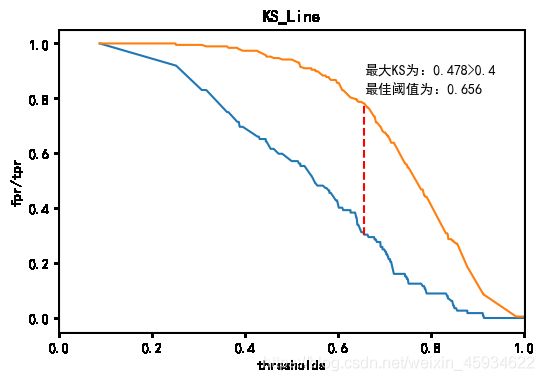
根据该模型预测概率计算出的TPR和FPR绘制出图4KS曲线，经过计算，得出最大KS为0.487，大于一般要求的0.4。并同样得出最佳阈值约为0.656。可以根据这一最佳阈值，在预测概率上划分出最合适的0和1，得出模型最佳的预测结果和对应的混淆矩阵。

四、最佳阈值的比较

plt.figure(dpi=100)
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_prob, pos_label=1)
plt.annotate('0.5阈值', (0.571,0.941), xytext=(10, -28),textcoords='offset points', arrowprops=dict(facecolor='#8b8b8b',arrowstyle='fancy'))
plt.annotate('0.8阈值', (0.089,0.404), xytext=(20, -20),textcoords='offset points', arrowprops=dict(facecolor='#8b8b8b',arrowstyle='fancy'))
plt.annotate('0.656最佳阈值', (0.304,0.777), xytext=(10, -35),textcoords='offset points', arrowprops=dict(facecolor='#8b8b8b',arrowstyle='fancy'))
plt.xlabel("FPR") 
plt.ylabel("TPR")
plt.title("ROC_Line")
plt.show()

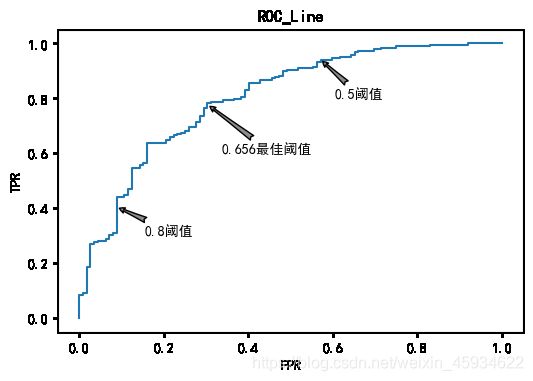
可以发现最佳阈值模型的TPR明显高于0.5阈值模型的TPR，且其FPR也明显低于0.8阈值模型的FPR。最佳阈值模型的准确率达到0.75，维持在较高的水平。非常符合阈值TPR高，且FPR低以及准确率越高的模型选取原则。因此模型在最佳阈值下，对按期还款和未能按期还款的预测效果要更好，更具有代表性，其业务价值更高。

四、最佳阈值的选择

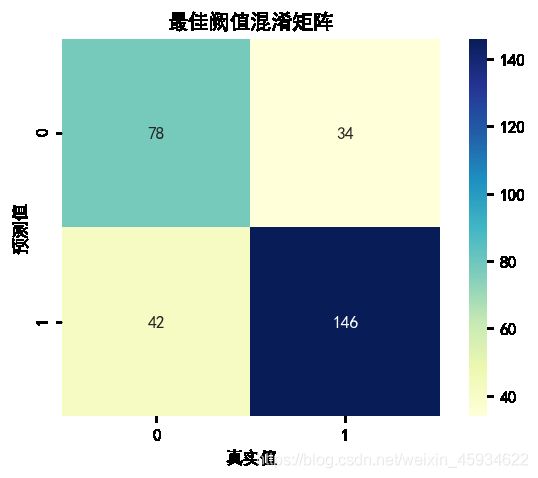
根据该模型测试集产生的混淆矩阵可以发现，当阙值设为最佳阈值时，在模型预测为1的数据中，实际为1的有146条，远多于实际为0数据的42条。可见对1的预测效果非常好，在预测为0的数据中，实际为0的数据有78条，是实际为1数据的两倍多，对0的预测效果也比较好。在最佳阈值下，该模型对按期还款和未能按期还款的预测都非常好。

• 附Accuracy,TPR,FPR计算函数
  带入的是混淆矩阵得到数组：a_05=metrics.confusion_matrix(y_test,y_predict1,labels=[0, 1])

def pr(a):
    accuracy=round((a[1][1]+a[0][0])/(a[1][0]+a[1][1]+a[0][0]+a[0][1]),3)#准确率  accuracy=(TP+TN)/(P+N) 预测正确的样本数目/参加预测的样本总数目
    TPR=round(a[1][1]/(a[1][0]+a[1][1]),3)#它表示所有预测为1的样本中真正为1的比例。此外,它也被称为灵敏度或召回率,如TPR=TP/(TP + FN) 
    FPR=round(a[0][1]/(a[0][0]+a[0][1]),3)#它表示错误预测了所有负值中有多少负值。其计算公式为：FPR =FP/（FP + TN)
    return(accuracy,TPR,FPR)

• 模型和学习笔记系列1_END

点赞和收藏是周更的动力，真心谢谢！

欢迎交流和讨论，有偿纠错。