VAE论文解读及代码实现

1.Introduction

Variational Autoencoders (VAEs) 是一种无监督学习复杂分布的方法，VAEs已经显示出产生多种复杂数据的潜力，包括手写数字，面部，门牌号码，CIFAR图像，场景的物理模型和分割以及从静态图像预测未来。
生成模型是机器学习一个很广泛的领域，求高维空间的X的分布P(x)，比如，图像就是一种可以创建生成模型的数据类型，每一幅图像都有成千上万的维度（元素），成模型的工作是以某种方式捕获像素之间的依赖关系，例如附近的像素具有相似的颜色并将其组织为对象。

2.VAE AutoEncoder

$P(X|Z)$是一个isotropic Gaussian,即$P(X|Z)$~$N(f(Z;\theta ),{\sigma }^{2}I)$ ，$I$为单位矩阵，$f(z;\theta )$为均值，${\sigma }^{2}I$为协方差矩阵。$-logP(X|Z)$和f(Z)与X的欧式距离的平法成比例,$-log\frac{1}{\sqrt{2}\ast \pi }$为一常数不影响概率比较,证明公式如下：
$$-logP(X|Z)=-\sum _{i=1}^{n}log(P(X_i|Z)=\sum _{i=1}^n-log\frac{1}{\sqrt{2}\ast \pi }+\frac{(X^{(1)}-f(Z{)}^{(i)}{)}^2}{2{\delta }^2}$$
$$||f(Z),X|{|}^2=\sum _{i=1}^n(f(Z{)}^{(i)}-X^{(i)}{)}^2$$

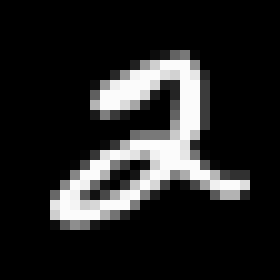
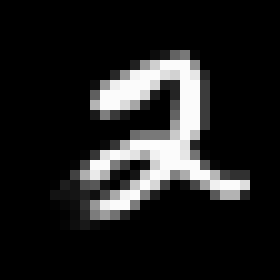
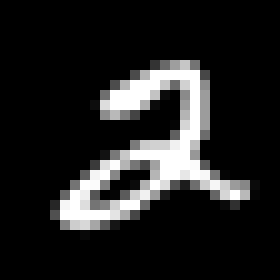
上图中左边的那个是真实样本，中间和右边的图片都是生成的图片，看起来中间的图生成的更差，但是分别与原始样本求欧式距离，右边的比中间的大，因为右边的图像相较于原始样本每一个像素都向右下移了半个像素，如果我们想设置一个特别小的$\sigma$让生成中间图的这种错误不对训练P(X)有帮助，但同样虽然右边的和原始样本几乎一样也会被拒绝。
在实际中，大部分的$P(X|z)$趋近于0,反响传播误差时，P(X|z)的训练缓慢，且对$P(X)=\int P(X|z)P(z)dz$的提升无太大影响，我们需要一个新的函数$Q(Z|X)$~$N(\mu (X),{\sigma }^2(x)I)$，而$P(z|X)$表示经过解码以后恢复成X概率较大的z服从的一个理想分布。我们要让Q(z|X)无线趋近P(z|X)。
接下来我们需要把$E_{z～Q}P(X,z)$和$P(X)$联系起来，即将出现变分子编码器的核心公式了：
$$logP(X)-D[Q(z|X)||P(z|X)]=Ez\sim Q[logP(X|z)]-D[Q(z|X)||P(z)].(1)$$
$logP(X)$是我们需要最大化的目标函数，$D[Q(z|X)||P(z|X)]$当z趋向于重现X时，这一项趋向于0，我们需要指定Q(z|X)的分布，一般指定为正态分布，即$Q(z,X)$~$N(\nu (X;\theta ),\sum (X;\theta ))$，$\nu$和$\sum$的参数可以通过神经网络学习到，故后面将其省略，$\sum$是一个主对角矩阵,给我们计算右边的式子提供了方便。右边第二项$D[Q(z|X)||P(z)]$变成了两个多维高斯分布的KL-散度，$$D[N(\mu (X),\Sigma (X))||N(0,I)]=\frac{1}{2}(tr(\sum (X)+(\nu (x){)}^T-k-logdet(\sum (X)))（2）$$
公式推到如下：由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可，根据定义我们可以写出：
$$KL(N(\mu ,{\sigma }^2),N(0,1))=\int \frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\nu {)}^2}{2{\sigma }^2}}(log\frac{1}{\sqrt{2\pi }\sigma }-\frac{(x-\nu {)}^2}{2{\sigma }^2}+log\frac{1}{\sqrt{2\pi }}-\frac{x^2}{2})$$
$$=\frac{1}{2}\int \frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\nu {)}^2}{2{\sigma }^2}}(-log{\sigma }^2+x^2-\frac{(x-\nu {)}^2}{{\sigma }^2})$$
第一项实际上就是$-log{\sigma }^2$乘以概率密度的积分（也就是1），所以结果是$-log{\sigma }^2$；第二项实际是正态分布的二阶原点矩，$E(X^2)=E(x{)}^2+D(X)={\nu }^2+{\sigma }^2$；而根据定义，第三项实际上就是“-方差除以方差=-1”。所以结果就是：
$$KL(N(\mu ,{\sigma }^2),N(0,1))=\frac{1}{2}(-log{\sigma }^2+{\nu }^2+{\sigma }^2-1)（3）$$
考虑以下三个话题：
a.除了$logP(X)$，优化项$D[Q(z|X)||P(z,X)]$的引入带来了多少估计误差。
b.用信息论来解释VAEs框架（尤其是等式（1）的右边）
c.VAE是否存在稀疏自编吗器相似的正则化项（罚项）
$D[Q(z|X)|P(z|X)]>=0$，故等式右边是$log(X)$的一个下界，我们可以通过优化右边来优化左边，$P(X|z)(X|f(z),{\sigma }^{2}I)$中的sigma对应稀疏自编玛器中的$\lambda$,控制编码器与标准正态分布的KL散度和最大化logP(X|z)间的一个平衡。
3.代码解读与实现
编码器是一个五层的全连接网络，对应于拟合Q(z|X)接近标准正态分布，最后一层的维数为隐变量z的维数乘2，因为z通过$\sigma$和$\mu$来进行抽样，解码器也是一个五层的全连接神经网络，对应于拟合P(X|z)。
接下来我们开始实现基于mnist数据集的变分自编玛器，首先导入必要包，然后开始构建一个class，这个类包含一个构造函数和一些其他成员函数，先来实现构造函数：

    def __init__(self, latent_dim, batch_size, encoder, decoder,
                 observation_dim=784,
                 learning_rate=1e-4,
                 optimizer=tf.compat.v1.train.RMSPropOptimizer,
                 observation_distribution="Gaussian", # or Gaussian
                 observation_std=0.01):
                 
        self._latent_dim = latent_dim#隐藏层z的维度
        self._batch_size = batch_size#一次训练样本的大小
        self._encode = encoder
        self._decode = decoder
        self._observation_dim = observation_dim#输入，输出维度
        self._learning_rate = learning_rate
        self._optimizer = optimizer(learning_rate=self._learning_rate)
        self._observation_distribution = observation_distribution#隐变量Z分布
        self._observation_std = observation_std#上文提到的超参数sigma
        self._build() 

接下来开始构建神经网络，编码器的输出是隐变量z的维数的两倍的一个向量，前面一半用来拟合$\nu (X)$，后面一半用来拟合$log\sigma (X)$，用重参数技巧($z=epsilon\ast \sigma +\nu$,其中epsilon~$N(0,1)$),得到z。z作为解码器的输入得到输出obs_mean(即$f(z)$)，$P(X|z)=N(X|f(z);\sigma \ast I)$，则$logP(X|z)$就可以求出，加上式（3）导出的计算$KL(Q(z|X),N(0,1))$的公式即为我们要训练的模型的损失函数。

    def _build(self):
        self.x=tf.placeholder(tf.float32,(None,self._observation_dim))
        with tf.variable_scope('encoder'):
            encoded=coders.vae_coding.fc_mnist_encoder(self.x,self._latent_dim)
            logvar=encoded[:,self._latent_dim:]
            self.mean=encoded[:,:self._latent_dim]
            epsilon=tf.random.normal((self._batch_size,self._latent_dim))
            self.z=epsilon*tf.sqrt(tf.exp(logvar))+self.mean
        with tf.variable_scope('decoder'):
            self.obs_mean=coders.vae_coding.fc_mnist_decoder(self.z,self._observation_dim)
        with tf.variable_scope('loss'):
            objective=self._gaussian_log_likelihood(self.x,self.obs_mean,self._observation_std)
            kl=self._kl_diagnormal_stdnormal(self.mean,logvar)
            self._loss=(objective+kl)/self._batch_size
            self._train=self._optimizer.minimize(self._loss)
        self._sess=tf.Session()
        self._sess.run(tf.global_variables_initializer())

全部代码连接github