VAE粗略理解

AE

自编码是一种表示学习的技术，是deep learning的核心问题

让输入等于输出，取中间的一层作为embedding， 即编码

对中间的隐层进行约束，就可以得到不同类型的编码

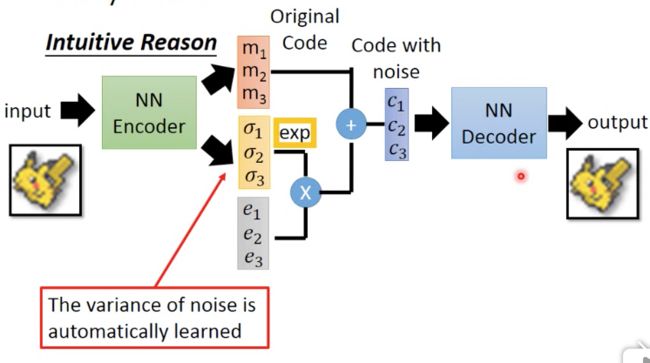
h

h>x, 并且约束其稀疏性，就得到稀疏编码

自编码网络，可以理解为，

完成训练后，Decoder部分就没有用了

 

SAE

堆叠自编码器

 

 

各种自编码的变形

 

VAE的差别

和普通autoencoding比，

VAE的Encoder会输出两个向量，你可以把其中一个看成mean，另一个看成variance,还加入一个误差error，这个error是从一个高斯分布sample出来的（额外的loss,原文中KL散度计算正态与标准正态）

最终把这3个向量合成成code(variance要乘上一个noise，这个噪声来模拟取样，然后加在mean上)

 

 

 

VAE漫谈

变分自编码器

分布变换

通常我们会拿 VAE 跟 GAN 比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量 Z 生成目标数据 X 的模型，但是实现上有所不同。

更准确地讲，它们是假设了服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 X=g(Z)，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式。

那现在假设服从标准的正态分布，那么我就可以从中采样得到若干个 Z1,Z2,…,Zn，然后对它做变换得到 X̂1=g(Z1),X̂2=g(Z2),…,X̂n=g(Zn)，我们怎么判断这个通过 f 构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？

有读者说不是有 KL 散度吗？当然不行，因为 KL 散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式。

我们只有一批从构造的分布采样而来的数据 {X̂1,X̂2,…,X̂n}，还有一批从真实的分布采样而来的数据 {X1,X2,…,Xn}（也就是我们希望生成的训练集）。我们只有样本本身，没有分布表达式，当然也就没有方法算 KL 散度。

 

虽然遇到困难，但还是要想办法解决的。GAN 的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧。

就这样，WGAN 就诞生了，详细过程请参考互怼的艺术：从零直达 WGAN-GP。而 VAE 则使用了一个精致迂回的技巧。

 

VAE慢谈

对于生成模型而言，最关键的是要求出P(x)，有了P(x)，只需要sampleP较大的x，就能得到比较合理的结果图片。

首先我们有一批数据样本 {X1,…,Xn}，其整体用 X 来描述，我们本想根据 {X1,…,Xn} 得到 X 的分布 p(X)，如果能得到的话，那我直接根据 p(X) 来采样，就可以得到所有可能的 X 了（包括 {X1,…,Xn} 以外的），这是一个终极理想的生成模型了。

当然，这个理想很难实现，P(x)又取决于选用什么模型，比如后面用混合高斯模型

高斯混合，是有若干个高斯分布叠加成的，比如m个，

所以首先选中某个高斯的weight为p(m)，p(x|m)就符合该选中的高斯分布

 

于是我们将分布改一改：

这里我们就不区分求和还是求积分了，意思对了就行。此时 p(X|Z) 就描述了一个由 Z 来生成 X 的模型，而我们假设 Z 服从标准正态分布，也就是 p(Z)=N(0,I)。如果这个理想能实现，那么我们就可以先从标准正态分布中采样一个 Z，然后根据 Z 来算一个 X，也是一个很棒的生成模型。

接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下：

看出了什么问题了吗？如果像这个图的话，我们其实完全不清楚：究竟经过重新采样出来的 Zk，是不是还对应着原来的 Xk，所以我们如果直接最小化 D(X̂ k,Xk)^2（这里 D 代表某种距离函数）是很不科学的，而事实上你看代码也会发现根本不是这样实现的。

也就是说，很多教程说了一大通头头是道的话，然后写代码时却不是按照所写的文字来写，可是他们也不觉得这样会有矛盾。

VAE初现

其实，在整个 VAE 模型中，我们并没有去使用 p(Z)（先验分布）是正态分布的假设，我们用的是假设 p(Z|X)（后验分布）是正态分布

具体来说，给定一个真实样本 Xk，我们假设存在一个专属于 Xk 的分布 p(Z|Xk)（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。

为什么要强调“专属”呢？因为我们后面要训练一个生成器 X=g(Z)，希望能够把从分布 p(Z|Xk) 采样出来的一个 Zk 还原为 Xk

如果假设 p(Z) 是正态分布，然后从 p(Z) 中采样一个 Z，那么我们怎么知道这个 Z 对应于哪个真实的 X 呢？现在 p(Z|Xk) 专属于 Xk，我们有理由说从这个分布采样出来的 Z 应该要还原到 Xk 中去。

再次强调，这时候每一个 Xk 都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个 X 就有多少个正态分布了。我们知道正态分布有两组参数：均值 μ 和方差 σ^2（多元的话，它们都是向量）

那我怎么找出专属于 Xk 的正态分布 p(Z|Xk) 的均值和方差呢？好像并没有什么直接的思路。

VAE相当于一个，连续的高斯混合，即这里有无限个高斯分布选择到某个高斯分布的weight为P(z), 符合标准高斯分布z代表选中第z个高斯分布，然后P(x|z)的高斯分布的参数，mean，variance是通过nn求得

那好吧，我就用神经网络来拟合出来。这就是神经网络时代的哲学：难算的我们都用神经网络来拟合，在 WGAN 那里我们已经体验过一次了，现在再次体验到了。

于是我们构建两个神经网络 μk=f1(Xk)，logσ^2=f2(Xk) 来算它们了。我们选择拟合 logσ^2 而不是直接拟合 σ^2，是因为 σ^2 总是非负的，需要加激活函数处理，而拟合 logσ^2 不需要加激活函数，因为它可正可负。

到这里，我能知道专属于 Xk 的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个 Zk 出来，然后经过一个生成器得到 X̂k=g(Zk)。

现在我们可以放心地最小化 D(X̂k,Xk)^2，因为 Zk 是从专属 Xk 的分布中采样出来的，这个生成器应该要把开始的 Xk 还原回来。于是可以画出 VAE 的示意图：

事实上，VAE 是为每个样本构造专属的正态分布，然后采样来重构。

分布标准化

让我们来思考一下，根据上图的训练过程，最终会得到什么结果。

首先，我们希望重构 X，也就是最小化 D(X̂k,Xk)^2，但是这个重构过程受到噪声的影响，因为 Zk 是通过重新采样过的，不是直接由 encoder 算出来的。

显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。

而方差为 0 的话，也就没有随机性了，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化成普通的 AutoEncoder，噪声不再起作用。

这样不就白费力气了吗？说好的生成模型呢？

别急，其实 VAE 还让所有的 p(Z|X) 都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。

怎么理解“保证了生成能力”呢？如果所有的 p(Z|X) 都很接近标准正态分布 N(0,I)，那么根据定义：

这样我们就能达到我们的先验假设：p(Z) 是标准正态分布。然后我们就可以放心地从 N(0,I) 中采样来生成图像了。

 

 

这个前面解释过了

 

那怎么让所有的 p(Z|X)都向 N(0,I) 看齐呢？如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的 loss：

因为它们分别代表了均值 μk 和方差的对数 logσ^2，达到 N(0,I) 就是希望二者尽量接近于 0 了。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。

所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的 KL 散度 KL(N(μ,σ^2)‖N(0,I))作为这个额外的 loss，计算结果为：

这里的 d 是隐变量 Z 的维度，而 μ(i) 和 σ_{(i)}^{2} 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。直接用这个式子做补充 loss，就不用考虑均值损失和方差损失的相对比例问题了。

显然，这个 loss 也可以分两部分理解

 

推导

由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可，根据定义我们可以写出：

整个结果分为三项积分，第一项实际上就是 −logσ^2 乘以概率密度的积分（也就是 1），所以结果是 −logσ^2；第二项实际是正态分布的二阶矩，熟悉正态分布的朋友应该都清楚正态分布的二阶矩为 μ^2+σ^2；而根据定义，第三项实际上就是“-方差除以方差=-1”。所以总结果就是：

 

重参数技巧

最后是实现模型的一个技巧，英文名是 Reparameterization Trick，我这里叫它做重参数吧。

其实很简单，就是我们要从 p(Z|Xk) 中采样一个 Zk 出来，尽管我们知道了 p(Z|Xk) 是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的，于是我们利用了一个事实：

所以，我们将从 N(μ,σ^2) 采样变成了从 N(μ,σ^2) 中采样，然后通过参数变换得到从 N(μ,σ^2) 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

具体怎么实现，大家把上述文字对照着代码看一下，一下子就明白了。

 

本质是什么

VAE 的本质是什么？VAE 虽然也称是 AE（AutoEncoder）的一种，但它的做法（或者说它对网络的诠释）是别具一格的。

在 VAE 中，它的 Encoder 有两个，一个用来计算均值，一个用来计算方差，这已经让人意外了：Encoder 不是用来 Encode 的，是用来算均值和方差的，这真是大新闻了，还有均值和方差不都是统计量吗，怎么是用神经网络来算的？

事实上，我觉得 VAE 从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的。它本质上就是在我们常规的自编码器的基础上，对 encoder 的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果 decoder 能够对噪声有鲁棒性；而那个额外的 KL loss（目的是让均值为 0，方差为 1），事实上就是相当于对 encoder 的一个正则项，希望 encoder 出来的东西均有零均值。那另外一个 encoder（对应着计算方差的网络）的作用呢？它是用来动态调节噪声的强度的。直觉上来想，当 decoder 还没有训练好时（重构误差远大于 KL loss），就会适当降低噪声（KL loss 增加），使得拟合起来容易一些（重构误差开始下降）。反之，如果 decoder 训练得还不错时（重构误差小于 KL loss），这时候噪声就会增加（KL loss 减少），使得拟合更加困难了（重构误差又开始增加），这时候 decoder 就要想办法提高它的生成能力了。

说白了，重构的过程是希望没噪声的，而 KL loss 则希望有高斯噪声的，两者是对立的。所以，VAE 跟 GAN 一样，内部其实是包含了一个对抗的过程，只不过它们两者是混合起来，共同进化的。

从这个角度看，VAE 的思想似乎还高明一些，因为在 GAN 中，造假者在进化时，鉴别者是安然不动的，反之亦然。当然，这只是一个侧面，不能说明 VAE 就比 GAN 好。

GAN 真正高明的地方是：它连度量都直接训练出来了，而且这个度量往往比我们人工想的要好（然而 GAN 本身也有各种问题，这就不展开了）。

正态分布？

对于 p(Z|X) 的分布，读者可能会有疑惑：是不是必须选择正态分布？可以选择均匀分布吗？

首先，这个本身是一个实验问题，两种分布都试一下就知道了。但是从直觉上来讲，正态分布要比均匀分布更加合理，因为正态分布有两组独立的参数：均值和方差，而均匀分布只有一组。

前面我们说，在 VAE 中，重构跟噪声是相互对抗的，重构误差跟噪声强度是两个相互对抗的指标，而在改变噪声强度时原则上需要有保持均值不变的能力，不然我们很难确定重构误差增大了，究竟是均值变化了（encoder的锅）还是方差变大了（噪声的锅）。

而均匀分布不能做到保持均值不变的情况下改变方差，所以正态分布应该更加合理。

 

变分在哪里

还有一个有意思（但不大重要）的问题是：VAE 叫做“变分自编码器”，它跟变分法有什么联系？在VAE 的论文和相关解读中，好像也没看到变分法的存在？

其实如果读者已经承认了 KL 散度的话，那 VAE 好像真的跟变分没多大关系了，因为 KL 散度的定义是：

如果是离散概率分布就要写成求和，我们要证明：已概率分布 p(x)（或固定q(x)）的情况下，对于任意的概率分布 q(x)（或 p(x)），都有 KLp(x)‖q(x))≥0，而且只有当p(x)=q(x)时才等于零。

因为 KL(p(x)‖q(x))实际上是一个泛函，要对泛函求极值就要用到变分法，当然，这里的变分法只是普通微积分的平行推广，还没涉及到真正复杂的变分法。而 VAE 的变分下界，是直接基于 KL 散度就得到的。所以直接承认了 KL 散度的话，就没有变分的什么事了。

一句话，VAE 的名字中“变分”，是因为它的推导过程用到了 KL 散度及其性质。

 

VAE简短总结：为采样的真实样本中的每一个样本，构造专属的正态分布，其中的均值和方差采用神经网络进行拟合，这个专属的后验分布p(Z|Xk)是正态的，而且向标准正态分布看齐，防止随着神经网络拟合噪声（方差）慢慢趋于0（这样的话模型慢慢退化为AutoEncoder，噪声不再起作用），看齐的方式是在重构损失上加上额外的损失，即计算均值和方差的loss，从这个专属的正态分布中采样出一个Zk出来，这个Zk对应着原来的Xk，然后通过生成器得到X̂k=g(Zk)，然后最小化D(Xk, X̂k)，D是某个距离度量函数。

 

 

VAE为什么会有作用？

先看一种intuituive的解释，左边的图，对于普通的AE，如果在满月和弦月的code的中间调一个点，去做decode会得到什么?答案是不确定，因为你对code的分布并没有任何的约束而VAE引入了noise，所以对于相同的input经过encoder后虽然得到的mean和variance是相同的，但是noise是不同的，所以会有一些较小的误差如右边的图，所以对于VAE在这样的一个误差范围内的点，而不是仅仅一个点都应该能decode到满月或弦月那么对于noise区间重合的地方，就会产生渐进的图，要同时和满月或弦月都比较相似，如最右图所示

 

下图显示如何将original code转化为noise code可以看到这里的variance是学习到的，这里之所以要exp是保证variance为正

 

好，那单纯的这样去训练是不是会产生我们希望的效果？

答案是不会的，因为惰性是存在万事万物中的，能简单解决，网络也不会把自己搞的很复杂.这里如果没有任何约束，那么训练出来只要variance全为0就ok了，这样就等同于普通的AE。

所以还需要加一个约束

这个约束的红，蓝部分，如果要minimize，相减为0，这样就保证variance接近于1 (variance = exp(a))

可以看到这个约束本身就会保证有一定的noise存在，然后后面的m平方的项是，L2 regularization，正则项。

这里是前文提到的，让所有的 p(Z|X) 都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。

 

 

 

https://www.sohu.com/a/226209674_500659

https://www.zhihu.com/question/41490383/answer/103006793

https://www.bilibili.com/video/av10590361/?p=29

 

理论上formal的解释

https://www.cnblogs.com/fxjwind/p/9099931.html