R语言做单因素方差分析及其结果呈现
R语言做单因素方差分析及其结果呈现
一、数据录入
| 重复 | A | B | C |
| 1 | 85 | 80 | 55 |
| 2 | 80 | 70 | 65 |
| 3 | 91 | 75 | 49 |
| 4 | 82 | 65 | 52 |
| 5 | 90 | 60 | 60 |
| 6 | 78 | 65 | 50 |
edit()函数会自动调用一个允许手动输入数据的文本编辑器,键入数据保存即可。
data <- data.frame(A = numeric(0), B = numeric(0), C = numeric(0))
data <- edit(data)data数据集如下所示,需要进行整合。
A B C
1 85 80 55
2 80 70 65
3 91 75 49
4 82 65 52
5 90 60 60
6 78 65 50
library(reshape)
data <- melt(data,id=c())
names(data) <- c('trt', 'res') # 重命名列名整合后的数据集是这样的:
trt res
1 A 85
2 A 80
3 A 91
4 A 82
5 A 90
6 A 78
7 B 80
8 B 70
9 B 75
10 B 65
11 B 60
12 B 65
13 C 55
14 C 65
15 C 49
16 C 52
17 C 60
18 C 50
二、评估检验的假设条件
1、正态性检验
1)q-q图检验正态性假设
library(car)
qqPlot(lm(res~trt,data=data),simulate = TRUE)q-q图中,当所有点落在两条虚线之间则服从正态性,此处出现两个异常值(第7和14个值),这里不做处理。
2)shapiro.test()函数检验正态性
shapiro.test(data$res)Shapiro-Wilk normality test
data: data$res
W = 0.94544, p-value = 0.358
p值为0.358,满足正态性条件
2、方差齐性检验
bartlett.test(res ~ trt, data = data)Bartlett test of homogeneity of variances
data: res by trt
Bartlett's K-squared = 0.48205, df = 2, p-value = 0.7858
p值为0.7858,说明各组方差没有显著不同。
三、方差分析
aov <- aov(res ~ trt, data = data)
summary(aov) Df Sum Sq Mean Sq F value Pr(>F)
trt 2 2553 1276.7 31.55 4.22e-06 ***
Residuals 15 607 40.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R语言自带的分析结果中没有总和项,这里分享一个函数,添加总和项。
myaov <- function(aov){
aov <- summary(aov)
aov[[1]]["Total",] <- c(sum(aov[[1]][,1]),sum(aov[[1]][,2]),rep(NA,3))
aov}
myaov(aov)
Df Sum Sq Mean Sq F value Pr(>F)
trt 2 2553 1276.7 31.55 4.22e-06 ***
Residuals 15 607 40.5
Total 17 3160
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
四、多重比较
多重比较的方法有很多,这里用duncan检验。
library(agricolae)
duncan <- duncan.test(aov,"trt")
duncan$group res groups
A 84.33333 a
B 69.16667 b
C 55.16667 c
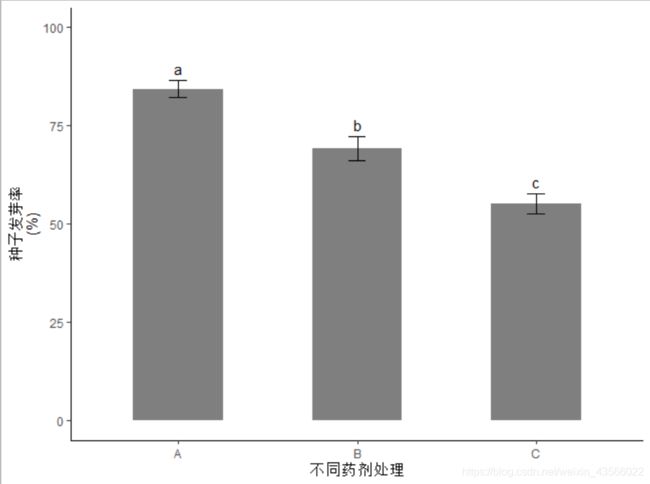
五、结果呈现
1、提取关键数据并整理
# 计算均值和标准差
mean <- aggregate(data$res, by = list(trt = data$trt), FUN = mean)
sd <- aggregate(data$res, by = list(trt = data$trt), FUN = sd)
# 计算标准误
se <- sd$x / sqrt(nrow(data) / nrow(sd))
# 合并数据
newdata <- data.frame(trt = mean$trt, mean = mean$x, sd = sd$x, se)
# 添加多重比较结果
label <- data.frame(mean = duncan$groups$res, label = duncan$groups$groups)
total <- merge(newdata, label, by = 'mean') # 合并两个数据框2、结果呈现
library(ggplot2)
p <- ggplot(total, aes(trt, mean)) + geom_bar(stat="identity",fill="grey50",width = 0.5)
# 添加误差棒
p1 <- p + geom_errorbar(aes(ymin = mean - se,ymax = mean + se), width=0.1)
# 添加显著性标志
p2 <- p1 + geom_text(aes(y = mean + se, label = label, vjust = -0.5, hjust = "center"))
# 去除网格线
p3 <- p2 + theme(panel.grid.major = element_blank(), panel.grid.minor = element_blank(), panel.background = element_blank(), axis.line = element_line(colour = "black", size = 0.6))
# 修改坐标轴标题
p4 <- p3+ labs(x = "不同药剂处理", y = "种子发芽率\n(%)")
# 修改纵坐标范围
p5 <- p4 +ylim(0,100)
p5六、拓展
1、本例采用edit()函数手动输入数据,其实这方法还是有点繁琐的,建议直接用R语言读取文本文件、EXCEL等。
2、本文使用了一些整理数据的函数。reshape包是一套重构和整合数据集的绝妙的万能工具,事实上,R语言在整理数据方面有诸多优点,如整合、重构、筛选、排序、合并数据等。
3、方差分析最容易忽视的一点是没有对方差分析的检验条件进行评估,拿一个不符合条件的数据去做方差分析,显然是不合适的,其结果的可靠性容易遭受质疑。
4、本例数据本应先进行数据变换再进行方差分析,以下分享几点关于数据变换的建议:
1)对数变换
适用条件:属于大范围变动的正整数资料,不符合泊松分布,平均数与方差呈正相关或平均数与标准差成正比
转换方式:当资料没有零,且大多数值大于0时,x’=log10(x)
当资料的值多数小于0,且有0存在,x’=log10(x+1)
2)平方根变换
适用条件:往往符合泊松分布,方差与平均数相等、方差与平均数成正比,或方差与非可加效应成正比;二项变量以百分比表示的资料,如果处于0~30%之间或70%~100%之间,但并非两种情况并存时,前者可将%前的数据看做X,后者则要以100为被减数,其差数作为X,进行平方根变换。
转换方式:当大多数大于10时,x=sqrt(x)
当多数小于10,且有0存在,x=sqrt(x+1)
3)反正弦平方根变换
适用条件:符合二项分布,以百分比或小数表示的资料,当百分比值范围很大时,如跨及三段范围(0~30%,30%~70%,70~100%)时,采用反正弦变换
转换方式:x=asin(sqrt(x)), x为小数。