R语言_方差分析

方差分析与回归分析

在回归分析中，通过量化的预测变量来预测量化的响应变量，建立了相应的回归模型。
同时，预测变量也不一定是量化的，还可以是名义型或者有序型变量。这种情况下，关注的重点通常在组间的差异性分析，称为方差分析（ANOVA）。

术语

单因素组间方差分析

这里，观测数相同，称为均衡设计，若不同称为非均衡设计。
方差显著性通过F检定来检定。

单因素组内方差分析

单因素组内方差分析，又叫做重复测量方差分析。

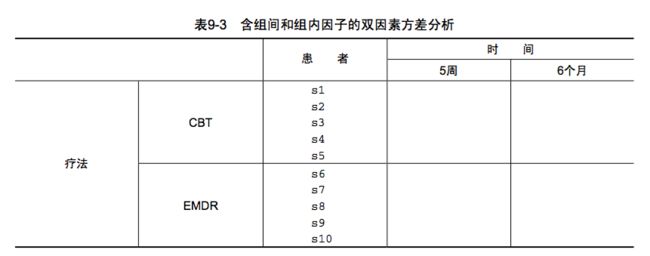
含组间和组内因子的双因素方差分析

含有疗法和时间两个因子时，既可以分析疗法的影响（时间跨度上的平均），也可以分析时间的影响（疗法类型跨度上的平均），还可以分析疗法与时间的交互影响。
前两个称之为主效应，后两个称之为交互效应。

当设计包含两个或者更多因子时，便是因素方差设计，比如两因子时称作双因素方差分析，三因子时称为三因素方差分析。若因子设计中包含组内和组件因子，又称为混合模型方差分析。
上图例子为典型的双因素混合模型方差分析。

本例中，需要做三次F检定。主效应两次，交互效应一次。
若疗法效果显著，说明CBT和EMDR对焦虑症的治疗效果不同。
若时间结果显著，说明焦虑度从五周到六个月发生了变化。
若两者交互效应显著，说明：（1）焦虑症从周五到周六的改变程度在两种疗法中是不同的。（2）焦虑症在CBT和EMDR中得效果程度在时间跨度上是不同的。

协方差分析

上面分析了疗法和时间两个因素对焦虑症的影响，属于双因素混合模型方差分析。

有一个问题需要考虑：治疗后的差异可能是由于治疗前情况的差异产生。即：抑郁症对病症有影响，且抑郁症和焦虑症经常同时出现。
抑郁症也可以解释因变量的组件差异，因此被称为混淆变量（confounding factor）。如果对抑郁症不感兴趣，被称为干扰变数（nuisance variable）。

如果事先知道患者的抑郁症水平（BDI），那么就可以在评测疗法类型的影响前，对任何抑郁水平的组间差异进行调整。
本案例中，BDI为协变量，该设计分析为协方差分析（ANCOVA）。

多元方差分析

以上，因变量只有一个（STAI），为增强结果的有效性，可以对焦虑症进行其他测量（家庭评分，医生评分，对日常行为的影响评价）。
当因变量不只有一个，设计被称为多元方差分析(MANOVA)。

多元协方差分析

多元方差分析中，如果协变量也存在，就叫做多元协方差分析。

总结

ANOVA 方差分析
ANCOVA 协方差分析
MANOVA 多元方差分析

ANOVA模型拟合

ANOVA和回归方法，都是广义线性模型的特例。

aov函数

表达式中各项顺序

越基础的效应更应该放在前面。
协变量——主效应——双因素的交互项——三因素的交互项。

单因素方差分析

单因素方差分析，感兴趣的是：针对该单因素的不同组别的因变量，均值是否存在显著差异。

一个例子

library(multcomp)
attach(cholesterol)
table(trt)
aggregate(response,by=list(trt),FUN=mean)
aggregate(response,by=list(trt),FUN=sd)
fit = aov(response~trt)
summary(fit)
library(gplots)
plotmeans(response~trt,
          xlab="treatment",ylab="response",
          main = "mean plot\nwith 95% CI")
boxplot(response~trt)

多重比较

上面例子的ANOVA对各个疗法的F检验表明了五种药物疗法效果不同，但并未指出哪种疗法与其他不同。
多重比较可以解决这个问题。

#删除存在兼容性的包HH
detach("package::HH")
TukeyHSD(fit)
opar = par(no.readonly=TRUE)
par(las=2)
par(mar=c(5,8,4,2))
plot(TukeyHSD(fit)) #置信区间包含0说明差异不显著
#另一种多重比较展现
#有相同字母的组说明均值差异不显著
library(multcomp)
par(opar)
par(mar=c(5,4,6,2))
tuk = glht(fit,linfct=mcp(trt="Tukey"))
plot(cld(tuk,level=.05),col="lightgrey")

评估检验的假设条件

统计中，我们对检验结果的信心程度依赖于检验的数据是否满足条件的假设。

单因素方差分析中，假设因变量服从正态分布，各组方差相等。

正态假设

#正态检验
library(car)
qqPlot(lm(response~trt,data=cholesterol),
       simulate=T, main="Q-Q plot",
       labels = F)
#数据落在95%置信区间，说明满足正态假设

方差齐性假设

#方差齐性检验
bartlett.test(response~trt,data=cholesterol)
#方差检验，表明五组方差并没有显著不同

离群点检测

#离群点
#方差齐性分析对离群点非常敏感
library(car)
outlier.test(fit)

单因素协方差分析

一个例子

detach(cholesterol)
#自变量是怀孕小鼠不同剂量的药物处理，因变量是剩下幼崽的体重均值
#协变量是怀孕时间
data(litter,package="multcomp")
attach(litter)
table(dose)
table(gesttime)
aggregate(weight,by=list(dose),mean)
aggregate(weight,by=list(dose,gesttime),mean)
fit = aov(weight~gesttime+dose)
summary(fit)
#ANCOVA表明
#（1）怀孕时间与幼崽的出生体重有关
#（2）控制怀孕时间，药物剂量与幼崽的出生体重有关
#去除协变量效应后的组均值
library(effects)
effect("dose",fit)

多重比较

#用户定义的对照的多重比较
#假设：未用药与其他三种用药影响不同
library(multcomp)
contrast = rbind("no drug vs. drug" = c(3,-1,-1,-1))
class(contrast)
summary(glht(fit,linfct=mcp(dose=contrast)))
#p值小，表明0.05水平下影响不同

评估检验假设条件

ANCOVA和ANOVA一样，都需要正态性还有方差齐性的假设。
此外，ANCOVA还假设回归斜率相同。

在这个问题中，回归斜率相同指的是：四个处理组中，通过怀孕时间预测出生体重的回归斜率相同。
ANCOVA模型包含的怀孕时间*剂量的交互项，可对回归斜率的同质性进行检验。交互效应如果显著，表明时间和幼崽出生体重间的关系依赖于药物剂量的水平。

#检验回归斜率的同质性
library(multcomp)
fit2 = aov(weight~gesttime*dose,data=litter)
summary(fit2)
#可以看到，交互效益不显著，支持了斜率相等的假设。
#如果显著，可以尝试变换协变量与因变量

可视化

HH包中的ancova()可以绘制因变量、协变量、因子之间的关系。

detach("multcomp")
library(HH)
ancova(weight~gesttime+dose,data=litter)

双因素方差分析

#自变量为“喂食方法”*“抗坏血酸含量”
#因变量为牙齿长度
attach(ToothGrowth)
table(supp,dose) #均衡设计,不用担心顺序问题
aggregate(len,by=list(supp,dose),mean)
aggregate(len,by=list(supp,dose),sd)
fit = aov(len~supp*dose)
summary(fit)

#可视化
#(1)
interaction.plot(dose,supp,len,type="b",
                 col=c("red","blue"),pch=c(16,18),
                 main = "interaction between dose and supplement type")
#(2)
library(HH)
interaction2wt(len~supp*dose)

重复测量方差分析

多元方差分析

用回归来做ANOVA