Python计算机视觉第六章 图像聚类
文章目录
- 引言
- 6.1K-means聚类
-
- 6.1.1Scipy聚类包
- 6.1.2图像聚类
- 6.1.3在主成分上可视化图像
- 6.1.4像素聚类
- 6.2层次聚类
- 6.3谱聚类
引言
本章将介绍几种聚类方法,并展示如何利用它们对图像进行聚类,从而寻找相似的
图像组。聚类可以用于识别、划分图像数据集,组织与导航。此外,我们还会对聚
类后的图像进行相似性可视化。
6.1K-means聚类
K-means 是一种将输入数据划分成 k 个簇的简单的聚类算法。K-means反复提炼初始评估的类中心,步骤如下:
1.以随机或猜测的方式初始化类中心ui,i=1…k;
2.将每个数据点归并到离他距离最近的类中心所属的类ci;
3.对所有属于该类的数据点求平均,将平均值作为新的类中心;
4.重复步骤(2)和步骤(3)直到收敛。
K-means试图使类内总方差最小;
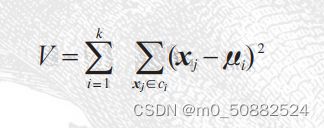
避免初始化类中心时没选取好类中心初值所造成的结果,该算法通常会初始化不同的类中心进行多次运算,然后选择方差V最小的结果。下面分析优缺点。
缺陷:必须预先设定聚类数k,选择不恰当则会导致聚类出来的结果很差。
优点:容易实现,可以并行计算,并且对于很多别的问题不需要任何调整就能够直接使用。
6.1.1Scipy聚类包
尽管 K-means 算法很容易实现,但我们没有必要自己实现它。SciPy 矢量量化包
scipy.cluster.vq 中有 K-means 的实现,下面是使用方法。
from pylab import *
from scipy.cluster.vq import *
#生成简单二维数据
class1 = 1.5 * randn(100, 2)
class2 = randn(100, 2) + array([5, 5])
features = vstack((class1, class2))
#用k=2对数据进行聚类
centroids, variance = kmeans(features, 2)
#用矢量量化函数对每个数据点进行归类:
code, distance = vq(features, centroids)
#可视化,画出这些数据点及最终的聚类中心 函数where()给出每个类的索引
figure()
ndx = where(code == 0)[0]
plot(features[ndx, 0], features[ndx, 1], '*')
ndx = where(code == 1)[0]
plot(features[ndx, 0], features[ndx, 1], 'r.')
plot(centroids[:, 0], centroids[:, 1], 'go')
axis('off')
show()

类中心标记为绿色大圆环,预测出的类分别标记为蓝色星号和红色点。
6.1.2图像聚类
用K-means对文字图像进行聚类。由于在网上没有找到所需的字体数据集,本节及下一节代码及实验引入了其他博主的实验
import imtools
import pickle
from pylab import *
from scipy.cluster.vq import *
from PIL import Image
# 获取 selectedfontimages 文件下图像文件名,并保存在列表中
imlist = imtools.get_imlist('selectedfontimages/a_selected_thumbs')
imnbr = len(imlist)
# 载入模型文件
with open('fontimages/font_pca_modes.pkl','rb') as f:
immean = pickle.load(f)
V = pickle.load(f)
# 创建矩阵,存储所有拉成一组形式后的图像
immatrix = array([array(Image.open(im)).flatten()
for im in imlist],'f')
# 投影到前 40 个主成分上
immean = immean.flatten()
projected = array([dot(V[:40],immatrix[i]-immean) for i in range(imnbr)])
# 进行 k-means 聚类
projected = whiten(projected)
centroids,distortion = kmeans(projected,4)
code,distance = vq(projected,centroids)
# 绘制聚类簇
for k in range(4):
ind = where(code==k)[0]
figure()
gray()
for i in range(minimum(len(ind),40)):
subplot(4,10,i+1)
imshow(immatrix[ind[i]].reshape((25,25)))
axis('off')
show()
6.1.3在主成分上可视化图像
为了便于观察上面是如何利用主成分进行聚类的,我们可以在一对主成分方向的坐
标上可视化这些图像。
设定聚类数k=4,并进行归一化,可视化聚类后的结果为:
# -*- coding: utf-8 -*-
import imtools, pca
from PIL import Image, ImageDraw
from pylab import *
imlist = imtools.get_imlist('selectedfontimages/a_selected_thumbs')
imnbr = len(imlist)
# Load images, run PCA.
immatrix = array([array(Image.open(im)).flatten() for im in imlist], 'f')
V, S, immean = pca.pca(immatrix)
# Project on 2 PCs.
projected = array([dot(V[[0, 1]], immatrix[i] - immean) for i in range(imnbr)]) # P131 Fig6-3左图
#projected = array([dot(V[[1, 2]], immatrix[i] - immean) for i in range(imnbr)]) # P131 Fig6-3右图
# height and width
h, w = 1200, 1200
# create a new image with a white background
img = Image.new('RGB', (w, h), (255, 255, 255))
draw = ImageDraw.Draw(img)
# draw axis
draw.line((0, h/2, w, h/2), fill=(255, 0, 0))
draw.line((w/2, 0, w/2, h), fill=(255, 0, 0))
# scale coordinates to fit
scale = abs(projected).max(0)
scaled = floor(array([(p/scale) * (w/2 - 20, h/2 - 20) + (w/2, h/2)
for p in projected])).astype(int)
# paste thumbnail of each image
for i in range(imnbr):
nodeim = Image.open(imlist[i])
nodeim.thumbnail((25, 25))
ns = nodeim.size
box = (scaled[i][0] - ns[0] // 2, scaled[i][1] - ns[1] // 2,
scaled[i][0] + ns[0] // 2 + 1, scaled[i][1] + ns[1] // 2 + 1)
img.paste(nodeim, box)
img.show()
img.save('pca_font.png')
6.1.4像素聚类
在结束本节之前,我们来看一个对单幅图像中的像素而非全部图像进行聚类的例子。
将图像区域或像素合并成有意义的部分称为图像分割,它是第 9 章的主题。
单纯在像素水平上应用 K-means 得出的结果往往是毫无意义的。要产生有意义的结果,往往需要更复杂的类模型而非平均像素色彩或空间一致性。现在,我们仅会在 RGB 三通道的像素值上运用 K-means 进行聚类,
from scipy.cluster.vq import *
#from scipy.misc import imresize
from pylab import *
from PIL import Image
# 添加中文字体支持
def scipy_misc_imresize(arr, size, interp='bilinear', mode=None):
im = Image.fromarray(arr, mode=mode)
ts = type(size)
if np.issubdtype(ts, np.signedinteger):
percent = size / 100.0
size = tuple((np.array(im.size)*percent).astype(int))
elif np.issubdtype(type(size), np.floating):
size = tuple((np.array(im.size)*size).astype(int))
else:
size = (size[1], size[0])
func = {'nearest': 0, 'lanczos': 1, 'bilinear': 2, 'bicubic': 3, 'cubic': 3}
imnew = im.resize(size, resample=func[interp]) # 调用PIL库中的resize函数
return np.array(imnew)
steps = 50 # image is divided in steps*steps region
infile = '17.jpg'
im = array(Image.open(infile))
dx = im.shape[0] / steps
dy = im.shape[1] / steps
# compute color features for each region
features = []
for x in range(steps):
for y in range(steps):
R = mean(im[int(x * dx):int((x + 1) * dx), int(y * dy):int((y + 1) * dy), 0])
G = mean(im[int(x * dx):int((x + 1) * dx), int(y * dy):int((y + 1) * dy), 1])
B = mean(im[int(x * dx):int((x + 1) * dx), int(y * dy):int((y + 1) * dy), 2])
features.append([R, G, B])
features = array(features, 'f') # make into array
# cluster
centroids, variance = kmeans(features, 3)
code, distance = vq(features, centroids)
# create image with cluster labels
codeim = code.reshape(steps, steps)
codeim = scipy_misc_imresize(codeim, im.shape[:2], 'nearest')
figure()
ax1 = subplot(121)
#ax1.set_title('Image')
axis('off')
imshow(im)
ax2 = subplot(122)
#ax2.set_title('Image after clustering')
axis('off')
gray()
imshow(codeim)
show()


第二组图像某些区域没有空间一致性,从实验结果中可以看出很难将它们分开,如灯柱,杂乱的树木等。
6.2层次聚类
层次聚类(或凝聚式聚类)是另一种简单但有效的聚类算法,其思想是基于样本间
成对距离建立一个简相似性树。该算法首先将特征向量距离最近的两个样本归并为
一组,并在树中创建一个“平均”节点,将这两个距离最近的样本作为该“平均”
节点下的子节点;然后在剩下的包含任意平均节点的样本中寻找下一个最近的对,
重复进行前面的操作。在每一个节点处保存了两个子节点之间的距离。遍历整个树,
通过设定的阈值,遍历过程可以在比阈值大的节点位置终止,从而提取出聚类簇。
层次聚类由若干优点,例如,利用树结构可以可视化数据间的关系,并显示这些簇是如何关联的。在树中,一个好的特征向量可以给出一个很好的分离结果。另外一个优点是,对于给定的不同的阈值,可以直接利用原来的树,而不需要重新计算。不足之处是,对于实际需要的聚类簇,我们需要选择一个合适的阈值。
from itertools import combinations
from pylab import *
class ClusterNode(object):
def __init__(self,vec,left,right,distance=0.0,count=1):
self.left = left
self.right = right
self.vec = vec
self.distance = distance
self.count = count
def extract_clusters(self, dist):
"""从层次聚类树中提取距离小于dist的子树簇群列表"""
if self.distance < dist:
return [self]
return self.left.extract_clusters(dist) + self.right.extract_clusters(dist)
def get_cluster_elements(self):
"""在聚类子树中返回元素的id"""
return self.left.get_cluster_elements() + self.right.get_cluster_elements()
def get_height(self):
"""返回节点的高度,高度是各分支的和"""
return self.left.get_height() + self.right.get_height()
def get_depth(self):
"""返回节点的深度,深度是每个子节点取最大再加上它的自身距离"""
return max(self.left.get_depth(), self.right.get_depth()) + self.distance
class ClusterLeafNode(object):
def __init__(self,vec,id):
self.vec = vec
self.id = id
def extract_clusters(self, dist):
return [self]
def get_cluster_elements(self):
return [self.id]
def get_height(self):
return 1
def get_depth(self):
return 0
def L2dist(v1,v2):
return sqrt(sum((v1-v2)**2))
def L1dist(v1,v2):
return sum(abs(v1-v2))
def hcluster(features,distfcn=L2dist):
"""用层次聚类对行特征进行聚类"""
# 用于保存计算出的距离
distances = {}
# 每行初始化为一个簇
node = [(ClusterLeafNode(array(f), id=i) for i, f in enumerate(features))]
while len(node) > 1:
closet = float('Inf')
# 遍历每对,寻找最小距离
for ni, nj in combinations(node, 2):
if (ni, nj) not in distances:
distances[ni, nj] = distfcn(ni.vec, nj.vec)
d = distances[ni, nj]
if d < closet:
closet = d
lowestpair = (ni, nj)
ni, nj = lowestpair
# 对两个簇求平均
new_vec = (ni.vec + nj.vec) / 2.0
# 创建新的节点
new_node = ClusterNode(new_vec, left=ni, right=nj, distance=closet)
node.remove(ni)
node.remove(nj)
node.append(new_node)
return node[0]
我们为树节点创建了两个类,即ClusterNode和ClusterLeafNode,这两个类将用于创建聚类树,其中函数hcluster()用于创建树。首先创建一个包含叶节点的列表,然后根据选择的距离度量方式将距离最近的对归并到一起,返回的终节点即为树的根。对于一个行为特征向量的矩阵,运行hcluster()会创建和返回聚类树。
距离度量的选择依赖于实际的特征向量,利用欧式距离L2(同时提供了L1距离度量函数),可以创建任意距离度量函数,并将它作为参数传递给hcluster()。对于每个子树,计算其所有节点特征向量的平均值,作为新的特征向量来表示该子树,并将每个子树视为一个对象。当然,还有其他将哪两个节点合并在一起的方案,比如在两个子树中使用对象间距离最小的单向锁,及在两个子树中用对象间距离最大的完全锁。选择不同的锁会生成不同类型的聚类树。
为了从树中提取聚类簇,需要从顶部遍历树直至一个距离小于设定阈值的节点终止,这通过递归很容易做到。ClusterNode的extract_clusters()方法用于处理该过程,如果节点间距离小于阈值,则用一个列表返回节点,否则调用子节点(叶节点通常返回他们自身)。调用该函数会返回一个包含聚类簇的子树列表。对于每一个子聚类簇,为了得到包含对象id的叶节点,需要遍历每个字数,并用方法get_cluster_elements()返回一个包含叶节点的列表。
6.3谱聚类
谱聚类方法是一种有趣的聚类算法,与前面 K-means 和层次聚类方法截然不同。
对于 n 个元素(如 n 幅图像),相似矩阵(或亲和矩阵,有时也称距离矩阵)是一个
n×n 的矩阵,矩阵每个元素表示两两之间的相似性分数。谱聚类是由相似性矩阵构
建谱矩阵而得名的。对该谱矩阵进行特征分解得到的特征向量可以用于降维,然后
聚类。
谱聚类的优点之一是仅需输入相似性矩阵,并且可以采用你所想到的任意度量方式构建该相似性矩阵。像K-means和层次聚类需要计算那些特征向量求平均;为了计算平均值,会将特征或描述子限制为向量。而对于谱方法,特征向量就没有类别限制,只要有一个“距离”或“相似性”的概念即可。
下面说明谱聚类的过程。给定一个n×n的相似矩阵S,sij为相似性分数,我们可以创建一个矩阵,称为拉普拉斯矩阵:
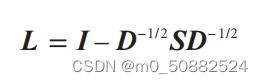
其中,I 是单位矩阵,D 是对角矩阵,对角线上的元素是 S 对应行元素之和,
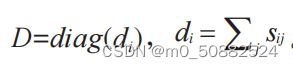
拉普拉斯矩阵中D为
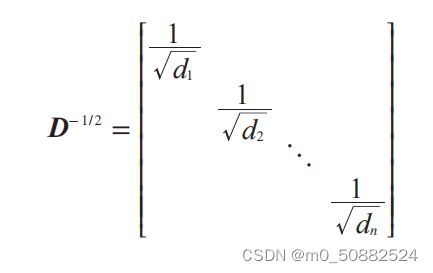
为了简洁表示,使用较小的值并且要求sij⩾0。
计算L的特征向量,并使用k个最大特征值对应的k个特征向量,构建出一个特征向量集,从而可以找到聚类簇。创建一个矩阵,该矩阵的各列是由之前求出的k个特征向量构成,每一行可以看作一个新的特征向量,长度为k。本质上,谱聚类算法是将原始空间中的数据转换成更容易聚类的新特征向量。在某些情况下,不会首先使用聚类算法。
# -*- coding: utf-8 -*-
from PCV.tools import imtools, pca
from PIL import Image, ImageDraw
from pylab import *
from scipy.cluster.vq import *
imlist = imtools.get_imlist('D:\\Python\\chapter6\\selectedfontimages\\a_selected_thumbs')
imnbr = len(imlist)
# Load images, run PCA.
immatrix = array([array(Image.open(im)).flatten() for im in imlist], 'f')
V, S, immean = pca.pca(immatrix)
# Project on 2 PCs.
projected = array([dot(V[[0, 1]], immatrix[i] - immean) for i in range(imnbr)]) # P131 Fig6-3左图
# projected = array([dot(V[[1, 2]], immatrix[i] - immean) for i in range(imnbr)]) # P131 Fig6-3右图
n = len(projected)
# 计算距离矩阵
S = array([[sqrt(sum((projected[i] - projected[j]) ** 2))
for i in range(n)] for j in range(n)], 'f')
# 创建拉普拉斯矩阵
rowsum = sum(S, axis=0)
D = diag(1 / sqrt(rowsum))
I = identity(n)
L = I - dot(D, dot(S, D))
# 计算矩阵 L 的特征向量
U, sigma, V = linalg.svd(L)
k = 5
# 从矩阵 L 的前k个特征向量(eigenvector)中创建特征向量(feature vector) # 叠加特征向量作为数组的列
features = array(V[:k]).T
# k-means 聚类
features = whiten(features)
centroids, distortion = kmeans(features, k)
code, distance = vq(features, centroids)
# 绘制聚类簇
for c in range(k):
ind = where(code == c)[0]
figure()
gray()
for i in range(minimum(len(ind), 39)):
im = Image.open(imlist[ind[i]])
subplot(4, 10, i + 1)
imshow(array(im))
axis('equal')
axis('off')
show()