具有平滑正曲线边界的一般凸体的精确闭式闵可夫斯基研究（Matlab代码实现）

 ‍个人主页：研学社的博客 

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 Matlab代码实现

4 参考文献

---

1 概述

欧几里得空间的闭式参数公式，边界是平滑的，并且每个点都有正截面曲率。在这些条件下，每个边界点的位置与表面法线之间存在唯一的关系。

主要结果表示为两个定理：

• 定理 1（文章中的定理 4.1）：使用每个表面点的单位法向量直接参数化闵可夫斯基和。虽然在数学上表达起来很简单，但这种参数化并不总是实用的计算方式;
• 定理 2（文章中的定理 4.3）：使用未归一化的梯度推导出一个更有用的参数闭式表达式。

在两个椭球体的特殊情况下，建议的表达式与以前使用几何解释导出的表达式相同。为了检验结果，对两个超二次体之间的闵可夫斯基和进行了数值验证和比较。

讨论并演示了两种应用：

• 在运动规划问题中产生配置空间障碍;
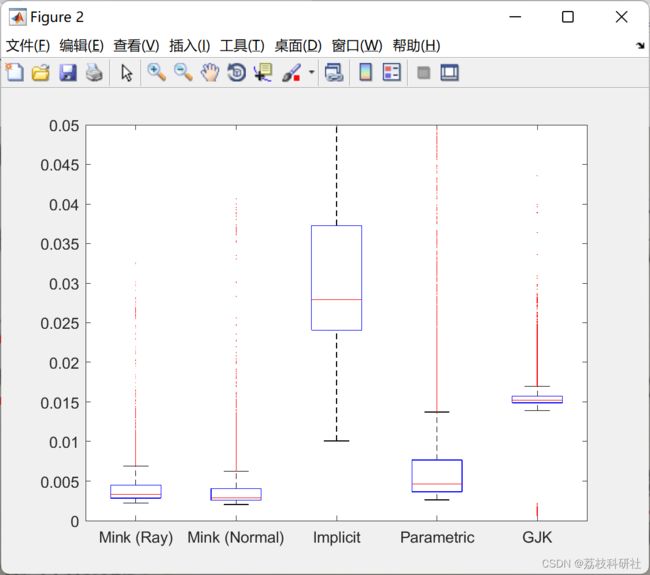
• 提高基于优化的碰撞检测算法的性能。

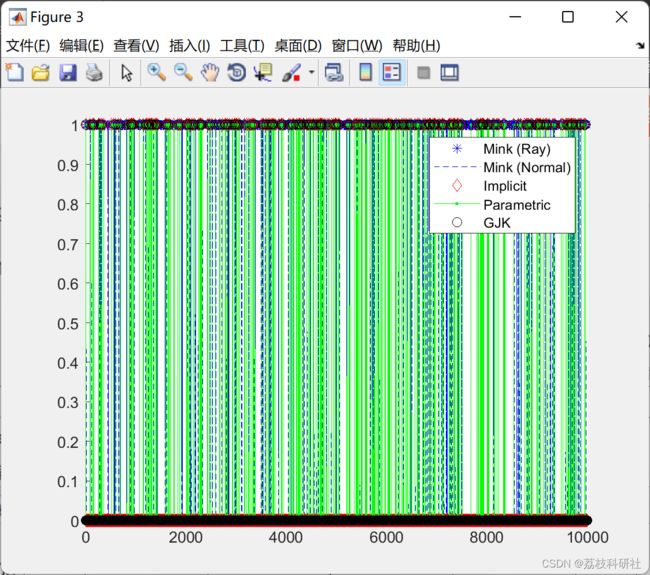
2 运行结果

  

  

  

  

  

这里仅展现部分运行结果。 

部分代码：

close all; clear; clc;

add_paths();

% Robot
N_vtx = 50;
robot = SuperEllipse([5*rand, 3*rand, rand, 0, 0, 0, pi*rand, N_vtx]);
robot_config = [robot.a, robot.eps, robot.tc', robot.ang];

% Generate environment
N = [1,10,50,200,500,1e3,5e3,1e4];
% N = [1,10,50,200,500];
N_ang = 50;
c_obs = cell(1,length(N));
obstacle = cell(1,length(N));
obs_config = cell(1,length(N));

run_time = zeros(1,length(N));

%% Main routine
disp('****************************************************************')
disp('Application on configuration-space obstacle generations in SE(2)')
disp('****************************************************************')
for i = 1:length(N)
    disp(['Number of obstacles: ', num2str(N(i))])
    
    [obstacle{i}, obs_config{i}] = generate_obstacle(N(i));
    
    % Minkowski sums
    mink = cell(N(i), N_ang);
    ti = tic;
    for k = 1:N_ang
        robot_ang = (k-1)*pi/N_ang;
        for j = 1:N(i)
            minkObj = MinkSumClosedForm(robot, obstacle{i}{j},...
                rot2(robot_ang), rot2(obstacle{i}{j}.ang));
            m1 = robot.GetGradients();
            mink{j,k} = minkObj.GetMinkSumFromGradient(m1) +...
                obstacle{i}{j}.tc;
        end
    end
    run_time(i) = toc(ti);
    
    c_obs{i} = mink;
end

%% Plots
figure; hold on; grid on; axis off;
idx = 5;
bd = 220;

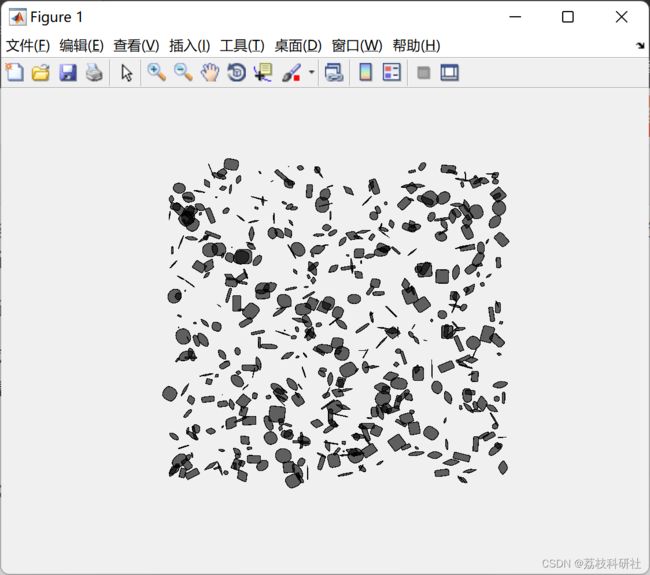
for i = 1:N(idx)
    % obstacles in workspace
    obstacle = SuperEllipse([obs_config{idx}(i,1:3), 0,...
        obs_config{idx}(i,4:end), N_vtx]);
    obstacle.PlotShape('k');
end

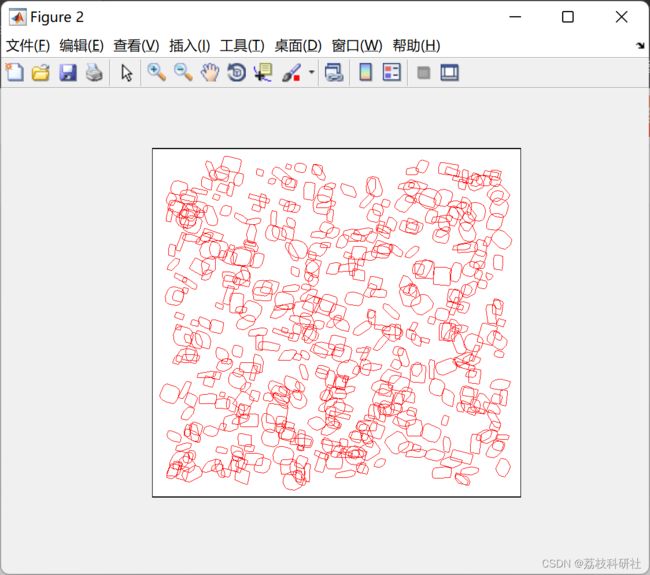
figure; hold on; grid on; axis off;
for i = 1:N(idx)
    % obstacles in workspace
    obstacle = SuperEllipse([obs_config{idx}(i,1:3), 0,...
        obs_config{idx}(i,4:end), N_vtx]);
    obstacle.PlotShape('k');
    
    for k = 1:5:N_ang
        % c-obstacles
        robot_ang = (k-1)*pi/N_ang;
        plot3(c_obs{idx}{i,k}(1,:), c_obs{idx}{i,k}(2,:),...
            robot_ang*ones(1,50), 'r-', 'LineWidth', 0.1)
        
        % arena boundary
        arena = [[-bd;-bd;robot_ang], [-bd;bd;robot_ang],...
            [bd;bd;robot_ang], [bd;-bd;robot_ang]];
        patch(arena(1,:), arena(2,:), arena(3,:), 'w')
    end
end

xlabel('x')
ylabel('y')
zlabel('\theta')

figure; hold on;
plot(N, run_time);

%% Subroutine for generate N random obstacles
function [obstacle, obs_config] = generate_obstacle(N)
obs_a = 10*rand(2,N);
obs_eps = 2 * rand(1,N);
obs_taper = zeros(1,N);
obs_tx = 200 * (2*rand(2,N)-1);
obs_th = pi * rand(1,N);

obstacle = cell(1,N);
for i = 1:N
    obstacle{i} = SuperEllipse([obs_a(:,i)', obs_eps(i), obs_taper(i),...
        obs_tx(1,i), obs_tx(2,i), obs_th(i), 50]);
end

obs_config = [obs_a; obs_eps; obs_tx; obs_th]';
end

3 Matlab代码实现

4 参考文献

部分理论来源于网络，如有侵权请联系删除。

 [1]Ruan, S. and Chirikjian, G.S., 2021. Closed-Form Minkowski Sums of Convex Bodies with Smooth Positively Curved Boundaries. Computer-Aided Design, p.103133.