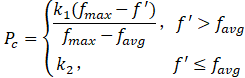智能优化算法：遗传算法（GA）

 目录

目录

1.遗传算法原理介绍及其算子选择

2.算法步骤 

3.案例分析

4. 代码实现

---

---

1.遗传算法原理介绍及其算子选择

        遗传算法（Genetic Algorithm，GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。

        用遗传算法解决TSP问题时，染色体对应每条可行路径，基因对应经过的城市顺序，交叉变异即对经过的城市顺序进行交叉或变异操作，产生一个新的可行解，再计算其适应度，令优秀个体拥有更大的交叉机会，如此往复，直至达到结束条件。

        编码方式主要有二进制编码和实数编码两种方式，在本题中若将解直接编码为二进制，例如如果有6个城市，则编码为30个二进制，这种编码不能直接判断约束条件，而且会产生很多不可行解，大大增加了算法的难度和浪费了大量资源。所以在本题中采取实数编码的方式，实数编码可以直接在解的表现型上进行遗传操作，大大提高了算法的搜索效率。对每个城市进行编号，基因即为所经城市编号，而染色体为所经城市的编号集，并且确保每个城市只出现一次。

        适应度是评判个体优劣的标准，并且作为遗传操作的唯一依据，所以适应度函数的选择尤为重要。个体适应度越高，被选择的概率就越高，反之就低。在本题中需计算遍历各个城市的最短路径，因此个体的所经城市路径总长度即可作为该个体的适应度值，但是在选择时优先选择的为适应度值高的个体，但在本题中个体越优秀其距离越短，即适应度值越低，所以需要对其进行变换，使其适应度值与个体优劣程度成正比。分析可得此问题为最小化问题，则令其距离的倒数为该个体适应度值。其适应度函数如下（公式(1)）：

(1)

        选择操作也称为复制操作，是从当前群体中按照一定概率选出优良个体，使他们有机会作为父代繁殖下一代子孙。在遗传算法中哪个个体被选择是按照一定概率进行的，适应度值越大被选择的概率就越大，但并不代表一定会被选上。同样，适应度值低的个体被选择的概率就低，但也可能会被选上。为了使个体被选择的概率和其适应度值成比例，本题决定采用适应度比例方法（又称蒙特卡洛法）计算个体被选择的概率。假设种群规模为M，个体i的适应度值为fi，则其被选择的概率为：

(2)

        个体选择方法采用轮盘赌，即按照个体的选择概率产生一个轮盘，轮盘每个区的角度与个体的选择概率成正比，随机产生一个数，它落入轮盘的哪个区域就选择相应的个体。在实际操作中可以按照个体顺序计算每个个体的累计概率，则随机数落入累计概率的哪个区域就选择相应的个体。

        交叉是指两个个体配对或复制时，他们的染色体相互混合，产生一对由双方基因组成的新的染色体。交叉后得到的子代继承了父代的基因，优良基因会使得子代更加优秀，在后续的选择中被保留，而不良基因可能会导致子代被淘汰，因此产生的子代总是比父代生存和复制的更好。遗传算法通过交叉算子维持种群的多样性，一个好的交叉算子能够保证种群丰富的多样性，更利于产生优秀个体，因此交叉算子的选择是遗传算法的核心部分。经过分析发现部分匹配交叉法（PMX）在处理TSP问题时拥有好的性能，能够快速的完成交叉过程并且很好的保留父代优秀基因，更利于产生优秀个体。

        部分匹配交叉法在进行交叉操作时，首先需要选择两个交叉点（两条染色体交叉点相同），然后交叉两组基因，最后进行冲突检测，根据交换的两组基因建立映射关系，将发生冲突的基因进行转换，确保每条染色体中基因不重复，即每个城市只出现一次，如图3所示。

        变异算子选取替换变异方法（DM），其性能优于IVM、ISM等算法。替换变异操作是在父代个体中选择一个子位串，然后再随机在剩下的位串中选择一个点位，并插入该子位串，如图4所示

2.算法步骤 

遗传算法步骤如下：

Step 1：随机产生一个含有M个染色体的初始种群 pop(1)，t:=1；

Step 2：对群体 pop(t) 中的诶条染色体 popi(t) ，计算它的适应度值：fi=fitness[popi(t)]；

Step 3：若满足停止条件则结束，否则以概率为依据选择父代染色体；

Step 4：以概率 Pc 对选择的父代染色体进行交叉操作，得到一个新的群体 crosspop(t+1)；

Step 5：以概率 Pm 对 crosspop(t+1)中的染色体进行变异操作，形成 mutpopt+1；t≔t+1，得到新的种群 pop(t)= mutpopt+1；返回Step 2。

        种群规模会影响遗传优化的结果和效率，若种群规模太小，优化性能将会降低，容易陷入局部最优解，种群规模太大则会增加计算复杂度。种群规模一般取20-100，但具体数量还需根据实验决定。

        交叉概率 Pc 决定所选父代染色体是否进行交叉操作，随机产生一个概率，若小于 Pc 则进行交叉，否则不交叉。若 Pc 过高则可能破坏优良基因，若过低则会使搜索陷入迟钝状态。实验表明通常Pc∈[0.25,1.00]且取值在0.7左右最为理想。同样，变异概率 Pm 决定染色体是否进行变异操作，通常 Pm 不宜过大，防止群体中的优秀基因丢失，实验表明 Pm 通常取0.001左右。

        本题采用自适应的遗传算法，其 Pc （公式（3））和 Pm（公式（4））分别按照下列公式自动进行调整，其中k1、k2、k3、k4均为（0,1）之间的常数，fmax为群体中最大的适应度值，favg为每代群体的平均适应度值，f' 为交叉的两个个体中较大的适应度值，f 为变异个体的适应度值。

(3)

(4)

3.案例分析

        重庆，作为巴渝文化的发源地，“8D魔幻城市”，近年来持续占据网红城市排行榜前列。重庆不仅拥有众多的土著美食，还有独具特色的自然风光。为了给游客提供合理的旅行攻略，现假设游客周游重庆26个区、8个县、4个自治县，最后回到出发点，每个地区仅经过一次。请以旅行距离最短和旅行时间最短分别设计两份旅行攻略供该游客参考。

        旅行方式分为飞机（900 km/h），动车(250km/h)，汽车(80km/h)，根据重庆市实际的机场，火车站分布情况，建立旅行时间最短的数学模型，并使用智能算法求解模型，获取旅行时间最短的行程攻略。

经过不断地迭代测试，得到了以下数据：

表3 迭代次数不变改变种群数量最短距离

次数 规模	1	2	3	4	5	6	平均值
50	2072.131	2010.591	2114.047	2188.307	1939.449	2071.695	2066.036667
80	1849.802	1868.683	1891.334	1869.744	1906.603	1901.914	1881.346667
100	2086.859	1905.036	1759.982	1945.847	1878.433	1845.208	1903.560833
200	1925.144	1860.170	1845.099	1952.308	1807.812	1791.759	1863.715333
500	1844.224	1777.235	1845.257	1763.626	1850.922	1908.812	1831.679333
1000	1762.259	1875.643	1900.193	1951.808	1759.520	1851.889	1850.218667

*迭代次数为5000次，单位：km

        通过分析数据发现迭代次数不变时随着种群规模的不断增大，越来越容易得到路径总长度更小的解，但是当种群规模达到一定程度时所得到的的最优解范围变小，趋于平稳，并且种群规模越大其迭代的所需的算力资源和运行时间也随之增加。所以通过数据综合分析得到种群规模在500左右时最佳，最容易得到最优解。

表4 种群数量不变改变迭代次数最短距离

次数 迭代次数	1	2	3	4	5	6	平均值
100	1830.670	1866.702	1873.367	1990.074	2199.522	2073.702	1972.3395
500	1913.824	1967.240	1911.471	1798.132	1876.723	1955.368	1903.793
1000	2008.671	1880.881	1878.420	1896.768	1949.271	1912.334	1921.0575
2000	1894.796	1934.509	1872.972	1773.676	1886.818	1907.958	1878.454833
5000	1845.384	1819.245	1835.075	1846.870	1752.388	1872.893	1828.6425
10000	1806.961	1829.342	1840.172	1715.395	1869.046	1789.991	1808.4845
20000	1828.322	1844.982	1831.445	1877.161	1820.853	1862.321	1844.180667

*种群数量为500，单位：km

        通过实验得到表4和图5，经过分析发现随着迭代次数的增加，越来越容易得到较优解，但当迭代次数超出一定范围后其种群适应度值趋于稳定，即种群达到收敛，即使再次增加迭代次数也难以产生适应度值更高的个体，并且在种群收敛后再增加迭代次数此时的算法就变成了普通的遍历搜索。通过图5可以直观看出在迭代超过4000次后种群便很难再产生适应度值更高的个体，即表明在迭代4000次后种群已经基本收敛。所以通过综合表4与图5数据可以得出最佳迭代次数应在5000次左右。

        综上所述，根据实验结果分析，该自适应遗传算法的最佳种群规模为500，最佳迭代次数为5000次左右。设置该参数为实验参数，通过多次迭代得到历代最优解变化图，如图6。

        通过大量实验表明，该算法得到的有效最优解一般在1800公里左右，在本次100次迭代实验中最优解平均值为1805.503383公里，最大值为1868.6825664公里，最小值为1722.4851023公里。即通过遗传算法可以得到从北碚出发游历重庆并回到北碚的最短距离为1722.4851023公里，其具体路径如下：

北碚区→沙坪坝区→大渡口区→九龙坡区→南岸区→渝中区→江北区→渝北区→长寿区→涪陵区→丰都县→垫江县→梁平县→万州区→云阳县→奉节县→巫山县→巫溪县→城口县→开州区→忠县→石柱土家族自治县→黔江区→酉阳土家族苗族自治县→秀山土家族苗族自治县→彭水苗族土家族自治县→武隆县→南川区→綦江区→巴南区→江津区→永川区→荣昌县→大足区→璧山区→铜梁区→潼南县→合川区→北碚区

4. 代码实现

        代码比较乱，但是能用，代码里面我刚开始有限制出发点必须是北碚区，但是后面发现最后只要是闭环起始点是哪个都一样，但是好像改不回去了，我记得改之前好像是跑出来过几百公里的数据的但是改之后基本都是一两千，大家可以尝试改一下，由该回来的友友麻烦告诉我一声。代码在运行的时候不是特别稳定，因为有时候会陷入局部最优解，可能交叉变异之后就没有与要求符合的基因了，代码可能就会卡在那里，解决办法就只能调整迭代次数，或者重新运行，看运气，运气好就不会卡住。这个代码是可以计算最短距离和最短时间的，只需要把距离矩阵改成时间矩阵就可以了，如果不知道在哪里该可以私信或者留言。注意事项就这么多了，总之就是代码比较乱，逻辑没问题，至于结果怎么样以及怎么优化就看各位了，哈哈哈哈，我不想再搞了。

        读取数据是读的Excel，工具是jxl，数据的具体格式看下面那个图片。依次就是名称，经度，纬度，是否有飞机场，是否有火车站，有的话就是1，没有就是0。

 

4.1 基因类

package TSPga;

import java.util.*;

public class Chromosome implements Cloneable{
	 private int[] tour;
	 private double[][] distance;//距离矩阵
	 private int cityNum;//城市数量
	 private double fitness;//适应度值，即每条线路路程

	 public Chromosome(){
	     cityNum = 20;
	     tour = new int[cityNum];
	     distance = new double[cityNum][cityNum];
	  }
	 public Chromosome(int num, double[][] distance){
	     this.cityNum = num;
	     tour = new int[cityNum];
	     this.distance = distance;
	   }
	 //随机产生一条染色体，即随机产生一条路径
	 public void randomGeneration(){
		 //创建Vector类型数组存储城市
	     Vector allowedCities = new Vector();
	     for (int i = 1; i < cityNum; i++) {
	      allowedCities.add(Integer.valueOf(i));//将指定的元素添加到此向量的末尾
	     }//产生顺序序列：allowedCities=[0,1,2,3,4......]
	     //Random r = new Random(System.currentTimeMillis());//随机数产生，返回当前计算机时间
	     Random r = new Random();
	     tour[0] = 0;
	     for (int i = 1; i < cityNum; i++) {
	    	int index = r.nextInt(allowedCities.size());//在[0，allowedCities.size()）之间取随机整数
	        int selectedCity = allowedCities.get(index).intValue();//返回向量中index位置的元素并取其整数部分
	        tour[i] = selectedCity;//存储随机产生路径
	        allowedCities.remove(index);//移除向量中与index匹配的第一个元素项，即将以及用过的城市除去
	      }
	     
	     }
	    
	 public void print(){
	    for (int i = 0; i < cityNum; i++) {
	      System.out.print(tour[i] + ",");
	    }
	    
	    System.out.println();//System.out.println(tour.length);
	    System.out.println("Its fitness measure is: "+ getFitness());
	 }
	 
	 //计算适应度，即总距离
	 private double calculatefitness(){
	     double fitness = 0.0;
	     double len = 0;
	      for (int i = 0; i < cityNum - 1; i++) {
	          len += distance[this.tour[i]][this.tour[i+1]]; //计算每条染色体（路径）的总距离
	      }
	     len += distance[this.tour[0]][this.tour[cityNum-1]];//加上最后一个城市回到出发点距离，形成闭环
	     
	      fitness = 1.0/len;//距离越短，fitness越大
	     return fitness;
	    }
	    
	   public int[] getTour() {
	      return tour;
	    }
	  
	    public void setTour(int[] tour) {
	      this.tour = tour;
	    }
	  
	  public double[][] getDistance() {
	     return distance;
	   }
	  
     public void setDistance(double[][] distance) {
	   this.distance = distance;
	   }
	
	   public int getCityNum() {
	      return cityNum;
	  }
	 
	   public void setCityNum(int cityNum) {
	     this.cityNum = cityNum;
	   }
	  
	   public double getFitness() {
	      this.fitness = calculatefitness();
	      return fitness;
	   }
	  
	    public void setFitness(double fitness) {
	      this.fitness = fitness;
	    }
	  
	   @Override
	  protected Object clone() throws CloneNotSupportedException {
		   
		   Chromosome chromosome = (Chromosome) super.clone();
		   chromosome.cityNum = this.cityNum;
		   chromosome.distance = this.distance.clone();
		   chromosome.tour = this.tour.clone();
		   chromosome.fitness = this.fitness;
		   return chromosome;
	   }

}

4.2 交叉变异类

package TSPga;

import java.io.*;
import java .util.*;
import jxl.NumberCell;
import jxl.Sheet;
import jxl.Workbook;
import jxl.read.biff.BiffException;

public class GA {
	private static final double R = 6371.004;
	private Chromosome[] chromosomes;
	private Chromosome[] chromosomes1;
	private Chromosome[] nextGeneration;
	private int N;//种群数量
	private int cityNum;//城市数量
	private double Pc;//交叉概率
	private double Pm;//变异概率
	private int MAX_GEN;//迭代次数
	private double bestLength;
	private int[] bestTour;
	private double bestFitness;
	private double[] BestFitness;
	private double[] averageFitness;
	private double[][] distance;//距离矩阵
	private double[][] time;//时间矩阵
	double[] xx;//用来输出最佳路径每个城市位置
	double[] yy;//用来输出最佳路径每个城市位置
	private String filename;
	private int[] plane;//存储是否有机场
	private int[] railway;//是否有铁路
	
	public GA(int n, int num, int g, double p_c, double p_m, String filename) {
		this.N = n;
		this.cityNum = num;
		this.MAX_GEN = g;
		this.Pc = p_c;
		this.Pm = p_m;
		bestTour = new int [cityNum];
		averageFitness = new double[MAX_GEN];
		BestFitness = new double[MAX_GEN];
		bestFitness = 0.0;
		chromosomes = new Chromosome[N];
		chromosomes1 = new Chromosome[N/2];
		nextGeneration = new Chromosome[N];
		distance = new double[cityNum][cityNum];
		time = new double[cityNum][cityNum];
		xx = new double[cityNum];
		yy = new double[cityNum];
		plane = new int[cityNum];
		railway = new int[cityNum];
		this.filename = filename;
	}
	
	public void solve() throws BiffException, IOException, CloneNotSupportedException{
		System.out.println("---------------------Start initilization---------------------");
		init();//产生染色体，种群，以及计算距离矩阵和适应度√
		System.out.println("---------------------End initilization---------------------");
		System.out.println("---------------------Start evolution---------------------");
		for (int i = 0; i < MAX_GEN; i++) {
			System.out.println("-----------Start generation "+ i+"----------");
			evolve(i);
			System.out.println("-----------End generation "+ i+"----------");
		}
		System.out.println("---------------------End evolution---------------------");
		printOptimal();
		outputResults();
		
		double sum=0;
		for(int i=0;i selectionP[k] && p <= selectionP[k+1]) {
							selectedCity = k;
						}
						if (k==0 && random.nextDouble() <= selectionP[k]) {
							selectedCity = 0;
						}
					}
						
					a++;
					try {
						if(chromosomes[selectedCity].getFitness() >= averageFitness[g]) {
							children[j] = (Chromosome) chromosomes[selectedCity].clone();
							//System.out.println("cj:"+chromosomes[selectedCity].getFitness());
							//System.out.println("avg:"+averageFitness[g]);
							FLAG=false;
							//break;
						}
						else if(a != 99){
							FLAG=true;
						}
						else {
							children[j] = (Chromosome) chromosomes[selectedCity].clone();
							FLAG=false;
						}
					}
					catch(CloneNotSupportedException e){
						e.printStackTrace();
					}
				
				}
			}
		//for(int i = 0;i < N;i = i + 2) {
			//System.out.println("11111");
			//交叉操作(PMX)
			//System.out.println("----------Start crossover----------");
			//System.out.println();
			//Random random = new Random(System.currentTimeMillis());
			boolean flag = true;
			while(flag){
				flag = false;
			if (random.nextDouble() < Pc) {
				//System.out.println("crossover");
				//random = new Random(System.currentTimeMillis());
				//定义两个cut点
				int cutPoint1 = -1;
				int cutPoint2 = -1;
				//选择交叉点
				boolean FLAG=true;//确保 0 0 && r1 < cityNum -1) {
							cutPoint1 = r1;
							x1=cutPoint1;
							//random = new Random(System.currentTimeMillis());
							int r2 = random.nextInt(cityNum - r1);
							if (r2 == 0) {
								cutPoint2 = r1 + 1;
								x2=cutPoint2;
							}
							else if(r2 > 0){
								cutPoint2 = r1 + r2;
								x2=cutPoint2;
							}
							FLAG = false;
						}
						else
							FLAG = true;
					}
						if(x2 - x1 <= 38) {
							FLAG1 = false;
						}
						else {
							FLAG1 = true;
						}	
						
				}
					 /*System.out.println("The two tours are: ");
					 for (int j = 0; j < cityNum; j++) {
						 System.out.print(tour1[j] +"\t");
					}
						 System.out.println();
						 for (int j = 0; j < cityNum; j++) {
						 System.out.print(tour2[j] +"\t");
						 }
						 System.out.println();*/
					 for (int j = 0; j < cityNum; j++) {
						 if (j >= cutPoint1 && j <= cutPoint2) {
							int tmp1 = children[0].getTour()[j];
							 children[0].getTour()[j] = children[1].getTour()[j];
							 children[1].getTour()[j] = tmp1;
						 }
					 }
					 
					 int [] tour1 = new int[cityNum];
					 int [] tour2 = new int[cityNum];
					 for(int i1=0;i1 0 && r1 < cityNum -1) {
						cutPoint1 = r1;
						//random = new Random(System.currentTimeMillis());
						int r2 = random.nextInt(cityNum - r1);
						if (r2 == 0) {
							cutPoint2 = r1 + 1;
						}
						else if(r2 > 0){
						    cutPoint2 = r1 + r2;
						}
					}
					if (cutPoint1 > 0 && cutPoint2 > 0) {
						 List tour = new ArrayList();
						 //System.out.println("Cut point1 is "+cutPoint1+", and cut point2 is "+cutPoint2);
						 if (cutPoint2 == cityNum - 1) {
							 for (int k = 0; k < cutPoint1; k++) {
								 tour.add(Integer.valueOf(children[j].getTour()[k]));
							 }
						 }
						 else {
							 for (int k = 0; k < cityNum; k++) {
								 if (k < cutPoint1 || k > cutPoint2) {
									 tour.add(Integer.valueOf(children[j].getTour()[k]));
								 }
							 }
						 }
						 //random = new Random(System.currentTimeMillis());
						 int position = random.nextInt(tour.size());
						 if (position == 0) {
							 for (int k = cutPoint2; k >= cutPoint1; k--) {
								 tour.add(0, Integer.valueOf(children[j].getTour()[k]));//在第0个位置插入值
							 }
						 }
						 else if(position == tour.size()-1){
							 for (int k = cutPoint1; k <= cutPoint2; k++) {
								 tour.add(Integer.valueOf(children[j].getTour()[k]));
							 }
						 }
						 else {
							 for (int k = cutPoint1; k <= cutPoint2; k++) {
								 tour.add(position, Integer.valueOf(children[j].getTour()[k]));
							 }
						 }
						 
						 for (int k = 0; k < cityNum; k++) {
							 children[j].getTour()[k] = tour.get(k).intValue();
						 }
					}
				}
			}
			if(children[0].getTour()[0] !=0 || children[0].getTour()[0] !=0) {
				flag1 = true;
			}
		}
			nextGeneration[i] = children[0];
			nextGeneration[i+1] = children[1];
		}
		
		//当种群中重复个体大于一定值时引入新个体
		int[] a=new int[N];
		int b=0;
		for(int i=0;i=x){
				Chromosome chromosome = new Chromosome(cityNum, distance);
				for(int a1=0;a1

 4.3 主类

package TSPga;

import java.io.IOException;
import jxl.read.biff.BiffException;

public class GAmain {
	public static void main(String[] args) throws  BiffException, IOException, CloneNotSupportedException {
		//依次输入种群规模，城市数量，迭代次数，交叉率，变异率，文件路径
		GA ga = new GA(500, 38, 5000, 0.8, 0.02, "tspga.xls");
		ga.solve();
	}
}