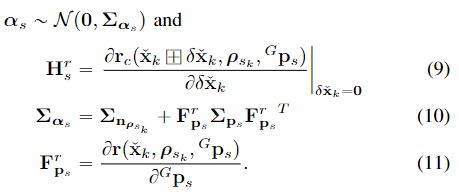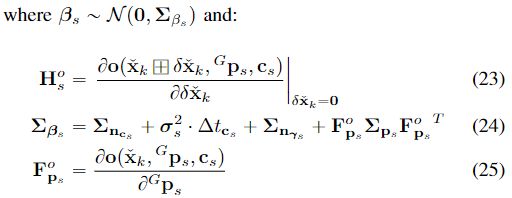R3LIVE代码详解(四)
0. 简介
上一节中,我们过完了VIO中的状态预测以及特征点跟踪部分。此时我们已经拿到了光流的特征点信息,而这部分越来越接近我们想要去讲的帧到帧的VIO部分了。这一节,我们将围绕着VIO部分来进行讲解
1. PNP误差更新
我们从之前的博客《经典文献阅读之–R3LIVE》了解到,帧到帧的VIO是将三维地图点投影到上一个图像帧获取二维座标然后通过LK光流法获取到在当前帧的二维坐标,然后可以通过ESIKF计算误差更新状态(计算PNP,更新ESIKF)
而ESIKF更新VIO是通过最小化PNP误差更新的,对应了下面这部分代码
// Pnp求解,然后更新img_pose
if ( op_track.remove_outlier_using_ransac_pnp( img_pose ) == 0 )
{
cout << ANSI_COLOR_RED_BOLD << "****** Remove_outlier_using_ransac_pnp error*****" << ANSI_COLOR_RESET << endl;
}
我们知道PnP(Perspective-n-Point)是求解3D到2D点的对应方法。它描述了当知道n个3D空间点及其位置,如何估计相机的位姿。详细推导看上面链接即可,这里就不过多展开了。
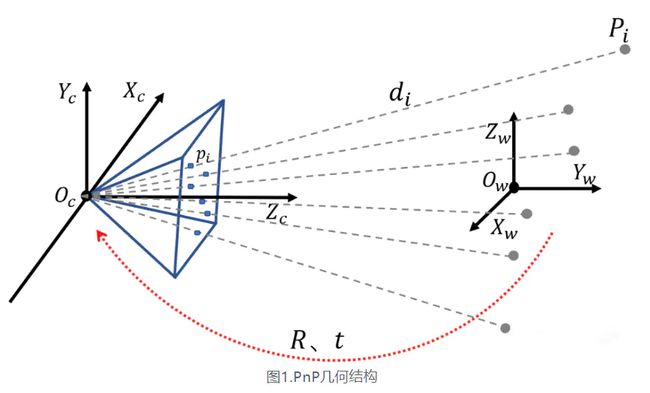
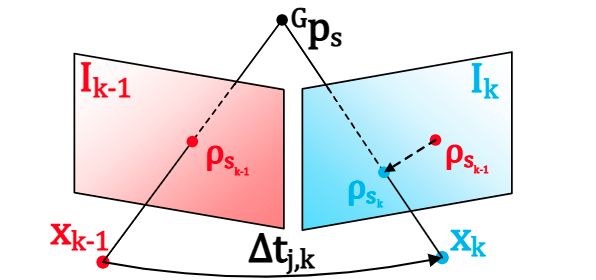
对于帧间追踪,假设上一帧追踪到 m m m个地图点 P = { P 1 , … , P m } \mathcal{P}=\left\{\mathbf{P}_{1}, \ldots, \mathbf{P}_{m}\right\} P={P1,…,Pm},它们在上一帧图像平面上的投影点也是知道的,通过LK光流可以得到这些投影点在当前帧上的估计位置。随后构建重投影误差,通过ESIKF的方式更新状态 x k {\mathbf{x}}_{k} xk。下面我们来看一下代码中PNP是如何求出误差的:
if ( 1 )
{
std::vector< int > status;
try
{
cv::solvePnPRansac( pt_3d_vec, pt_2d_vec, m_intrinsic, cv::Mat(), r_vec, t_vec, false, 200, 1.5, 0.99,
status ); // SOLVEPNP_ITERATIVE
}
catch ( cv::Exception &e )
{
scope_color( ANSI_COLOR_RED_BOLD );
cout << "Catching a cv exception: " << e.msg << endl;
return 0;
}
if ( if_remove_ourlier )
{
// Remove outlier
m_map_rgb_pts_in_last_frame_pos.clear();
m_map_rgb_pts_in_current_frame_pos.clear();
for ( unsigned int i = 0; i < status.size(); i++ )
{
int inlier_idx = status[ i ];
{
m_map_rgb_pts_in_last_frame_pos[ map_ptr_vec[ inlier_idx ] ] = pt_2d_vec[ inlier_idx ];
m_map_rgb_pts_in_current_frame_pos[ map_ptr_vec[ inlier_idx ] ] = pt_2d_vec[ inlier_idx ];
}
}
}
update_last_tracking_vector_and_ids();
}
文中的公式3,4代表了投影误差计算,公式3中 C p s ^Cp_s Cps代表了在相机坐标系下的 s s s点。 I k − 1 I_{k-1} Ik−1代表了上一时刻的图像帧,以及他们在 I k − 1 \mathbf{I}_{k-1} Ik−1中会存在有 { ρ 1 k , … , ρ m k } \left\{\mathcal{\rho}_{1_k}, \ldots, \mathcal{\rho}_{m_k}\right\} {ρ1k,…,ρmk},投影误差对应了公式4。
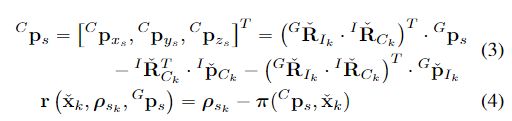
其中公式4中的 π ( C p s , x ˇ k ) ∈ R 2 \pi(^Cp_s,\check{x}_k)\in\mathbb{R}^2 π(Cps,xˇk)∈R2项是公式5,其中第一项是针孔相机模型的投影函数,第二项为在线时间校正因子(Online-temporal correction factor)。

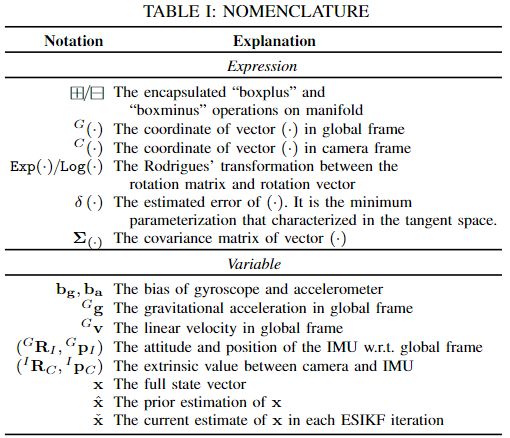
相关的符号具体含义可以参考下面的表格
2. 帧到帧VIO
下面就是完成帧到帧的VIO的部分了
///vio_esikf,依据重投影误差,更新优化状态量state_out
res_esikf = vio_esikf( state_out, op_track );
g_cost_time_logger.record( tim, "Vio_f2f" );
tim.tic( "Vio_f2m" );
对应的函数为vio_esikf文中提到,测量噪声包含两个来源,一个是像素追踪误差,另一个是地图点定位误差:
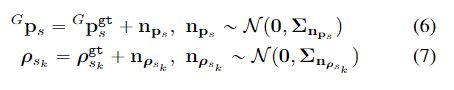
其中 G p s g t ^G\mathbf{p}_{s}^{\mathrm{gt}} Gpsgt和 ρ s k g t \rho_{s_{k}}^{\mathrm{gt}} ρskgt分别为 G p s ^G\mathbf{p}_{s} Gps和 ρ s k \rho_{s_{k}} ρsk的真值。然后根据公式4将残差一阶泰勒展开
![]()
// 遍历当前帧跟踪到的地图点
for ( auto it = op_track.m_map_rgb_pts_in_last_frame_pos.begin(); it != op_track.m_map_rgb_pts_in_last_frame_pos.end(); it++ )
{
// 取地图坐标系中的地图点坐标
pt_3d_w = ( ( RGB_pts * ) it->first )->get_pos();
// 跟踪像素点的速度
pt_img_vel = ( ( RGB_pts * ) it->first )->m_img_vel;
// 该地图点对应于上一帧的像素点坐标
pt_img_measure = vec_2( it->second.x, it->second.y );
// 将地图点从世界坐标系变换到当前帧相机坐标系
pt_3d_cam = R_w2c * pt_3d_w + t_w2c;
// 利用相机模型以及估计的相机-imu时间偏差导致的增量,得到地图点在当前帧图像的投影像素坐标 pt_img_proj
pt_img_proj = vec_2( fx * pt_3d_cam( 0 ) / pt_3d_cam( 2 ) + cx, fy * pt_3d_cam( 1 ) / pt_3d_cam( 2 ) + cy ) + time_td * pt_img_vel;
// 计算重投影误差,这里计算的是误差的大小,不用于迭代求解,只是用来确定huber核函数
double repro_err = ( pt_img_proj - pt_img_measure ).norm();
double huber_loss_scale = get_huber_loss_scale( repro_err );//huber 1.0
pt_idx++;
acc_reprojection_error += repro_err;
// if (iter_count == 0 || ((repro_err - last_reprojection_error_vec[pt_idx]) < 1.5))
if ( iter_count == 0 || ( ( repro_err - last_avr_repro_err * 5.0 ) < 0 ) )
{
last_reprojection_error_vec[ pt_idx ] = repro_err;
}
else
{
last_reprojection_error_vec[ pt_idx ] = repro_err;
}
avail_pt_count++;
根据这个一阶展开,可以和IMU传播的先验分布组合,获得当前估计位姿的MAP
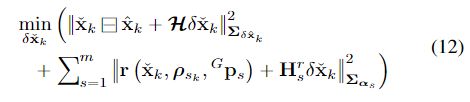
其中 ∥ x ∥ ∑ 2 = x T ∑ − 1 x \|x\|^2_{\sum}=x^T\sum^{-1}x ∥x∥∑2=xT∑−1x是带有协方差 ∑ \sum ∑的马氏距离平方, x ^ k \hat{x}_k x^k是IMU传播的状态估计, H \mathcal{H} H是从 x ^ k \hat{x}_k x^k切平面投影到 x ˇ k \check{x}_k xˇk切平面的状态误差的雅克比矩阵,其中公式(12)的详细推导可以看R2LIVE的E小节。
// Appendix E of r2live_Supplementary_material.
// https://github.com/hku-mars/r2live/blob/master/supply/r2live_Supplementary_material.pdf
// 像素对相机点求雅可比
mat_pre << fx / pt_3d_cam( 2 ), 0, -fx * pt_3d_cam( 0 ) / pt_3d_cam( 2 ), 0, fy / pt_3d_cam( 2 ), -fy * pt_3d_cam( 1 ) / pt_3d_cam( 2 );
pt_hat = Sophus::SO3d::hat( ( R_imu.transpose() * ( pt_3d_w - t_imu ) ) );//IMU系下地图点 p(IMU)^ = R(IMU <-- W) * ( p(W) - p(IMU) )
mat_A = state_iter.rot_ext_i2c.transpose() * pt_hat;//3 * 3, R(C <-- IMU) * p(imu)^
mat_B = -state_iter.rot_ext_i2c.transpose() * ( R_imu.transpose() );// - R(C <--IMU) * R(IMU <-- W)
mat_C = Sophus::SO3d::hat( pt_3d_cam );// p(C)^
mat_D = -state_iter.rot_ext_i2c.transpose();// - R(C <-- IMU)
meas_vec.block( pt_idx * 2, 0, 2, 1 ) = ( pt_img_proj - pt_img_measure ) * huber_loss_scale / img_res_scale;//观测向量填充
H_mat.block( pt_idx * 2, 0, 2, 3 ) = mat_pre * mat_A * huber_loss_scale;// H, 1-2行,前3列, 对R(IMU)雅可比
H_mat.block( pt_idx * 2, 3, 2, 3 ) = mat_pre * mat_B * huber_loss_scale;// H, 1-2行,4-6列,对P(IMU)雅可比
if ( DIM_OF_STATES > 24 )
{
// Estimate time td. 对时间差的导数
H_mat.block( pt_idx * 2, 24, 2, 1 ) = pt_img_vel * huber_loss_scale;// H,1-2行, 25-26列,对像素速度雅可比
// H_mat(pt_idx * 2, 24) = pt_img_vel(0) * huber_loss_scale;
// H_mat(pt_idx * 2 + 1, 24) = pt_img_vel(1) * huber_loss_scale;
}
if ( m_if_estimate_i2c_extrinsic )
{
H_mat.block( pt_idx * 2, 18, 2, 3 ) = mat_pre * mat_C * huber_loss_scale;//H ,1-2行,19-21列,对外参R(IMU<--C)雅可比
H_mat.block( pt_idx * 2, 21, 2, 3 ) = mat_pre * mat_D * huber_loss_scale;//H ,1-2行,22-24列,对外参t(IMU<--C)雅可比
}
if ( m_if_estimate_intrinsic )
{
H_mat( pt_idx * 2, 25 ) = pt_3d_cam( 0 ) / pt_3d_cam( 2 ) * huber_loss_scale;//H,1行,26列,对内参fx雅可比
H_mat( pt_idx * 2 + 1, 26 ) = pt_3d_cam( 1 ) / pt_3d_cam( 2 ) * huber_loss_scale;//H,2行,27列,对内参fy雅可比
H_mat( pt_idx * 2, 27 ) = 1 * huber_loss_scale;//H,1行,28列,对内参cx雅可比
H_mat( pt_idx * 2 + 1, 28 ) = 1 * huber_loss_scale;//H,2行,29列,对内参cy雅可比
}
}
给出卡尔曼滤波的相关定义:
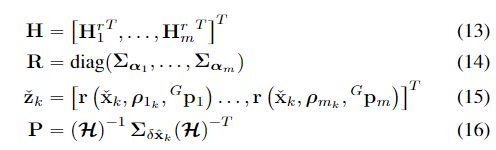
卡尔曼增益可以定义为:
![]()
状态更新为:
![]()
并且根据FAST-LIO2的公式推导,这样的迭代更新过程是等价于高斯牛顿优化的,对应的代码如下。
H_mat = H_mat / img_res_scale;
acc_reprojection_error /= total_pt_size;
last_avr_repro_err = acc_reprojection_error;
if ( avail_pt_count < minimum_iteration_pts )
{
break;
}
H_mat_spa = H_mat.sparseView();
Eigen::SparseMatrix< double > Hsub_T_temp_mat = H_mat_spa.transpose();
vec_spa = ( state_iter - state_in ).sparseView();
H_T_H_spa = Hsub_T_temp_mat * H_mat_spa;
// Notice that we have combine some matrix using () in order to boost the matrix multiplication.
//(H^T * H + P^-1)^-1
Eigen::SparseMatrix< double > temp_inv_mat =
( ( H_T_H_spa.toDense() + eigen_mat< -1, -1 >( state_in.cov * m_cam_measurement_weight ).inverse() ).inverse() ).sparseView();
KH_spa = temp_inv_mat * ( Hsub_T_temp_mat * H_mat_spa );//K * H
// (H^T * H + P^-1)^-1 * ( H^T * (-Z) ) - ( I - K * H) * (X_k - X_0)
// delta_error_X = X_k+1 - X_k = -K * Z - (I - K * H) * (X_k - X_0)
solution = ( temp_inv_mat * ( Hsub_T_temp_mat * ( ( -1 * meas_vec.sparseView() ) ) ) - ( I_STATE_spa - KH_spa ) * vec_spa ).toDense();
state_iter = state_iter + solution;
if ( fabs( acc_reprojection_error - last_repro_err ) < 0.01 )
{
break;
}
last_repro_err = acc_reprojection_error;
3. 帧到地图VIO
帧到地图的光度误差更新,这部分代码在帧与帧VIO后,基本上和帧到帧的VIO一样。
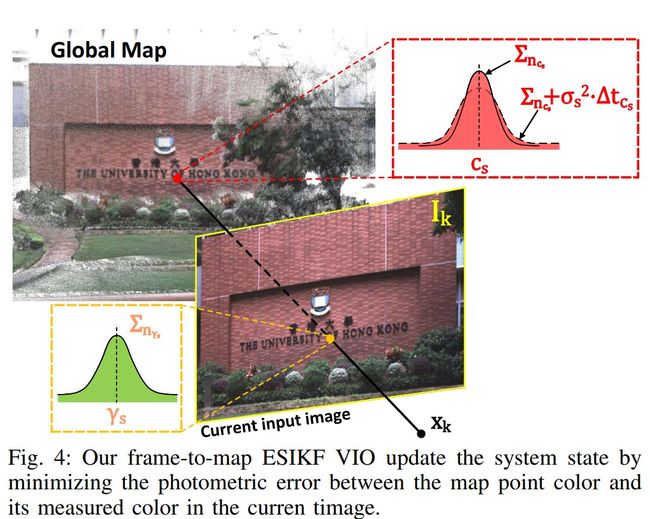
在帧间VIO更新后,我们得到了一个更新好的估计状态 x ˇ k \check{x}_k xˇk,然后我们通过最小跟踪点的光度误差来求解帧到地图,以降低漂移。
///以ESIKF形式,依据rgb误差,更新优化状态量state_out
res_photometric = vio_photometric( state_out, op_track, img_pose );
g_cost_time_logger.record( tim, "Vio_f2m" );
g_lio_state = state_out;//更新当前body的状态量
print_dash_board();
set_image_pose( img_pose, state_out );//更新image状态量
误差直接用帧到三维地图点的光度误差,公式如下,其中 c s c_s cs是保存在全局地图中点的颜色, γ s \gamma_s γs是当前帧图像 I k \mathbf{I}_k Ik中观测到的颜色。
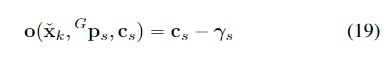
为了获得观测颜色以及协方差矩阵 ∑ n γ s \sum_{n_{\gamma_s}} ∑nγs,文中预测当前帧图像 I k \mathbf{I}_k Ik上的点坐标 ρ ~ s k = π ( C p s , x ˇ k ) \tilde{\rho}_{s_k}= \pi(^Cp_s,\check{x}_k) ρ~sk=π(Cps,xˇk),然后线性差值计算得到相邻像素的RGB颜色。同时两个参数有各自对应的测量噪声。
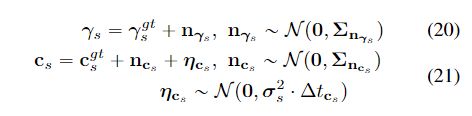
与前面一样,根据前面的19-21,完成一阶泰勒展开:
![]()
///遍历所有地图点,计算雅可比矩阵和观测向量
for ( auto it = op_track.m_map_rgb_pts_in_last_frame_pos.begin(); it != op_track.m_map_rgb_pts_in_last_frame_pos.end(); it++ )
{
if ( ( ( RGB_pts * ) it->first )->m_N_rgb < 3 ) //没有rgb跳过
{
continue;
}
pt_idx++;
pt_3d_w = ( ( RGB_pts * ) it->first )->get_pos();
pt_img_vel = ( ( RGB_pts * ) it->first )->m_img_vel;
pt_img_measure = vec_2( it->second.x, it->second.y );
pt_3d_cam = R_w2c * pt_3d_w + t_w2c; //3D地图点转换到相机系下
pt_img_proj = vec_2( fx * pt_3d_cam( 0 ) / pt_3d_cam( 2 ) + cx, fy * pt_3d_cam( 1 ) / pt_3d_cam( 2 ) + cy ) + time_td * pt_img_vel;//投影到像素坐标
vec_3 pt_rgb = ( ( RGB_pts * ) it->first )->get_rgb(); //地图点rgb
mat_3_3 pt_rgb_info = mat_3_3::Zero();
mat_3_3 pt_rgb_cov = ( ( RGB_pts * ) it->first )->get_rgb_cov();//地图点rgb对角协方差矩阵
for ( int i = 0; i < 3; i++ )
{
pt_rgb_info( i, i ) = 1.0 / pt_rgb_cov( i, i ) / 255; //info_rgb(map) = 1 / (cov_rgb(map) * 255)
R_mat_inv( pt_idx * err_size + i, pt_idx * err_size + i ) = pt_rgb_info( i, i );//斜对角块 R_i = 1 / (cov_pt_i_cov * 255)
// R_mat_inv( pt_idx * err_size + i, pt_idx * err_size + i ) = 1.0;
}
vec_3 obs_rgb_dx, obs_rgb_dy; //影像中x、y方向上的rgb差值
//投影点从影像插值获取rgb,计算x、y方向上的rgb差值
vec_3 obs_rgb = image->get_rgb( pt_img_proj( 0 ), pt_img_proj( 1 ), 0, &obs_rgb_dx, &obs_rgb_dy );
vec_3 photometric_err_vec = ( obs_rgb - pt_rgb ); //rgb误差: 图像对应点rgb - 地图点rgb
double huber_loss_scale = get_huber_loss_scale( photometric_err_vec.norm() ); //huber 1.0
photometric_err_vec *= huber_loss_scale;
double photometric_err = photometric_err_vec.transpose() * pt_rgb_info * photometric_err_vec; //影像误差 e^T * info_rgb(map) * e
acc_photometric_error += photometric_err;
last_reprojection_error_vec[ pt_idx ] = photometric_err;//影像误差向量索引i填充
avail_pt_count++;
// 像素坐标对相机坐标求导 ,-z^2????
mat_pre << fx / pt_3d_cam( 2 ), 0, -fx * pt_3d_cam( 0 ) / pt_3d_cam( 2 ), 0, fy / pt_3d_cam( 2 ), -fy * pt_3d_cam( 1 ) / pt_3d_cam( 2 );
mat_d_pho_d_img = mat_photometric * mat_pre;
//jacobian与vio_esikf相同
pt_hat = Sophus::SO3d::hat( ( R_imu.transpose() * ( pt_3d_w - t_imu ) ) ); //IMU系下地图点 p(IMU)^ = R(IMU <-- W) * ( p(W) - p(IMU) )
mat_A = state_iter.rot_ext_i2c.transpose() * pt_hat; //3 * 3, R(C <-- IMU) * p(imu)^
mat_B = -state_iter.rot_ext_i2c.transpose() * ( R_imu.transpose() ); // - R(C <--IMU) * R(IMU <-- W)
mat_C = Sophus::SO3d::hat( pt_3d_cam );// p(C)^
mat_D = -state_iter.rot_ext_i2c.transpose();// - R(C <-- IMU)
meas_vec.block( pt_idx * 3, 0, 3, 1 ) = photometric_err_vec ; //观测向量填充
H_mat.block( pt_idx * 3, 0, 3, 3 ) = mat_d_pho_d_img * mat_A * huber_loss_scale;
H_mat.block( pt_idx * 3, 3, 3, 3 ) = mat_d_pho_d_img * mat_B * huber_loss_scale;
if ( 1 )
{
if ( m_if_estimate_i2c_extrinsic )
{
H_mat.block( pt_idx * 3, 18, 3, 3 ) = mat_d_pho_d_img * mat_C * huber_loss_scale; //外参雅可比
H_mat.block( pt_idx * 3, 21, 3, 3 ) = mat_d_pho_d_img * mat_D * huber_loss_scale;
}
}
}
R_mat_inv_spa = R_mat_inv.sparseView();
last_avr_repro_err = acc_photometric_error;
if ( avail_pt_count < minimum_iteration_pts )
{
break;
}