设希望估计的真实函数为
f=f(X)
但是观察值会带上噪声,通常认为其均值为 0
Y=f(X)+ϵ,E[ϵ]=0
假如现在观测到一组用来训练的数据
D={(x1,y1),(x2,y2),...,(xN,yN)}
那么通过训练集估计出的函数为
f^=f^(X;D)
为简洁起见,以下均使用 f^(X) 代替 f^(X;D)
那么训练的目标是使损失函数的期望最小(期望能表明模型的泛化能力),通常损失函数使用均方误差MSE(Mean Squred Error)
E[Loss(Y,f^)]=E[MSE]=E[1N∑i=1N(yi−f^(xi))2]=1N∑i=1NE[(yi−f^(xi))2]
注意: yi 和 f^ 都是不确定的; f^ 依赖于训练集 D , yi 依赖于 xi .
下面单独来看求和式里的通项
E[(yi−f^(xi))2]=E[(yi−f(xi)+f(xi)−f^(xi))2]
=E[(yi−f(xi))2]+E[(f(xi)−f^(xi))2]+2E[(yi−f(xi))(f(xi)−f^(xi))]
=E[ϵ2]+E[(f(xi)−f^(xi))2]+2(E[yif(xi)]−E[f2(xi)]−E[yif^(xi)]+E[f(xi)f^(xi)])
=Var{noise}+E[(f(xi)−f^(xi))2]
E[yif(xi)]=f2(xi) 因为 f 和 xi 是确定的而 E[yi]=f(xi)
E[f2(xi)]=f2(xi) 因为 f 和 xi 是确定的
E[yif^(xi)]=E[(f(xi)+ϵ)f^(xi)]=E[f(xi)f^(xi)+ϵf^(xi)]=E[f(xi)f^(xi)]
E[ϵf^(xi)]=0 因为测试集中的噪声 ϵ 独立于回归函数的预测 f^(xi)
E[ϵ2]=Var{noise} 噪声方差
E[(f(xi)−f^(xi))2]=E[(f(xi)−E[f^(xi)]+E[f^(xi)]−f^(xi))2]
=E[(f(xi)−E[f^(xi)])2]+E[(E[f^(xi)]−f^(xi))2]+2E[(f(xi)−E[f^(xi)])(E[f^(xi)]−f^(xi))]
=E[(f(xi)−E[f^(xi)])2]+E[(E[f^(xi)]−f^(xi))2]+2(E[f(xi)E[f^(xi)]]−E[E[f^(xi)]2]−E[f(xi)f^(xi)]+E[E[f^(xi)]f^(xi)])
=bias2{f^(xi)}+variance{f^(xi)}
E[f(xi)E[f^(xi)]]=f(xi)E[f^(xi)] 因为 f 是确定的
E[E[f^(xi)]2]=E[f^(xi)]2
E[f(xi)f^(xi)]=f(xi)E[f^(xi)] 因为 f 是确定的
E[E[f^(xi)]f^(xi)]=E[f^(xi)]2
E[(f(xi)−E[f^(xi)])2]=bias2{f^(xi)} 偏差
E[(E[f^(xi)]−f^(xi))2]=variance{f^(xi)} 方差
最终
因此,要使损失函数的期望 E[Loss(Y,f^)] 最小,既可以降低bias,也可以减少variance。这也是为什么有偏的算法在一定条件下比无偏的算法更好。
偏差 bias 描述的是算法依靠自身能力进行预测的平均准确程度
方差 variance 则度量了算法在不同训练集上表现出来的差异程度
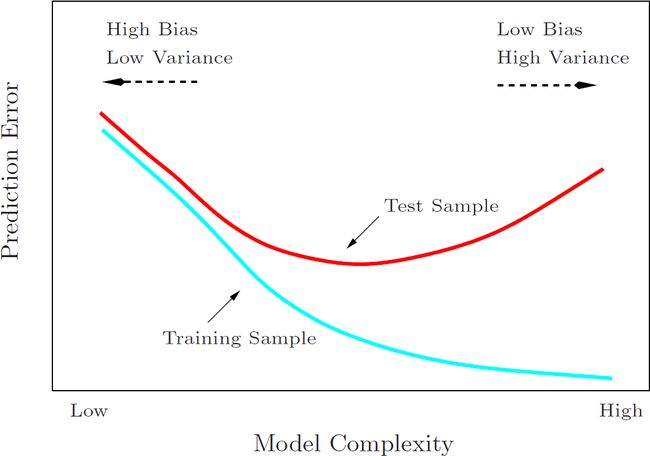
下面来自The Elements of Statistical Learning P38 Figure 2.11 的图则阐释了模型复杂度与偏差、方差、误差之间的关系:
PS:
装袋算法Bagging通过bootstrap对训练集重采样来并行训练多个分类器(均匀采样),主要是降低方差 variance。
提升算法Boosting通过迭代调整样本权重来串行组合加权分类器(根据错误率采样),因而主要是降低偏差 bias(同时也减少方差 variance)。