233搞懂HMM（隐马尔可夫）

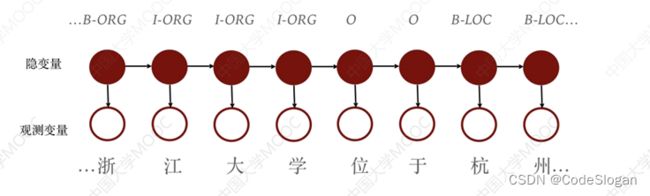
有向图模型，主要用于时序数据建模，在语音识别，自然语言处理等领域，以及在知识图谱命名实体识别中的序列标注，有广泛应用。

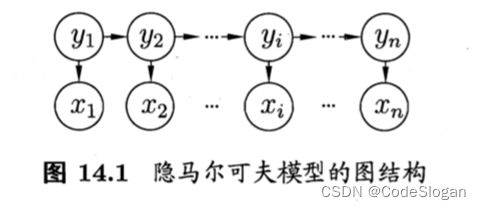
HMM模型由两部分组成， 观测变量x与 状态变量y。其中状态变量又称为隐变量，常常被作为序列标注结果

2条性质

马尔可夫链性质：

1. t时刻的状态变量y只由t-1时刻的状态决定，而与t-2及之前的无关
2. t时刻的观测变量仅由t时刻的状态变量决定

3个参数

1. 状态转移概率矩阵：
   为NxN的矩阵，矩阵里的每个值记录从当前状态转移到其它状态的概率
2. 输出观测概率矩阵：
   为NxM的矩阵，M为观测值结果的个数
   矩阵记录从当前状态到每一个观测值的概率
3. 初始状态概率
   在t=1初始时刻，各状态出现的概率。

---

给定隐马尔可夫模型$\lambda$，生成观测序列的过程：

1. 设置t=1，根据初始状态概率参数，选择初始状态
2. 根据输出观测概率矩阵，得出当前状态变量的观测变量
3. 根据状态转移概率矩阵，得出当前状态变量的下一个状态变量
4. 重复2-3过程，直到结束

3个问题

1. 概率计算问题。给定模型$\lambda =\left(A,B,\pi \right)$和观测序列$O＝o_1，o_2,\dots ,o_T$，计算在模型$\lambda$下观测序列$O$出现的概率$P\left(O|\lambda \right)$。前向-后向算法是通过递推地计算前向-后向概率可以高效地进行隐马尔可夫模型的概率计算。

2. 学习问题。已知观测序列$O＝o_1，o_2,\dots ,o_T$，估计模型$\lambda =\left(A,B,\pi \right)$参数，使得在该模型下观测序列概率$P\left(O|\lambda \right)$最大。即用极大似然估计的方法估计参数。EM算法可以高效地对隐马尔可夫模型进行训练。它是一种非监督学习算法。

3. 预测问题。已知模型$\lambda =\left(A,B,\pi \right)$和观测序列$O＝o_1，o_2,\dots ,o_T$，求对给定观测序列条件概率$P\left(I|O\right)$最大的状态序列$I＝i_1，i_2,\dots ,i_T$。维特比算法应用动态规划高效地求解最优路径，即概率最大的状态序列。

维特比算法

输入：HMM模型参数，观测序列
输出：状态序列
算法流程：
时刻由观测序列长度决定
$\delta$用于记录每一时刻各状态的概率
$\psi$用于记录前一个时刻的状态，便于回溯

1. 初始化，$\delta$和$\psi$，$\psi$置为0
2. 递归（动态规则，状态转移矩阵），
   现有t-1时刻，各状态出现的概率。
   根据状态转移矩阵，分别计算其转移到各个状态的概率，取最大值乘以输出观测概率
3. 取累乘概率的最大值，并进行回溯，得到状态序列

class HiddenMarkov:
    def __self__(self):
        self.alphas = None
        self.forward_P = None
        self.betas = None
        self.backward_P = None
        
    def viterbi(self, Q, V, A, B, O, PI):
        # 状态集合的大小
        N = len(Q)
        # 观测序列的大小
        M = len(O)
        
        deltas = np.zeros((N, M))
        psi = np.zeros((N, M))
        I = np.zeros((1, M))
        
        # 遍历预测序列，即遍历全部时刻
        for t in range(M):
            # 得到这个观测序列值在观测集合里的索引 
            idxO= V.index(O[t])
            
            # 每一个时刻遍历所有状态
            for i in range(N):
                if t == 0:
                    deltas[i][t] = PI[0][i] * B[i][idxO]
                    psi[i][t] = 0
                else:
                    # t-1时刻所有的状态 与 转移到第i个状态的概率 对应相乘取最大值
                    # 再与输出预测相乘
                    deltas[i][t] = np.max(
                       np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A])) * B[i][idxO]
                    
                    psi[i][t] = np.argmax(
                       np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A]))
        # 得到最后一时刻的最大概率的下标
        I[0][M-1] = np.argmax([delta[M-1] for delta in deltas])
        # 由后向前递归得到其它结点
        for t in range(M - 2, -1, -1):
            I[0][t] = psi[int(I[0][t+1])][t+1]
        
        # 输出最优路径
        print('最优路径是：', "->".join([str(int(i + 1)) for i in I[0]]))

Q = [1, 2, 3]  # 状态序列
V = ['红', '白']
A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]] # 状态转移
B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]  # 输出观测
O = ['红', '白', '红']  # 观测序列
PI = [[0.2, 0.4, 0.4]]  # 初始概率分布

HMM = HiddenMarkov()
HMM.viterbi(Q, V, A, B, O, PI)

参考资料

1. 《机器学习》周志华
2. 《统计学习方法》李航
3. 统计学习方法代码实现