Kmean(k均值聚类)学习-matlab代码撰写-2022-08-09
对于k均值的学习,来自于以下的博主,非常的感谢
看不懂打我系列之K-means聚类算法及其MATLAB实现_能让你开心的小技巧的博客-CSDN博客
所以,博主再这里不阐述k均值的原理了,直接进行了代码优化和代码冗余的修改,所有注释都有,可以直接吃和改进。
可以直接用于三维点云的聚类,由于博主这里没有适合kmean的聚类数据,就用matlab软件中带的数据进行示例了,上代码:
1 Kmean代码
clear;clc;
% 提取matlab2019b软件数据
rng default;
data = [randn(100,2)*0.75+ones(100,2);
randn(100,2)*0.5-ones(100,2)];
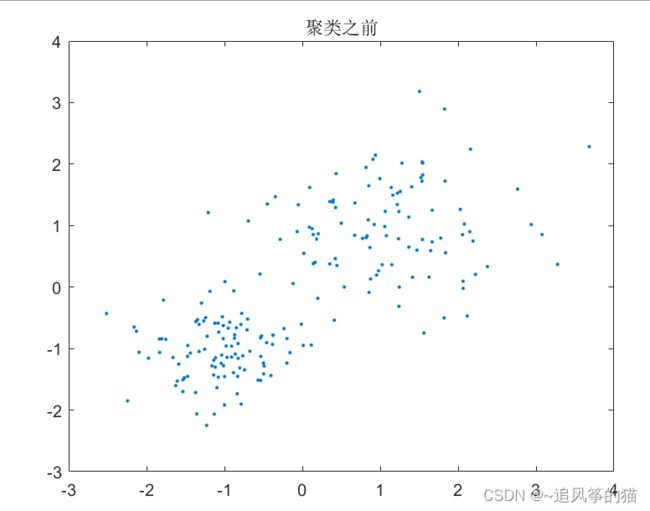
figure;
plot(data(:,1),data(:,2),'.');
% 计算数据的维度
[m,n] = size(data);
% 制作聚类索引
idx = zeros(m,1);
% 设置聚类数量
k = 2;
% 随机选取聚类中心
center = randi(m,k,1);
center = data(center,:);
while true
% 储存新的中心
nwe_center = zeros(k,n);
for i = 1:k
%d(:,i) = sqrt((data(:,1)-center(i,1)).^2+(data(:,2)-center(i,2)).^2);
% 计算每个点到聚类中心的距离
d(:,i) = sqrt(sum((data-center(i,:)).^2,2));
end
% 根据每个点到聚类中心的聚类,选取最小值,进行分类
[~,idx] = min(d,[],2);
N = 0;
% 循环聚类个数
for j = 1:k
% 寻找满足聚类索引值的点
temp = data(idx==j,:);
% 计算当前聚类点的坐标总和
new_center(j,:) = sum(temp);
% 计算当前聚类点的坐标平均值
new_center(j,:) = new_center(j,:)/length(temp(:,1));
% 判断新的中心点和原始的中心点的差别大小,满足条件则聚类
if norm(new_center(j,:)-center(j,:))<0.1
% 如果满足阈值条件,则聚类符合,个数+1
N=N+1;
end
end
if N==k
break
else
% 不满足聚类个数,则更新中心点(偏移中心点)
% 进行新的迭代
center = new_center;
end
end
plot(data(idx==1,1),data(idx==1,2),'b.');
hold on;
plot(data(idx==2,1),data(idx==2,2),'r.');
grid on;
plot(center(:,1),center(:,2),'kx',...
'MarkerSize',15,'LineWidth',3)
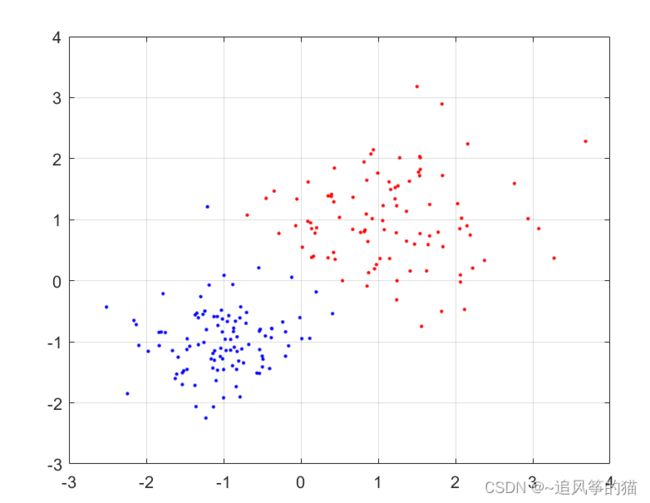
根据代码,最后聚类得到的:
2 matlab2019b自带kmeans函数
matlab2019b自带k均值函数,kmeans,用法如下
idx = kmeans(X,k)
idx = kmeans(X,k,Name,Value)
[idx,C] = kmeans(___)
[idx,C,sumd] = kmeans(___)
[idx,C,sumd,D] = kmeans(___)
上代码:
clear;clc;
% 提取matlab2019b软件数据
rng default;
data = [randn(100,2)*0.75+ones(100,2);
randn(100,2)*0.5-ones(100,2)];
figure;
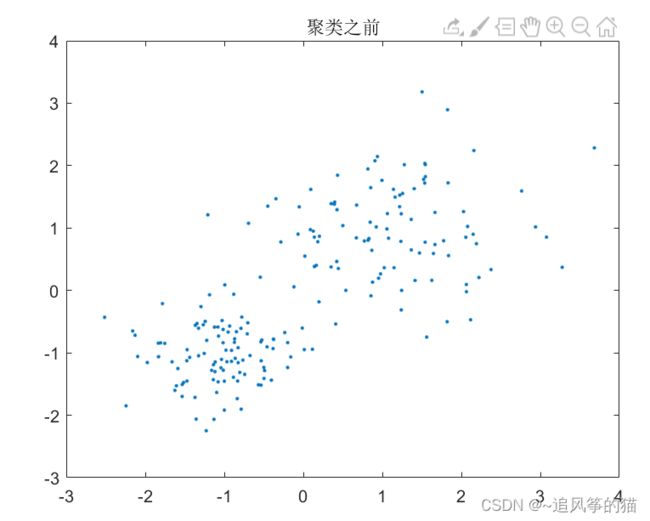
plot(data(:,1),data(:,2),'.');
title '聚类之前';
idxk = kmeans(data,2);
plot(data(idxk==1,1),data(idxk==1,2),'b.');
hold on;
plot(data(idxk==2,1),data(idxk==2,2),'r.');
grid on;结果如下:
可以看得出来还是存在差异的。