GIRAFFE: Representing Scenes as Compositional Generative Neural Feature Fields(CVPR2021 Best paper)

1. 简介

1.1 参考资料

2021年的最佳论文颁给了这篇GIRAFFE，是一篇关于隐式三维重建的工作，本博客主要参考资料：

1. 《从NeRF -> GRAF -> GIRAFFE，2021 CVPR Best Paper诞生记》（知乎专栏一篇文章，链接点击此处）
2. 《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》ECCV 2020，简称为NeRF
3. 《GRAF: Generative Radiance Fields for 3D-Aware Image Synthesis》NeurIPS 2020，简称为GRAF
4. 《GIRAFFE: Representing Scenes as Compositional Generative Neural Feature Fields》CVPR 2021，也就是今天要讲的文章

1.2 课题研究背景（个人理解）

现代计算机图形学的发展已经能够合成逼真的物体与场景，但是代价却是需要昂贵的硬件成本，并且前期的美工建模需要耗费大量的人力物力。为了有效解决这一困境，需要解决三个问题：

1. 如何让电脑自动生成物体，替代人工绘制
2. 如何将生成的物体渲染成真实的二维图像
3. 让我可以自由编辑物体的各种属性（更专业一点：表征的解耦，disentangle representation），不然我生成物体也没啥作用

GAN的发展为第一个问题的解决创造了条件，可微渲染和神经渲染的发展为第二个问题的解决创造了条件，而第三个问题却仍在探索之中

• 关于可微渲染与神经渲染的个人理解：

1. 渲染方式可以大致分为面渲染与体渲染，面渲染类似于图形学中的栅格化渲染，将顶点与三角形这些离散的数据变成图像离散的RGB数值，在渲染管线中只有栅格化这一步骤是不可微的，所以许多可微渲染的文章在这里做研究，通过各种途径将这一步变成可微的（参考DIB-R，NeurIPS 2019）；而体渲染的方式因为本身就是由积分组成，天生可微
2. 而神经渲染，顾名思义是让一个神经网络充当渲染器，但是牵扯到场景的表示问题，所以并不是简单的把一个本能够正常栅格化渲染的场景当做神经网络的输入。关于神经渲染具体举例，可以是将styleGAN进行改造（参考《Inverting Generative Adversarial Renderer for Face Reconstruction》CVPR 2021 Oral），让latent code作为输入，去生成真实感的图像

1.3 文章发展脉络

按照这条时间线：NeRF—>GRAF—>GIRAFFE，形成了这篇论文，可以说这篇论文就是在NeRF相关的后续研究工作中取得突破性进展的一篇文章，而为了便于理解，本博客也将在介绍NeRF、GRAF之后，再介绍这篇GIRAFFE

2. NeRF

2.1 解决的问题

给定几张相机从不同角度拍摄同一个物体（比如说一个架子鼓）的照片，这些照片还有相机的位姿参数都是已知的，要做的事情是生成一个新的角度拍摄得到的物体照片，这个新的角度是我们想要的任意角度

2.2 解决方法

NeRF方法针对这个问题的解决方案是：使用神经辐射场（neural radiance field）来表示我们想要三维重建的物体，神经指的是神经网络（MLP），用一种隐式的方法表示三维场景，辐射可以理解为我们照的照片每个像素都射出来一根光线打到这个三维物体上，把这每根光线应该有的颜色给分别计算出来，就实现了渲染

2.2.1 场景表示

假设我们要重建的是一个未知的场景，有一根光线打了上去，这根光线上有无穷多个点，每个点都有对应的三维坐标$x=(x,y,z)$与视线方向$d=(\theta ,\varphi )$（要表示空间中的一条直线的方向，只需要两个自由度即可，和经纬度一样，而对于这根光线上的所有点来说，$d$肯定都是一样的），假设有这么一个神经网络，根据这5个维度的任意输入，都能输出对应的RGB数值与体积密度，那么我们就能用这个神经网络来隐式地表示一个场景：
$F_{\theta }:(x,d)\to (c,\sigma )$
而至于如何去优化这个场景以尽可能逼近我们想要的场景，优化参数$\theta$即可
注意以下几点：

1. 对于空间中的每一个确定的点，该点对应的体积密度是确定的，但是颜色却不一定，和我们的观察方向有关，因为这样才能让我们的重建满足各种光照效果
2. 神经网络使用MLP，先将输入的$(x,y,z)$转换成$\sigma$和中间特征，之后再把中间特征和$d$结合得到点在某个视线方向下的颜色值
3. 一个场景仅仅使用一个模型来表示
   如下图所示：
   
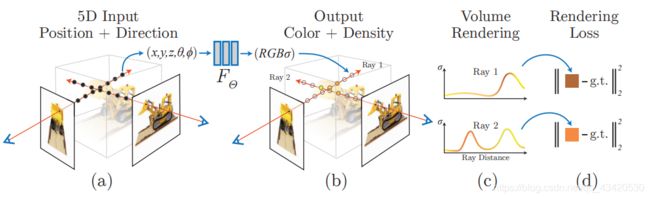
   经过体渲染之后，我们比较渲染图和真实图像的差异，就能够优化场景表示了。

2.2.2 渲染成图像

场景的表示问题解决了，接下来就是如何渲染出我们想要的图像了，假设我们要渲染一张$256\ast 256$的照片，那么就用$256\ast 256$根光线打上去就行，具体方向如何取决于我们想要的相机位姿，而对于每一根光线的颜色该如何计算，很自然就能联想到体渲染：

其中$C(r)$代表光线$r(t)=o+td$的最终反映在像素上的颜色，$r(t)$中的$t$决定了光线上的某个点的具体位置，在渲染的时候划分出近点$t_n$和远点$t_f$作为积分的边界，整个体渲染是一个积分形式，把一根光线上无穷多个点进行累加，就可以得到每个像素具体的颜色。为了方便我们定性的理解，我们分三部分：

1. $T(t)$是一个关于$t$的函数，随着$t$的增大（由近至远），数值从1下降向0靠近，可以理解为透光率，也就是说从近点开始走光线不会打到任何粒子的概率
2. $\sigma (r(t))$是点的体密度，可以理解为在某个点终止的概率，我们从直观上很容易理解，体密度越大的地方，光线在这个点终止的概率越大
3. $c(r(t),d)$是点的颜色，不仅和点的位置有关，还和我们这根光线的方向有关

如何定性地理解这个体渲染式子呢，$\sigma$和$c$相乘我们可以看做是求了个这条光线上无穷多个点颜色出现概率的数学期望，而再与T相乘可以认为赋予了靠前的点颜色更大的比重（emmm有点合理hhh）

原理是这样，但是神经网络可无法做到连续的输出，因此体渲染采取了离散的方式进行点的累加：

先将近点与远点划分成等间距的N段，之后在这每一段里进行点的随机均匀采样，总共下来采样了N个点，求积分的式子也被改写成了上述求和的式子

2.2.3 优化

2.2.3.1 位置编码

上图可以看出，如果仅仅使用上面的方式进行三维重建，在高频区域并无法取得好的效果（第四张图挖掘机的履带），尽管神经网络是万能函数近似器，但是它更倾向于学习低频特征，如果在输入信息传递给网络之前，使用高频函数将输入信息映射到更高维度的空间，可以更好地拟合包含高频变化的数据，这里有两篇参考文章《On the spectral bias of neural networks》ICML2018 ，《 Fourier features let networks learn high frequency functions in low dimensional domains》NeurIPS 2020。
因此在把输入丢进神经网络之前，先把它升高几个维度：

其中$L$决定了维度的数量，$p$是位置$x$或方向$d$的三个组成部分之一，位置的三个组成部分是$(x,y,z)$三个坐标，方向的组成部分是方向向量的三个坐标分量。之所以这么做应该是和傅里叶变换有关，这里提供一个定性的理解：神经网络本身对微小的变化不敏感，如果这样改进之后，原本输入的微小变化改进成了输入的剧烈变化，那么就会导致神经网络输出的剧烈变化，也就能反映高频信息了。

2.2.3.2 分层采样

之前的采样方式是在划分出的N个区域内均匀采样求和，但是我们肯定希望密度越大的地方采样越多越好，并且在物体之外的采样点也没啥大的作用，也能减小开销，因此设计了这种分层采样方式。使用两个网络同时进行训练 (后称 coarse 和 fine 网络)， coarse 网络输入的点是通过对光线均匀采样得到的，根据 coarse 网络预测的体密度值，对光线的分布进行估计，然后根据估计出的分布进行第二次重要性采样，然后再把所有的采样点一起输入到 fine 网络进行预测（同时优化coarse和fine）

3. GRAF

3.1 简介

GRAF，Generative Radiance Fields，生成辐射场，研究的起因如下：

在3D感知图像生成（3D-aware image synthesis）这一领域中（差不多都基于GAN），把三维的物体进行离散化的表示，比如PlatonicGAN的体素表示， HoloGAN的三维特征表示，体素表示法会限制分辨率，分辨率升高时会占用内存，并且产生可见的伪影（artifacts），特征表示法虽然好一点，但是需要额外学习如何渲染，把抽象的三维特征映射到二维的RGB数值，导致了特征很难解耦，在高分辨率下很难保持视图一致性

而NeRF那样的模型，虽然三维重建的效果不错，但是缺点在于：需要大量的同一个场景物体的不同角度拍摄数据，这些数据还得有三维标注（相机位姿）；无法自由编辑重建物体
所以，GRAF算是在NeRF工作的基础上，结合了GAN进行了一番研究工作，这样就能使用二维监督的方式进行三维重建（也就是说仅仅需要同一物体的不同角度照片即可，不再需要相机位姿参数），让GAN去猜相机位姿势啥样的，并且对物体的形状与颜色可控性上面做了一定贡献

3.2 方法

3.2.1 NeRF相关公式

首先用几个简洁的公式概括NeRF的核心框架：

1. 位置编码操作，p代表位置与方向各三个组成部分之一
   
2. NeRF模型的数学解释，看做是$L_x$维度（空间坐标的位置编码后的维度）与$L_d$维度（方向经过位置编码后的维度）到三维（RGB）与一维（体密度）的映射
   
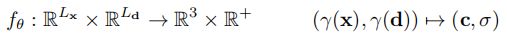
3. 体渲染公式，针对每根光线，将采样点三维的RGB与一维的体密度映射到渲染图像像素三维的RGB，需要进行N次操作，N就代表要渲染出图像的像素数；体渲染具体的过程如第二行所示
   
   

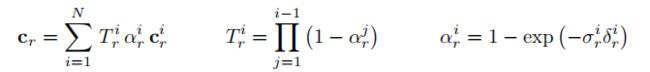
3.2.2 GRAF框架

图中的N代表每根光线采样点数量，R代表像素（光线）数量，总的来说，针对NeRF的改进有三点

1. 借助GAN的设计思想，引入相机位姿的分布$\xi$（相机位置从半球进行均匀采样，确保始终对准圆心，距离也进行均匀采样）、物体形状的分布$z_s$、物体外观的分布$z_a$让网络学习
2. 为了在训练阶段节省计算量，使用ray sampling方式进行像素（光线）的选择
3. 整个网络需要训练的部分为图中的$g_{\theta }$，在NeRF的MLP基础上融合进了$z_s$与$z_a$

3.2.2.1 ray sampling

这里的ray sampling指的并不是针对每根光线上一系列点的采样，而是为了节省训练阶段的计算量，对我们要准备渲染的图像的像素的一种采样方式，看图很容易理解：

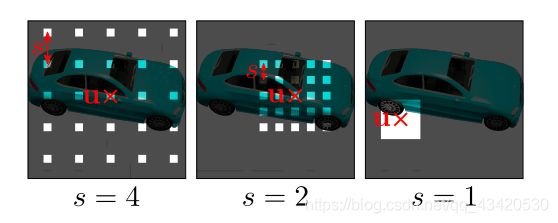
使用$v=(u,s)$来决定如何进行像素的采样，$u$代表采样点的中心，$s$代表采样点的间距，再选一个合适的$K$值反映采样点的数量（如上图的$K=5$），最终采样出来的像素合并成一张新的图像，称为patch,patch的大小为$K\ast K$，而我们训练阶段总共要准备积分的光线数为$R=K^2$条，在训练好后的推理阶段光线数为$R=W\ast H$条，$W$与$H$为要生成图像的宽与高
有两个值得注意的地方：

1. 使用$K\ast K$的patch进行采样，一方面节省了训练复杂度，一方面还可以不再受图像分辨率限制，后面始终用一个固定大小的鉴别器进行评估即可
2. $v=(u,s)$在GRAF结构中两个地方被用到了，前面部分用于渲染图像的生成（准确的说是渲染patch），后面部分用于从训练数据中提取patch的ground truth
3. patch坐标$u,s$是实数，不是整数，是物理坐标，而非像素坐标，训练阶段从输入图像提取patch的ground truth的时候使用双线性插值提取
4. 训练时先用大的接受域捕捉全局信息（较大的s），再用小的接受域捕捉高频信息(较小的s)

3.2.2.2 Conditional Radiance Field

这是整个GRAF框架的核心部分，称作条件辐射场，至于为什么要加“条件”两个字，是因为该辐射场与物体的形状编码$z_s$和外观编码$z_a$有关，如果说NeRF使用神经网络表示整个场景，那么GRAF的神经网络更像是一个受输入参数控制的场景。

整个条件辐射场记为$g_{\theta }$，划分为三个部分$h_{\theta },c_{\theta },{\sigma }_{\theta }$，其实除去$z_s,z_a$，和NeRF的辐射场就差不多了，用公式表示如下：

3.2.2.3 鉴别器与训练

最终的损失函数其实相当于GAN的损失函数，公式如下：

其中的$f(t)=-log(1+exp(-t))$很眼熟，不用再多说
在训练阶段，我们给许多张同一个物体从不同角度拍摄的照片，为了节省计算，生成器与鉴别器使用相同的ray sampling得到的patch，比较渲染图像与真实图像patch的差异，优化条件神经场$g_{\theta }$参数；在推理阶段，我们随机采样$z_s,z_a,\xi$，之后继续按照流程渲染出一张完整的图像，就相当于“无中生有”一般，确定好了一个相机角度，拍摄一张网络从数据中学习到的三维场景

3.3 不足之处

在GRAF最后的总结中作者指出了该方法仅仅对场景中的单一物体起作用，无法处理多物体情况

4. GIRAFFE

了解了NeRF和GRAF的工作之后，GIRAFFE的工作理解起来就很容易了

4.1 简介

论文题目：Representing Scenes as Compositional Generative Neural Feature Fields，我们先来分析一下，是使用组合的生成神经特征场来表示一个多物体场景，与GRAF的不同的地方有两个关键词：组合的、特征场
实际上，与GRAF不同的地方也主要有两处：

1. 组合的：把GRAF使用一整个模型才能表示的场景给组合起来， 也就是说场景中有多少个物体，就用多少个GRAF，有效地解决处理多物体重建时无法自由编辑每个单一物体的情况
2. 特征场：与GRAF不同，最终分别使用GRAF表示单个物体的时候，因为后面还要把他们组合起来，所以把采样点的颜色替换成颜色特征，然后组合成一个新的特征图，之后再使用设计的神经网络渲染渲染出最终RGB图像

4.2 研究动机与灵感

给定一个有多个物体的三维场景，许多场景合成方法的解耦操作是在2D空间进行的，没有考虑到场景实际上是3维的，因此会导致编辑物体的时候产生问题

如第一行所示，许多没有在他们方法里考虑物体的三维属性的方法，操作多物体场景时，比如只想把左边的物体往前移动，结果导致的右边的物体产生了变化，这便是没有有效地将特征解耦
而GIRAFFE因此有两个灵感来源（insight）

1. 将合成的3D场景表示直接融入生成模型中，可以实现更可控的图像合成
2. 将这种显式的3D表示（体渲染得到的特征图）与神经渲染相结合，可以更快地进行推断，使图像更加真实

4.3 方法

4.3.1 生成神经特征场

GRAF框架的核心部分可概括成如下公式：

而GIRAFFE可以看做是多个GRAF的组合，其中每个GRAF的改变如下：

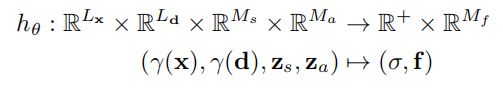
可以看到改变的地方是将原先三通道RGB（代表每个点的某个视线方向的颜色）替换成了$M_f$通道的特征。场景中有多少个物体（背景也单独算一个），就用多少个这样的GRAF

这时我们要注意一个坐标系的问题，因为表示一个物体，所以在GRAF里的射线采样点坐标系不仅可以看做局部坐标，也可以看做全局坐标；但是GIRAFFE因为牵扯到场景组合的问题，在生成模型生成一条光线打到不同物体上的时候，采样点使用的是全局坐标，而我们为了将来评估每个GRAF表示物体的时候，需要采样点的局部坐标，因此还需要进行一次仿射变换：

用文章中的话来说：我们在场景空间中（也就是全局坐标）进行体积渲染，并在其标准对象空间（也就是局部坐标）中评估特征场，更完整的公式如下：

$k(x)$表示将采样点从局部坐标变换到全局坐标，$k^{-1}(x)$是将采样点从全局坐标变换到局部坐标，式子左侧的属性其实就是在局部坐标下的物体体密度与颜色特征属性

4.3.2 特征场组合

现在面临一种情况，因为是多物体场景，全局坐标下的同一个采样点，会采样不同的物体，该如何表示这些物体组合后的最终体密度与颜色特征呢，这里使用如下公式进行组合：

按照体密度之间的比重，进行颜色特征的加权，符合常规认知

4.3.3 体渲染

有了全局坐标下组合后场景的每个光线采样点的体密度与颜色特征，接下来一步自然就到了体渲染阶段，公式如下：

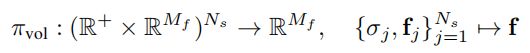
其中的$N_s$代表光线上采样点数量，最终渲染得到的，依旧不是GRB颜色，而是颜色特征图，原文中这样描述：我们体积渲染场景到一个相对低分辨率的特征图像，以节省时间和计算，神经渲染器再处理特征图像并输出最终效果图

4.3.4 神经渲染

其中$H_V$与$W_V$是体渲染特征图较小的分辨率，经过神经网络渲染得到最终的RGB图像，结构如下：

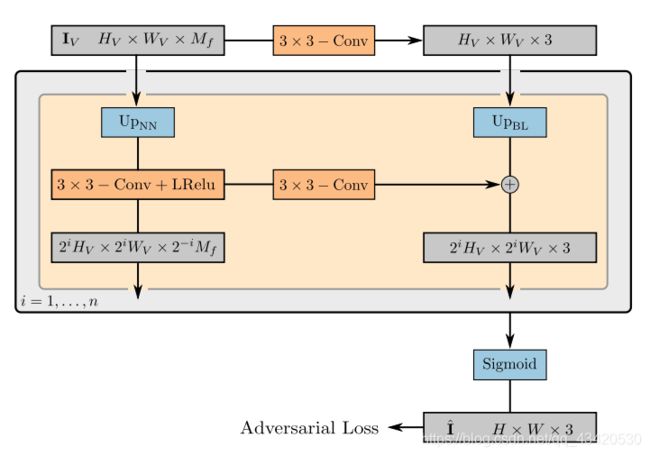
这种结构文中说是从styleGAN中借鉴的思想，可以看到左边一列是特征图依次上卷积，而右边一列则是一系列从小到大分辨率的最终渲染图像，最终渲染图像从小到大的分辨率变化并不是因为上卷积，而是双线性插值上采样，毕竟都是渲染出的真实图像了，如果继续卷积应该也不符合常理，更应该按照真实图像的处理过程来。另外注意相同层级的特征图与渲染图彼此之间都会进行结合。

4.4 总结

放一张GIRAFFE的总体结构

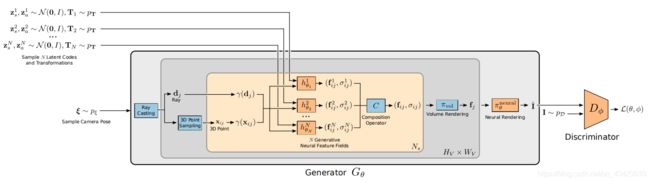
结合NeRF与GRAF的工作，再仔细品味GIRAFFE，其实也不算难以理解，因为本项工作正是与它们一脉相承发展而来。并且我们发现其中的大部分内容都是基于我们直观的物理经验，在无法用物理公式处理的地方，就让神经网络发挥作用。
我们都知道，GAN的一大研究挑战便是如何让latent code进行解耦以变得可控，而多数工作便是通过精心设计各种损失函数与先验假设来实现，本文拥有如此多不同的latent code，也没有什么比较新颖的损失函数，是如何让它们各司其职，实现解耦的呢？
我想答案便是实现模型的过程中引入了对真实世界的物理建模，本身便形成了各种约束！
（关于用神经网络表示场景与普通的神经网络的区别这里我也写了篇思考）