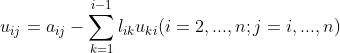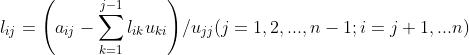C语言——利用矩阵LU分解法求逆、行列式
本章介绍了LU分解法,以及如何利用LU分解法求逆、行列式,针对每个公式、原理、代码进行了详细介绍,希望可以给大家带来帮助。
目录
LU分解法
概念
确定L、U矩阵
LU分解法的意义
程序设计
LUP求逆
1)代码
2)代码讲解
3)高斯法求逆
4)矩阵乘法
LUP求行列式
1)代码
2)代码讲解
LU分解法
概念
将系数矩阵A转变成等价两个矩阵L和U的乘积 ,其中L和U分别是单位下三角矩阵和上三角矩阵。当A的所有顺序主子式都不为0时,矩阵A可以唯一地分解为A=LU。其中L是下三角矩阵(主对角线元素为1),U是上三角矩阵。
![]()
于是,对矩阵A求逆就变成了:
![]()
因为LU分别为下三角矩阵和上三角矩阵,再进行高斯变换求逆矩阵时,浮点运算的复杂度将减少一半。
对矩阵A求其行列式的值变成:
![]()
因为U的主对角元素全1,故 A的行列式的值等于U主对角线元素的乘积。
确定L、U矩阵
因为矩阵L的主对角元素定死为1,因此可以通过矩阵乘法原理,逐行、逐列的逆推出矩阵L和U的元素
方法如下:
- 确定U的第一行
- 确定L的第一列
- 确定U的第二行
- 确定L的第二列
- ...
- 确定U的第n行
- 确定L的第n列
确定U的第一行:
- L的第一行与U的第一列对应元素相乘再相加,结果等于
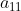 ,即:
,即: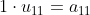
- L的第一行与U的第二列对应元素相乘再相加,结果等于
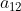 ,即:
,即: 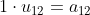
- 不难看出,U的第一行与A的第一行元素相同:
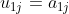
确定L的第一列:
仿照上述步骤,即可求出L、U,整理公式如下:
在进行代码设计时,求和部分可用for循环单独计算,存储到变量a中,变量a需初始化为0,当i=0时,不满足for循环条件,a=0,即可推出上述U的第一行和L的第一列。
LU分解法的推导与验证请参考相关数值分析教材,推荐参考博客矩阵的直接LU分解法
LU分解法的意义
- LU具有承袭性,这是LU的优点。
- LU只适用于解所有顺序主子式都大于0的,通用性欠缺,这是LU的缺点。
- LU法不保证具有数值稳定性,这是LU的缺点。(Gauss法可以用选取列主元技巧保证数值稳定性)
集合LU与Gauss优点,同时规避掉这些缺点的,是LUP分解法。
作者:寨森Lambda-CDM
我个人的理解是:计算机在处理超维矩阵时(例如一万维),会采用分块矩阵的方式进行求解,通过先分块再LU,将矩阵分成一块块下三角矩阵![]() 和上三角矩阵
和上三角矩阵![]() 存储起来,在后续其他计算中,直接调用下三角矩阵和上三角矩阵计算的效率更高。(该部分我也在学习,欢迎大家讨论)
存储起来,在后续其他计算中,直接调用下三角矩阵和上三角矩阵计算的效率更高。(该部分我也在学习,欢迎大家讨论)
程序设计
该部分程序实际上是LUP分解法,增加了选择主元的过程,因为在分解LU以及高斯消元求逆时,如果主元的元素是0,那么计算机将无法计算,所以在分解前需先选择主元。
LUP求逆
1)代码
#include
#include
#include
#include
double** Matrix_LU_Inv(double** src)
{
if (src == NULL)exit(-1);
int row = (int)_msize(src) / (int)sizeof(src[0]);
int col = (int)_msize(*src) / (int)sizeof(src[0][0]);
if (row != col)exit(-1);
int i, j,k,max;
double** L, ** U, ** tmp,**Linv,**Uinv,**res,Lsum, Usum,p;
L = (double**)malloc(sizeof(double*) * row);
U = (double**)malloc(sizeof(double*) * row);
tmp = (double**)malloc(sizeof(double*) * row);
if (L && U)
{
for (i = 0; i < row; i++)
{
L[i] = (double*)malloc(sizeof(double) * col);
U[i] = (double*)malloc(sizeof(double) * col);
tmp[i] = (double*)malloc(sizeof(double) * col);
memset(L[i], 0, sizeof(L[0][0]) * col);//L U需初始化为0
memset(U[i], 0, sizeof(U[0][0]) * col);
memcpy(tmp[i], src[i], sizeof(src[0][0]) * col);//拷贝数据
}
}
for (i = 0; i < row; i++)
{
for (j = 0; j < row; j++)
{
if(i==j)
L[i][j] = 1;//L主对角线为1
}
}
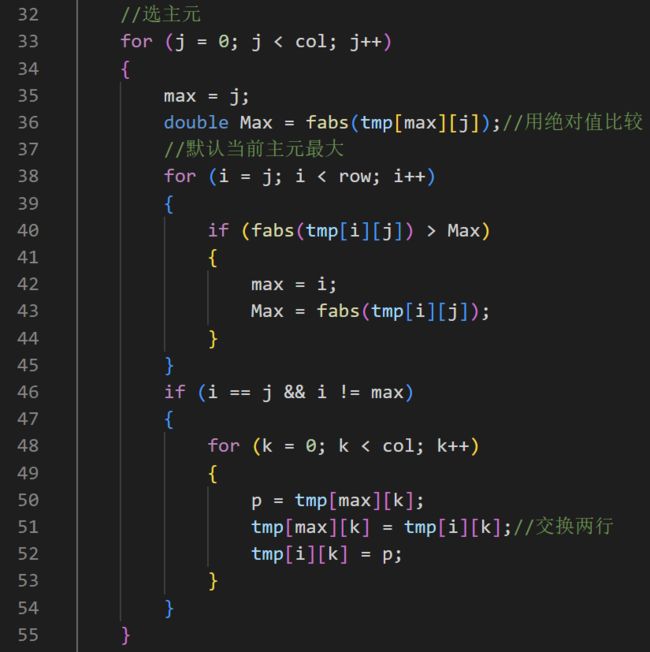
//选主元
for (j = 0; j < col; j++)
{
max = j;
double Max = fabs(tmp[max][j]);//用绝对值比较
//默认当前主元最大
for (i = j; i < row; i++)
{
if (fabs(tmp[i][j]) > Max)
{
max = i;
Max = fabs(tmp[i][j]);
}
}
if (i == j && i != max)
{
for (k = 0; k < col; k++)
{
p = tmp[max][k];
tmp[max][k] = tmp[i][k];//交换两行
tmp[i][k] = p;
}
}
}
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
if (i <= j)
{
Usum = 0;
for (k = 0; k < i ; k++)
{
Usum += L[i][k] * U[k][j];//计算求和部分
}
U[i][j] = tmp[i][j] - Usum;
}
else
{
Lsum = 0;
for (k = 0; k < j ; k++)
{
Lsum += L[i][k] * U[k][j];//计算求和部分
}
L[i][j] = (tmp[i][j] - Lsum) / U[j][j];
}
}
}
Linv = Matrix_inver(L);//求逆
Uinv = Matrix_inver(U);
res = Matrix_Mul(Uinv, Linv);//乘法
free(L);free(Linv);free(U);free(Uinv);free(tmp);
return res;
} 2)代码讲解
第3行:判断传入矩阵的指针是否为空
第4~6行:判断矩阵维数,_msize为
第7行:i,j,k为用于循环的变量 ,max为选主元时记录最大数所在的行数
第8行:L,U对应L U矩阵;tmp为为保护原矩阵所创建的临时矩阵;Linv,Uinv对应其逆矩阵;res为最终输出的逆矩阵;Lsum和Usum分别对应公式中求和部分;p为用于交换两行元素的临时变量
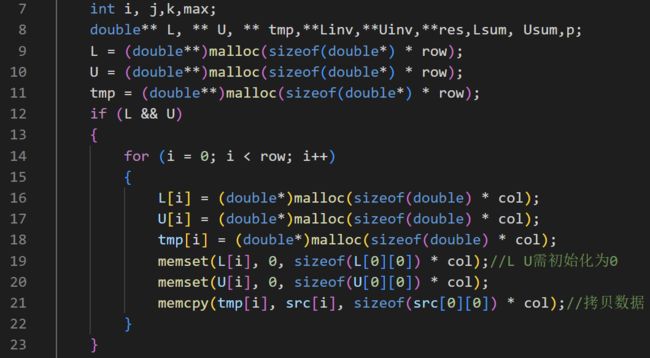
第9~23行:为上述矩阵开辟内存空间,并将L、U初始化为0,将原矩阵内容拷贝到tmp中
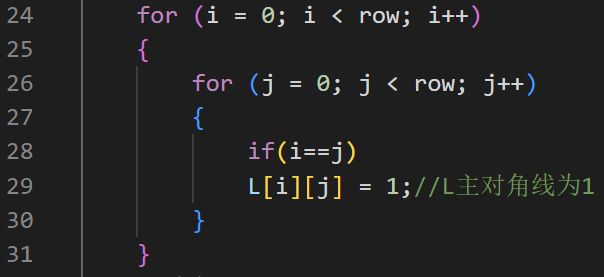
第24~31行:将L主对角元素化为1
第33~55行:选择主元,默认当前主元最大,从主对角线下方选择主元(保护选过的主元)。
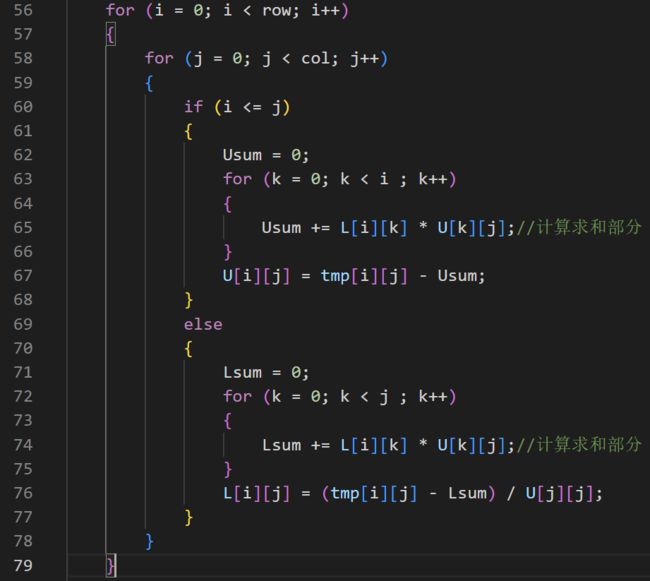
第60行:因为在计算LU时,是先计算U的行,再计算L的列,进行交替计算的;只需判断行号i和列号j的大小:i <= j 时,需要计算的元素在主对角线上方,计算U;反之,在主对角线下方计算L(因为L的主对角线为1无需计算,可以用主对角线作为分界线)
第65,74行:该部分与前文公式对应,每次重新计算前,需将Usum和Lsum重置为0
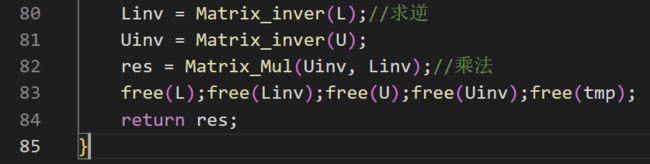
第80,81行:Matrix_inver(arr)创建的矩阵求逆函数,矩阵求逆函数可参考之前的博客:
C语言矩阵求逆(高斯法)和C语言矩阵求逆(伴随法),伴随法时间复杂度太高,推荐高斯法(代码见下方)。
第82行:Matrix_Mul(A,B)创建的矩阵乘法函数(代码见下方),为B左乘A,参考博客:C语言矩阵乘法
第83行:注意释放内存!
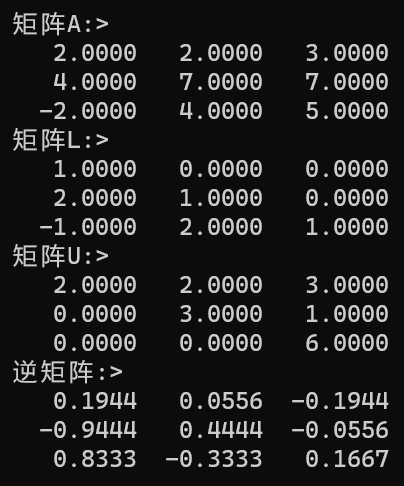
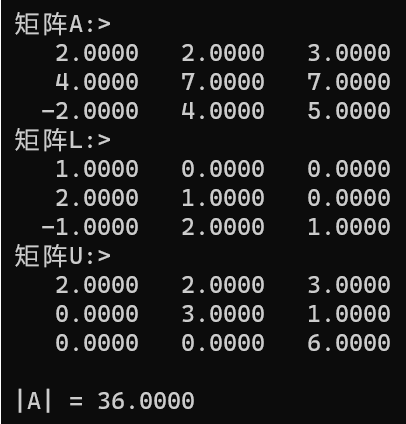
测试:
3)高斯法求逆
#include
#include
#include
#include
double** Matrix_inver(double** src)
{
//step 1
//判断指针是否为空
if (src == NULL)exit(-1);
int i, j, k, row, col, n;
double** res, ** res2,tmp;//res为增广矩阵,res为输出的逆矩阵
int count = 0;
//判断矩阵维数
row = (double)_msize(src) / (double)sizeof(double*);
col = (double)_msize(*src) / (double)sizeof(double);
if (row != col)exit(-1);
//step 2
res = (double**)malloc(sizeof(double*) * row);
res2 = (double**)malloc(sizeof(double*) * row);
n = 2 * row;
for (i = 0; i < row; i++)
{
res[i] = (double*)malloc(sizeof(double) * n);
res2[i] = (double*)malloc(sizeof(double) * col);
memset(res[i], 0, sizeof(res[0][0]) * n);//初始化
memset(res2[i], 0, sizeof(res2[0][0]) * col);
}
//step 3
//进行数据拷贝
for (i = 0; i < row; i++)
{
memcpy(res[i], src[i], sizeof(res[0][0]) * n);
}
//将增广矩阵右侧变为单位阵
for (i = 0; i < row; i++)
{
for (j = col; j < n; j++)
{
if (i == (j - row))
res[i][j] = 1.0;
}
}
for (j = 0; j < col; j++)
{
//step 4
//整理增广矩阵,选主元
count = j;
double Max = fabs(res[count][j]);//用绝对值比较
//默认第一行的数最大
//主元只选主对角线下方
for (i = j; i < row; i++)
{
if (fabs(res[i][j]) > Max)
{
count = i;
Max = fabs(res[i][j]);
}
}
if (i == j && i != count)
{
for (k = 0; k < n; k++)
{
tmp = res[count][k];
res[count][k] = res[i][k];
res[i][k] = tmp;
}
}
//step 5
//将每列其他元素化0
for (i = 0; i < row; i++)
{
if (i == j || res[i][j] == 0)continue;
double b = res[i][j] / res[j][j];
for (k = 0; k < n; k++)
{
res[i][k] += b * res[j][k] * (-1);
}
}
//阶梯处化成1
double a = 1.0 / res[j][j];
for (i = 0; i < n; i++)
{
res[j][i] *= a;
}
}
//step 6
//将逆矩阵部分拷贝到res2中
for (i = 0; i < row; i++)
{
memcpy(res2[i], res[i] + row, sizeof(res[0][0]) * row);
}
//必须释放res内存!
free(res);
return res2;
} 4)矩阵乘法
#include
#include
double** Matrix_Mul(double** arr1, double** arr2)
{
if (arr1 == NULL || arr2 == NULL)exit(-1);
int row1 = (int)_msize(arr1) / (int)sizeof(double*);
int col1 = (int)_msize(*arr1) / (int)sizeof(double);
int row2 = (int)_msize(arr2) / (int)sizeof(double*);
int col2 = (int)_msize(*arr2) / (int)sizeof(double);
if (col1 != row2)
exit(-1);//判断左列是否等于右行
double** res = (double**)malloc(sizeof(double*) * row1);
if (res == NULL)
exit(-1);
int i, j, k;
for (i = 0; i < row1; i++)
{
res[i] = (double*)malloc(sizeof(double) * col2);//创建新矩阵
}
for (i = 0; i < row1; i++)
{
for (j = 0; j < col2; j++)
{
res[i][j] = 0.0;//开辟的新矩阵未初始化,计算前需要进行初始化
for (k = 0; k < col1; k++)
{
res[i][j] += arr1[i][k] * arr2[k][j];//该部分的计算与前文一致
}
}
}
return res;
} LUP求行列式
1)代码
double Matrix_LU_Det(double** src)
{
if (src == NULL)exit(-1);
int row = (int)_msize(src) / (int)sizeof(src[0]);
int col = (int)_msize(*src) / (int)sizeof(src[0][0]);
if (row != col)exit(-1);
int i, j, k, max;
double** L, ** U, ** tmp, Lsum, Usum, p,res=1;
L = (double**)malloc(sizeof(double*) * row);
U = (double**)malloc(sizeof(double*) * row);
tmp = (double**)malloc(sizeof(double*) * row);
if (L && U)
{
for (i = 0; i < row; i++)
{
L[i] = (double*)malloc(sizeof(double) * col);
U[i] = (double*)malloc(sizeof(double) * col);
tmp[i] = (double*)malloc(sizeof(double) * col);
memset(L[i], 0, sizeof(L[0][0]) * col);//L U需初始化为0
memset(U[i], 0, sizeof(U[0][0]) * col);
memcpy(tmp[i], src[i], sizeof(src[0][0]) * col);//拷贝数据
}
}
for (i = 0; i < row; i++)
{
for (j = 0; j < row; j++)
{
if (i == j)
L[i][j] = 1;//L主对角线为1
}
}
//选主元
for (j = 0; j < col; j++)
{
max = j;
double Max = fabs(tmp[max][j]);//用绝对值比较
//默认第一行的数最大
for (i = j; i < row; i++)
{
if (fabs(tmp[i][j]) > Max)
{
max = i;
Max = fabs(tmp[i][j]);
}
}
if (i == j && i != max)
{
for (k = 0; k < col; k++)
{
p = tmp[max][k];
tmp[max][k] = tmp[i][k];
tmp[i][k] = p;
}
}
}
//计算L、U
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
if (i <= j)
{
Usum = 0;
for (k = 0; k < i; k++)
{
Usum += L[i][k] * U[k][j];
}
U[i][j] = tmp[i][j] - Usum;
}
else
{
Lsum = 0;
for (k = 0; k < j; k++)
{
Lsum += L[i][k] * U[k][j];
}
L[i][j] = (tmp[i][j] - Lsum) / U[j][j];
}
}
}
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
if (i == j)
res *= U[i][j];
}
}
free(L); free(U); free(tmp);
return res;
}2)代码讲解
LUP求行列式比较简单,没有附加的函数
注意:LUP中的选主元不用记录行变换的次数,高斯消元求行列式中的行变换需记录行变换次数
(高斯消元求行列式见C语言求行列式(高斯法))
分解完LU后,只需要将U的主对角线元素进行乘积即可,res在初始化时需为1。
测试: