XGBoost调参步骤及常见问题

XGBoost

xgboost中的基学习器除了可以是CART（gbtree）也可以是线性分类器（gblinear）

• xgboost在目标函数中显示的加上了正则化项，基学习为CART时，正则化项与树的叶子节点的数量T和叶子节点的值有关。
  正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。
  从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也是xgboost优于传统GBDT的一个特性。
  

• GB中使用Loss Function对f(x)的一阶导数计算出伪残差用于学习生成fm(x)，xgboost不仅使用到了一阶导数，还使用二阶导数。
  第t次的loss：
  
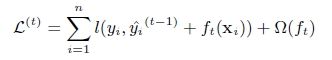
  对上式做二阶泰勒展开：g为一阶导数，h为二阶导数
  

• 上面提到CART回归树中寻找最佳分割点的衡量标准是最小化均方差，XGBoost的并行是在特征粒度上的，XGBoost预先对特征的值进行排序，然后保存为block结构
  xgboost寻找分割点的标准是最大化，lamda，gama与正则化项相关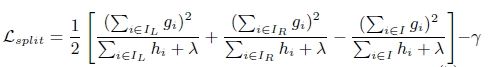
  xgboost算法的步骤和GB基本相同，都是首先初始化为一个常数，gb是根据一阶导数ri，xgboost是根据一阶导数gi和二阶导数hi，迭代生成基学习器，相加更新学习器。

• xgboost考虑了训练数据为稀疏值的情况，可以为缺失值或者指定的值指定分支的默认方向，这能大大提升算法的效率

• 列抽样。xgboost借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是xgboost异于传统gbdt的一个特性。

  XGBoost参数设置

  通用参数

  这些参数用来控制XGBoost的宏观功能。

• booster[默认gbtree]

  选择每次迭代的模型，有两种选择：
  gbtree：基于树的模型
  gbliner：线性模型

• silent[默认0]

  当这个参数值为1时，静默模式开启，不会输出任何信息。
  一般这个参数就保持默认的0，因为这样能帮我们更好地理解模型。

• nthread[默认值为最大可能的线程数]

  这个参数用来进行多线程控制，应当输入系统的核数。
  如果你希望使用CPU全部的核，那就不要输入这个参数，算法会自动检测它。

booster参数

• max_depth[默认6]

  和GBM中的参数相同，这个值为树的最大深度。
  这个值也是用来避免过拟合的。max_depth越大，模型会学到更具体更局部的样本。
  需要使用CV函数来进行调优。
  典型值：3-10

• eta[默认0.3]

  和GBM中的 learning rate 参数类似。
  通过减少每一步的权重，可以提高模型的鲁棒性。
  典型值为0.01-0.2

• base_score [ 默认0.5 ]
  所有实例的初始化预测分数，全局偏置；
  为了足够的迭代次数，改变这个值将不会有太大的影响。

• min_child_weight[默认1]
  决定最小叶子节点样本权重和。
  和GBM的 min_child_leaf 参数类似，但不完全一样。XGBoost的这个参数是最小样本权重的和，而GBM参数是最小样本总数。
  这个参数用于避免过拟合。当它的值较大时，可以避免模型学习到局部的特殊样本。
  但是如果这个值过高，会导致欠拟合。这个参数需要使用CV来调整。

• max_leaf_nodes

  树上最大的节点或叶子的数量。
  可以替代max_depth的作用。因为如果生成的是二叉树，一个深度为n的树最多生成 n 2 n^2 n2个叶子。
  如果定义了这个参数，GBM会忽略max_depth参数。

• gamma[默认0]

  在节点分裂时，只有分裂后损失函数的值下降了，才会分裂这个节点。Gamma指定了节点分裂所需的最小损失函数下降值。
  这个参数的值越大，算法越保守。这个参数的值和损失函数息息相关，所以是需要调整的。

• max_delta_step[默认0]

  这参数限制每棵树权重改变的最大步长。如果这个参数的值为0，那就意味着没有约束。如果它被赋予了某个正值，那么它会让这个算法更加保守。
  通常，这个参数不需要设置。但是当各类别的样本十分不平衡时，它对逻辑回归是很有帮助的。
  这个参数一般用不到，但是你可以挖掘出来它更多的用处。

• subsample[默认1]

  和GBM中的subsample参数一模一样。这个参数控制对于每棵树，随机采样的比例。
  减小这个参数的值，算法会更加保守，避免过拟合。但是，如果这个值设置得过小，它可能会导致欠拟合。
  典型值：0.5-1

• colsample_bytree[默认1]

  和GBM里面的max_features参数类似。用来控制每棵随机采样的列数的占比(每一列是一个特征)。
  典型值：0.5-1

• colsample_bylevel[默认1]

  用来控制树的每一级的每一次分裂，对列数的采样的占比。
  我个人一般不太用这个参数，因为subsample参数和colsample_bytree参数可以起到相同的作用。但是如果感兴趣，可以挖掘这个参数更多的用处。

• lambda[默认1]

  权重的L2正则化项。(和Ridge regression类似)。
  这个参数是用来控制XGBoost的正则化部分的。虽然大部分数据科学家很少用到这个参数，但是这个参数在减少过拟合上还是可以挖掘出更多用处的。

• alpha[默认1]

  权重的L1正则化项。(和Lasso regression类似)。
  可以应用在很高维度的情况下，使得算法的速度更快。

• scale_pos_weight[默认1]

  在各类别样本十分不平衡时，把这个参数设定为一个正值，可以使算法更快收敛

学习目标参数

这个参数用来控制理想的优化目标和每一步结果的度量方法

• objective [ default=reg:linear ]

  定义学习任务及相应的学习目标，可选的目标函数如下：

  • “reg:linear” —— 线性回归。
  • “reg:logistic”—— 逻辑回归。
  • “binary:logistic”—— 二分类的逻辑回归问题，输出为概率。
  • “binary:logitraw”—— 二分类的逻辑回归问题，输出的结果为wTx。
  • “count:poisson”—— 计数问题的poisson回归，输出结果为poisson分布。在poisson回归中，max_delta_step的缺省值为0.7。(used to safeguard optimization)
  • “multi:softmax” –让XGBoost采用softmax目标函数处理多分类问题，同时需要设置参数num_class（类别个数）
  • “multi:softprob” –和softmax一样，但是输出的是ndata * nclass的向量，可以将该向量reshape成ndata行nclass列的矩阵。没行数据表示样本所属于每个类别的概率。
  • “rank:pairwise” –set XGBoost to do ranking task by minimizing the pairwise loss

• eval_metric [ default according to objective ]
  对于回归问题，默认值是rmse，对于分类问题，默认值是error。

  • rmse 均方根误差
  • mae 平均绝对误差
  • logloss 负对数似然函数值
  • error 二分类错误率(阈值为0.5)
  • merror 多分类错误率
  • mlogloss 多分类logloss损失函数
  • auc 曲线下面积

• seed [ default=0 ]
  随机数的种子。缺省值为0

from sklearn.model_selection import train_test_split

train_x, test_x, train_y, test_y = train_test_split(feature_matrix, labels, random_state=0)

import xgboost as xgb
dtrain=xgb.DMatrix(train_x,label=train_y)
dtest=xgb.DMatrix(test_x)

params={    'booster': 'gbtree',            
    'objective': 'multi:softmax',  # 多分类的问题
    'num_class': 10,               # 类别数，与 multisoftmax 并用
    'gamma': 0.1,                  # 用于控制是否后剪枝的参数,越大越保守，一般0.1、0.2这样子。
    'max_depth': 12,               # 构建树的深度，越大越容易过拟合
    'lambda': 2,                   # 控制模型复杂度的权重值的L2正则化项参数，参数越大，模型越不容易过拟合。
    'subsample': 0.7,              # 随机采样训练样本
    'colsample_bytree': 0.7,       # 生成树时进行的列采样
    'min_child_weight': 3,
    'silent': 1,                   # 设置成1则没有运行信息输出，最好是设置为0.
    'eta': 0.1,                  # 如同学习率
    'seed': 1000,
    'nthread': 10                 # cpu 线程数，默认值为最大可能的线程数
}

watchlist = [(dtrain,'train')]

bst=xgb.train(params,dtrain,num_boost_round=100,evals=watchlist)

y_pred=bst.predict(dtest)

y_pred_binary = (ypred >= 0.5)*1

from sklearn import metrics
print 'AUC: %.4f' % metrics.roc_auc_score(test_y,y_pred)
print 'ACC: %.4f' % metrics.accuracy_score(test_y,y_pred_binary)
print 'Recall: %.4f' % metrics.recall_score(test_y,y_pred_binary)
print 'F1-score: %.4f' %metrics.f1_score(test_y,y_pred_binary)
print 'Precesion: %.4f' %metrics.precision_score(test_y,y_pred_binary)
metrics.confusion_matrix(test_y,y_pred_binary)

参数调优的一般方法

我们会使用和GBM中相似的方法。需要进行如下步骤：

• 选择较高的学习速率(learning rate)。一般情况下，学习速率的值为0.1。但是，对于不同的问题，理想的学习速率有时候会在0.05到0.3之间波动。选择对应于此学习速率的理想决策树数量。XGBoost有一个很有用的函数“cv”，这个函数可以在每一次迭代中使用交叉验证，并返回理想的决策树数量。
• 对于给定的学习速率和决策树数量，进行决策树特定参数调优(max_depth, min_child_weight, gamma, subsample, colsample_bytree)。在确定一棵树的过程中，我们可以选择不同的参数。
• xgboost的正则化参数的调优。(lambda, alpha)。这些参数可以降低模型的复杂度，从而提高模型的表现。
• 降低学习速率，确定理想参数。

import xgboost as xgb

data_train = xgb.DMatrix('agaricus_train.txt')
data_test = xgb.DMatrix('agaricus_test.txt')
print (data_train)
print (type(data_train))

# 设置参数
param = {'max_depth': 3, 'eta': 1, 'silent': 1, 'objective': 'binary:logistic'} 

# 可以显示每一颗树添加后的误差
watchlist = [(data_test, 'eval'), (data_train, 'train')]
n_round = 50
bst = xgb.train(param, data_train, num_boost_round=n_round, evals=watchlist, obj=log_reg, feval=error_rate)

# 计算错误率
y_hat = bst.predict(data_test)
y = data_test.get_label()
print(y_hat)
print(y)

XGBoost常见问题

xgboost 什么场景不适用

数据量很大以及特征比较多时太耗内存，太慢了，比如寻找最优特征分裂点时需要遍历所有特征去计算(虽然做了预排序和并行处理) ,但它还是很慢和很耗内存，需要读取所有数据到内存中才好做特征分裂。

GDBT 和Xgboost 的区别？

好的地方： 二阶泰勒展开，节点分数惩罚正则，增益计算不同，gbdt 是gini，xgb 是优化推导公式

• 传统的GBDT以CART作为基分类器，XGboost 还支持线性分类器，这时候xgboost 相当于带L1 和L2 正则化项的逻辑斯蒂回归(分类问题) 或者线性回归。

• 传统的GBDT在优化时只用到了一阶导数信息，xgboost 则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数，xgboost 还支持自定义代价函数，只要函数可一阶和二阶求导。

• Xgboost 在代价函数中加入了正则项，用于控制模型的复杂度，正则项里包含了 树的叶子节点个数，每个叶子节点上输出的score 的L2 模的平方和。从Bias -variance tradeoff 角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也就是xgboost 优于传统CBDT的一个特性。

• Shrinkage ,相当于学习速率(xgboost 中的eta) .Xgboost 在进行完一次迭代后，会将叶子节点上权重·乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间，实际应用中，一般把eta 设置的小一点，然后迭代次数设置的大一点。

• 列抽样，： xgboost 借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是xgboost 异于传统gdbt 的一个特性。

• 缺失值的处理，对特征的值有缺失的样本，xgboost 可以自动学习出它分裂的方向。

• xgboost 支持并行，不是在trees 粒度的并行，而是在特征粒度上的，决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点) ,xgboost 在训练之前，预先对数据进行了排序，然后保存了block 结构，后面的迭代中重复使用了这个结构，大大减少了计算量。在进行节点分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算可以开多线程进行。

• 可并行的近似直方图算法，树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有节能的分割点，当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost 还提出了一种可并行的近似直方图算法，用于高效的生成候选的分割点。

XGBoost 和lgb 的区别

是对GBDT 方法的不同实现，针对同一目标，做了不同的优化处理。

它们在基础逻辑上并没有啥不同，限定max_tree或者max_iterations，之后算法从0 棵树开始跑，每一轮根据上一轮的残差增加一颗决策树，在每一次增加决策树的时候选择当前最优结构，而在生成当前决策树的过程中，采用了不同的优化方案。

• XGBoost 使用基于预排序的决策树算法，每遍历一个特征需要计算一次特征增益，时间复杂度为Q(datafeature).

lgb 使用基于直方图的决策树算法，直方图的优化算法只需要计算k 次，时间复杂度为O(kfeature)

• XGBoost 按照层生长的决策树生成，LGb采用带有深度限制的叶子节点算法，在分裂次数相同的情况下，leaf-wise 可以降低更多的误差，得到更好的精度，leaf-wise 的缺点在于会产生较深的决策树，产生过拟合。

• 支持类别特征，不需要进行独热编码处理。

• 优化了特征并行和数据并行算法，除此之外还添加了投票并行方案。

• 采用基于梯度的单边采用来保持数据分布，减少模型因数据分布发生变化而造成的模型精度下降。

• 特征捆绑转化为图着色问题，减少特征数量。

XGBoost分裂终止条件

• 当引入的分裂带来的增益小于一个阀值的时候，我们可以剪掉这个分裂，所以并不是每一次分裂loss function整体都会增加的，有点预剪枝的意思（其实我这里有点疑问的，一般后剪枝效果比预剪枝要好点吧，只不过复杂麻烦些，这里大神请指教，为啥这里使用的是预剪枝的思想，当然Xgboost支持后剪枝），阈值参数为γγ 正则项里叶子节点数T的系数（大神请确认下）；

• 当树达到最大深度时则停止建立决策树，设置一个超参数max_depth，这个好理解吧，树太深很容易出现的情况学习局部样本，过拟合；

• 当样本权重和小于设定阈值时则停止建树，这个解释一下，涉及到一个超参数-最小的样本权重和min_child_weight，和GBM的 min_child_leaf 参数类似，但不完全一样，大意就是一个叶子节点样本太少了，也终止同样是过拟合；