【吴恩达机器学习笔记】十、支持向量机

✍个人博客：https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
专栏定位：为学习吴恩达机器学习视频的同学提供的随堂笔记。
专栏简介：在这个专栏，我将整理吴恩达机器学习视频的所有内容的笔记，方便大家参考学习。
专栏地址：https://blog.csdn.net/Newin2020/article/details/128125806
视频地址：吴恩达机器学习系列课程
❤️如果有收获的话，欢迎点赞收藏，您的支持就是我创作的最大动力

十、支持向量机

1. 优化目标

在讲支持向量机之前，我们先从逻辑回归开始渡过到支持向量机。

上面图中粉红色的那条线就是支持向量机的曲线，和逻辑回归很相似，代价函数都分两个部分构成。

支持向量机（Support vector machine）- SVM

支持向量机和逻辑回归不相同的主要在两个地方：

• 支持向量机代价函数没有m，因为就算没有m对最终θ的结果都没有影响，上面图左下就举了个例子。
• 逻辑回归的代价函数分两个部分，像上面一样我们分成A和B两部分，逻辑回归对于λ较为看重，因为它决定了A所占的权重。支持向量机没有λ，而是用另一种方式表示，拿C来代替，它会放在A上面，决定着B的权重。

支持向量机还有一个地方与逻辑回归不同的是，逻辑回归假设函数输出的是概率，而支持向量机假设函数输出的结果是直接预测了y是1还是0。

2. 直观上对大间隔的理解

来看看支持向量机代价函数肚饿图像，会发现：

• 当y=1时，我们希望θ^Tx ≥ 1才能得到z为0，而不是单纯的只需其≥0即可。
• 当y=1时，我们希望θ^Tx 小于等于 -1才能得到z为0，而不是单纯的只需其≤0即可。

而这个-1到1的间隔，我们称为安全间隔，如果我们想要让代价函数第一部分的式子为0，那么就要满足上面y=1或y=0的要求。接下来我们来看看，支持向量机的决策边界会呈现什么效果。

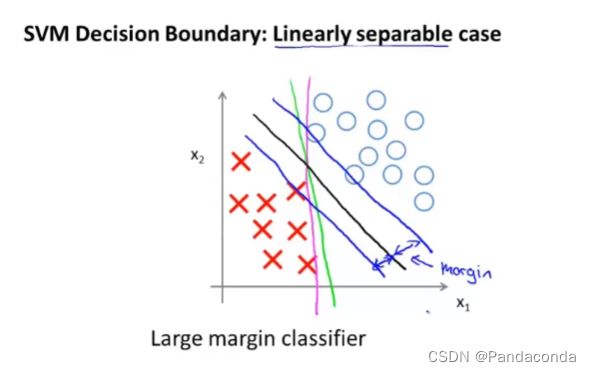
图中黑色的那条线就是支持向量机分类的结果，可以看出它和绿色与紫色的划分线不同，它与样本之间有一定的间距，所以我们有时候也会称SVM为大间距分类器（Large margin classifier）。

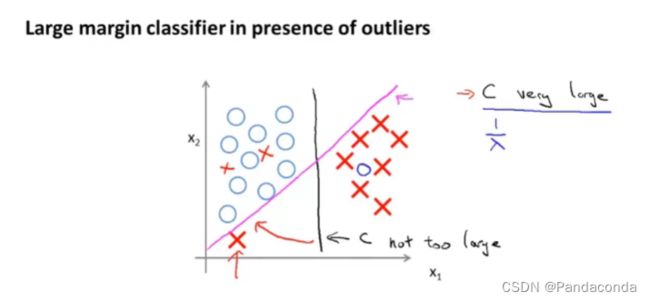
但是，如果我们将C设置的特别大的话，就会出下下面这种情况：

如上图紫色划分线，如果C太大，支持向量机对于异常值就会特别敏感，导致变化特别大，而如果C设置的很小，支持向量机对于异常值就会几乎忽略不计，就还会是我们上图的黑线那样。

3. 核函数

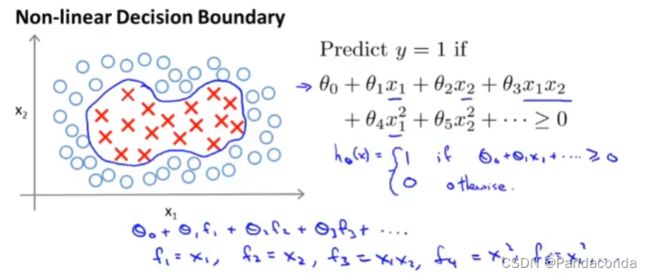
首先，我们来看一个复杂的非线性函数：

可以发现，这个函数中包含了一些复合的特征，那对于这种非常复杂的非线性边界，是否有更好的特征去代替这些f1、f2、f3等等呢。

核函数（Kernel）

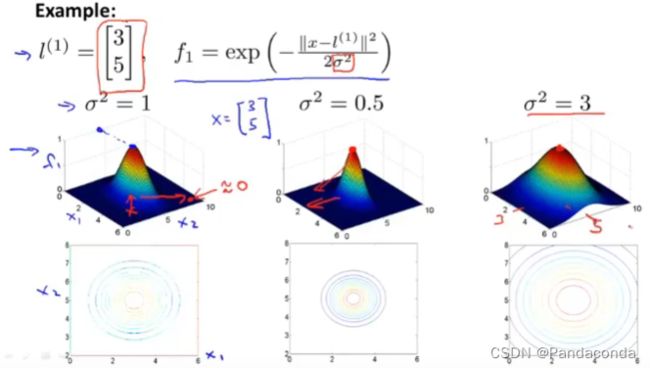
假设我们通过给定一个x案例，并且选出三个标记（landmark），然后定义特征f为一个相似度函数，这里用到的函数就是高斯核函数（Gaussian kernels），是核函数中的一种。

接下来，我们来看看新特征内的具体计算。

可以发现，如果标记离给出的案例x点很近时，(x_j-l_j)²会几乎为0，那么e函数会接近于1，所以特征f就会接近于1；同样如果标记离给出的案例x点很远时，特征f就会接近于0，我们再来看一个具体的例子。

上图中我们对σ的值进行了改变，σ是高斯核函数的参数，当σ越小时，可以发现当x离l越远时，下降的比σ原先下降的更快，同理当σ越大时，则下降的会更慢。

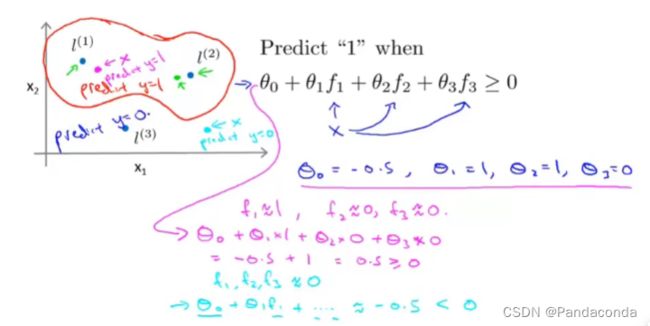
现在我们再将这些新的特征代替原来函数中的特征，可以得到下面这个例子：

我们可以假设θ的值并取一些x进行计算，发现靠近l⁽¹⁾和l⁽²⁾时，y都被预测为1；远离l⁽¹⁾和l⁽²⁾时，y都被预测为0，从而利用核函数得到一个非线性的决策边界。

大概解释完上面核函数的流程后，我们来看看核函数中的标记l是如何选择的。

我们得到标记l的方式很简单，可以直接将训练集样本的位置作为标记的位置即可。

接下来，我们来看一下核函数的参数。

• C（作用类似于正则化中的1/λ）

  • 如果C很大，则对应着低偏差，高方差即过拟合问题。
  • 如果C很小，则对应这高偏差，低方差即欠拟合问题。

• σ²

  • 如果σ²很大，则对应着高偏差，低方差即欠拟合问题。
  • 如果σ²很小，则对应着低偏差，高方差即过拟合问题。

最后，我们再来对支持向量机中的核函数使用过程进行一个小回顾。

4. 使用SVM

这节课我们来讨论一下，使用SVM时的一些注意事项。

首先，第一个建议是不要尝试去写一些已经有人写好的数据包，直接去调用即可（例如liblinear,libsvm等）。

其次，你要注意的是，有两个地方是需要你人为完成的：

• 选择一个参数C。
• 选择一个核函数（相似函数）。
  • 可以是线性的核函数即不使用核函数，这种一般是在特征很多，训练集很少容易过拟合的情况下使用。
  • 可以是高斯核函数，这种一般是在特征很少，训练集比较多的情况下使用。

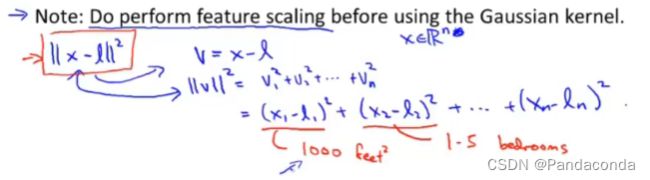
如果你选择了高斯核函数，那么在训练时若你的x特征之间差别特别大，需要进行等比例缩放。

除上述的两个函数之外，还有其他的核函数，但有效的核函数都要满足默塞尔定理（Mercer’s Theorem），即确保所有的SVM软件包能够利用大类的优化方法并从而迅速得到参数θ。

• 多项式核函数
  • 通过改变参数增加一些参数来调整效果，并且x和l一般是非负的以保证内积大于0，如下图中的一些例子。
• 其他复杂函数
  • 字符串核函数（String kernel），卡方核函数（chi-square kernel），直方相交核函数（histogram intersection kernel）等等。

再者，我们来讨论讨论SVM一对多的分类情况，这与逻辑回归中的一对多的方法一样，都是分别训练各个类别的分类器，预测时选取分类器得分最高的即可。

最后，我们来讨论一下逻辑回归和支持向量机何时使用较好。

• 如果特征比训练集多很多，则一般用逻辑回归或不带核函数的SVM。
• 如果特征很少，训练集数量适中，则一般用高斯核函数。
• 如果特征很少且训练集数量很大很大，则一般用逻辑回归或不带核函数的SVM。

神经网络不管对应哪个情形效果都不错，但是缺点是训练速度会比较慢。