神经网络架构搜索——可微分搜索（PC-DARTS）

华为发表在ICLR 2020上的NAS工作，针对现有DARTS模型训练时需要 Large memory and computing 问题，提出了 Partial Channel Connection 和 Edge Normalization 的技术，在搜索过程中更快更好。

• aper: PC-DARTS: Partial Channel Connections for Memory-Efficient Differentiable Architecture Search
• Code: https://github.com/yuhuixu1993/PC-DARTS

动机

接着上面的P-DARTS来看，尽管上面可以在17 cells情况下单卡完成搜索，但妥协牺牲的是operation的数量，这明显不是个优秀的方案，故此文 Partially-Connected DARTS，致力于大规模节省计算量和memory，从而进行快速且大batchsize的搜索。

贡献点

• 设计了基于channel的sampling机制，故每次只有小部分1/K channel的node来进行operation search，减少了(K-1)/K 的memory，故batchsize可增大为K倍。

• 为了解决上述channel采样导致的不稳定性，提出了 边缘正规化(edge normalization)，在搜索时通过学习edge-level超参来减少不确定性。

方法

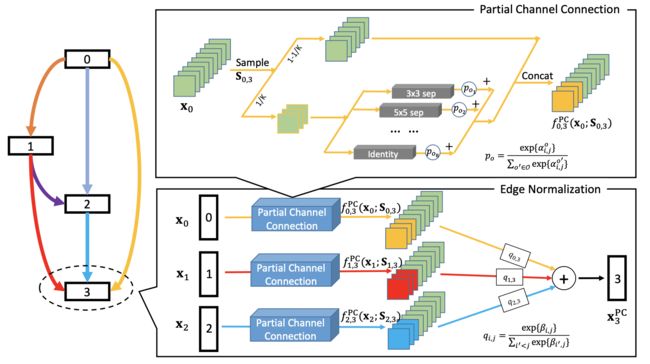
部分通道连接(Partial Channel Connection)

如上图的上半部分，在所有的通道数K里随机采样 1/K 出来，进行 operation search，然后operation 混合后的结果与剩下的 (K-1)/K 通道数进行 concat，公式表示如下：

$$f_{i,j}^{\mathrm{P}\mathrm{C}}\left({\mathbf{x}}_i;{\mathbf{S}}_{i,j}\right)=\sum _{o\in \mathcal{O}}\frac{\exp \left\{{\alpha }_{i,j}^o\right\}}{{\sum }_{o^{\prime }\in \mathcal{O}}\exp \left\{{\alpha }_{i,j}^{o^{\prime }}\right\}}\cdot o\left({\mathbf{S}}_{i,j}\ast {\mathbf{x}}_i\right)+\left(1-{\mathbf{S}}_{i,j}\right)\ast {\mathbf{x}}_i$$

上述的“部分通道连接”操作会带来一些正副作用：

• 正作用：能减少operations选择时的biases，弱化无参的子操作（Pooling, Skip-Connect）的作用。文中3.3节有这么一句话：当proxy dataset非常难时（即ImageNet），往往一开始都会累积很大权重在weight-free operation，故制约了其在ImageNet上直接搜索的性能。
• 副作用：由于网络架构在不同iterations优化是基于随机采样的channels，故最优的edge连通性将会不稳定。

class MixedOp(nn.Module):

  def __init__(self, C, stride):
    super(MixedOp, self).__init__()
    self._ops = nn.ModuleList()
    self.mp = nn.MaxPool2d(2,2)

    for primitive in PRIMITIVES:
      op = OPS[primitive](C //4, stride, False)
      if 'pool' in primitive:
        op = nn.Sequential(op, nn.BatchNorm2d(C //4, affine=False))
      self._ops.append(op)

  def forward(self, x, weights):
    #channel proportion k=4（实验证明1/4性能最佳）
    dim_2 = x.shape[1]
    xtemp = x[ : , :  dim_2//4, :, :] # channel 0到1/4的输入
    xtemp2 = x[ : ,  dim_2//4:, :, :] # channel 1/4到1的输入
    temp1 = sum(w * op(xtemp) for w, op in zip(weights, self._ops)) # 仅1/4数据参与ops运算
    #reduction cell 需要在concat之前添加pooling操作
    if temp1.shape[2] == x.shape[2]:
      ans = torch.cat([temp1,xtemp2],dim=1)
    else:
      ans = torch.cat([temp1,self.mp(xtemp2)], dim=1)
    ans = channel_shuffle(ans,4) # 一个cell完成后对channel进行随机打散，为下个cell做采样准备
    #ans = torch.cat([ans[ : ,  dim_2//4:, :, :],ans[ : , :  dim_2//4, :, :]],dim=1)
    #except channe shuffle, channel shift also works
    return ans

def channel_shuffle(x, groups):
    batchsize, num_channels, height, width = x.data.size()

    channels_per_group = num_channels // groups
    
    # reshape [batchsize, num_channels, height, width] 
    # -> [batchsize, groups,channels_per_group, height, width]
    x = x.view(batchsize, groups, 
        channels_per_group, height, width)
		# 打乱channel的操作(借助transpose后数据块的stride发生变化，然后将其连续化)
    # 参考：https://www.cnblogs.com/aoru45/p/10974508.html
    x = torch.transpose(x, 1, 2).contiguous()

    # flatten
    x = x.view(batchsize, -1, height, width)

    return x

边缘正规化(Edge Normalization)

为了克服部分通道连接这个副作用，提出边缘正规化（见上图的下半部分），即把多个PC后的node输入softmax权值叠加，类attention机制

$${\mathbf{x}}_j^{\mathrm{P}\mathrm{C}}=\sum _{o\in \mathcal{O}}\frac{\exp \left\{{\alpha }_{i,j}^o\right\}}{{\sum }_{o^{\prime }\in \mathcal{O}}\exp \left\{{\alpha }_{i,j}^{o^{\prime }}\right\}}\cdot o\left({\mathbf{S}}_{i,j}\ast {\mathbf{x}}_i\right)+\left(1-{\mathbf{S}}_{i,j}\right)\ast {\mathbf{x}}_i$$

$${\mathbf{x}}_j^{\mathrm{P}\mathrm{C}}=\sum _{i<j}\frac{\exp \left\{{\beta }_{i,j}\right\}}{{\sum }_{i^{\prime }<j}\exp \left\{{\beta }_{i^{\prime },j}\right\}}\cdot f_{i,j}\left({\mathbf{x}}_i\right)$$

由于edge 超参 ${\beta }_{i,j}$ 在训练阶段是共享的，故学习到的网络更少依赖于不同iterations间的采样到的channels，使得网络搜索过程更稳定。当网络搜索完毕，node间的operation选择由operation-level和edge-level的参数相乘后共同决定。

weights_normal = [F.softmax(alpha, dim=-1) for alpha in alpha_normal]
weights_reduce = [F.softmax(alpha, dim=-1) for alpha in alpha_reduce]
weights_edge_normal = [F.softmax(beta, dim=0) for beta in beta_normal]
weights_edge_reduce = [F.softmax(beta, dim=0) for beta in beta_reduce]


def parse(alpha, beta, k):
		...  
    for edges, w in zip(alpha, beta):
        edge_max, primitive_indices = torch.topk((w.view(-1, 1) * edges)[:, :-1], 1) # ignore 'none'
    ...

实验结果

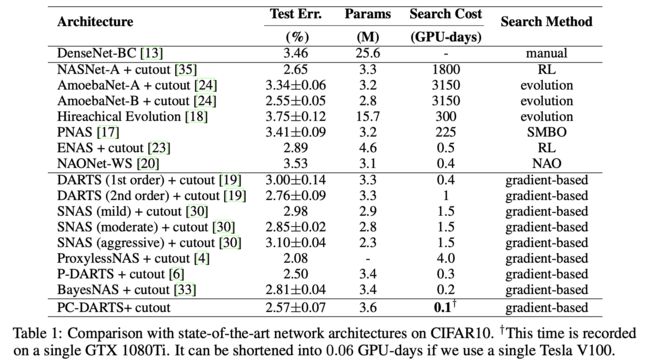
CIFAR-10

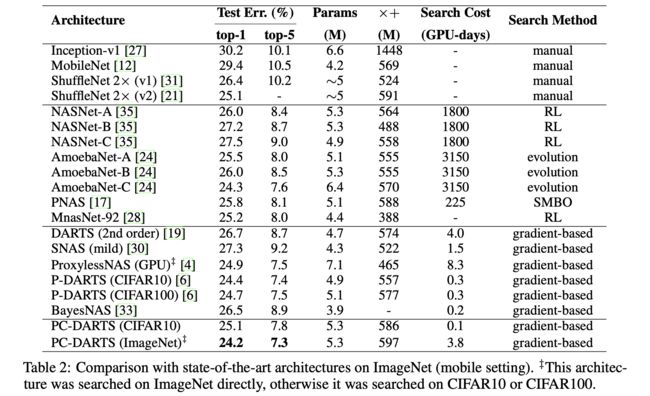
ImageNet

消融实验

参考

[1] Yuhui Xu et al. ,PC-DARTS: Partial Channel Connections for Memory-Efficient Differentiable Architecture Search

[2] https://zhuanlan.zhihu.com/p/73740783

---