Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

ViT将transformer从NLP领域应用到了视觉领域，但是它仅做了分类工作，Swin transformer的提出彻底将Transformer应用到了视觉领域的各个细分领域中，使得transformer成为了视觉领域的一个骨干网络。

摘要

这篇论文提出了一种新的视觉Transformer，称为Swin Transformer，它可以作为计算机视觉领域的一个通用骨干网络。将Transformer直接从NLP领域迁移到视觉领域存在两个挑战，一个是尺度问题，另外一个是图像像素过多（如果我们以像素为单位，那么序列长度就会过长）。为了解决这些问题，我们提出了hierarchical Transformer，它的特征通过移动窗口计算得到。移动窗口不仅能提高效率，还能使得相邻窗口间存在交互，变相达到了全局建模的能力。层级式的设计不仅可以提供各个尺度的特征信息，同时由于自注意力是在小窗口之内计算得到，它的计算复杂度随着图像大小而线性变化（相比于平方级变化）。由于Swin Transformer也像卷积神经网络一样拥有多尺度特征，因此它很容易应用到下游任务里，例如图像分类（作者在ImageNet-1K上进行了实验，top-1 准确率达到了87.3），密集预测型任务例如目标检测（在COCO test-dev上实现了587 box AP以及 51.1 mask AP），物体分割任务（在ADE20K val上实现了53.5 mIoU）。基于Transformer的模型在视觉领域是非常有潜力的。对于MLP结构，移动窗口方法也能提升。

引言

作者首先介绍了Vision Transformer，将它放在图1右部进行了对比。Vision Transformer将图片打包成patch（token），ViT里面使用的patch size是$16\times 16$的，因此图中的$16\times$意味着16倍的下采样率。每一层的Transformer block看到的token的尺寸都是16倍的下采样率。虽然可以通过全局的自注意力操作达到全局的建模能力，但是对多尺寸特征的把握会弱一些，但是对于下游的视觉任务（例如检测和分割），多尺寸特征是至关重要的。因此作者说，ViT处理的特征都是单一尺寸、low resolution的，这就是说，自始至终都处理16倍下采样率过后的特征，所以它可能就不适合处理这种密集预测型的任务。同时对ViT而言，它的自注意力始终在最大的窗口上进行（始终都是在整图上进行），所以它是一个全局建模，因此复杂度根据图像尺寸进行平方倍的增长。对于检测和分割来说（这种任务采用的图像分辨率通常很大），计算复杂度过大，所以基于这些挑战，作者提出了Swin Transformer。

Swin Transformer借鉴了很多卷积神经网络的设计理念和先验知识，比如为了减少序列长度，降低计算复杂度，Swin Transformer采取了在小窗口内计算自注意力，而不是像ViT一样在整图上计算自注意力，这样只要窗口大小固定，自注意力的计算复杂度就是固定的，这样整张图的计算复杂度就会和图片的大小成线性增长关系。这个就算是利用了卷积神经网络里的Locality的Inductive bias，就是利用了局部性的先验知识（同一个物体的不同部位，或者语义相近的不同物体，会大概率出现在相邻的地方），所以即使我们在Local（小范围窗口）去计算自注意力，也是差不多够用的。全局计算自注意力对于视觉任务来说其实是浪费资源的。

另外一个挑战是如何生成多尺寸特征，卷积神经网络有多尺寸特征主要是因为有Pooling（池化）操作，池化操作可以增大每个卷积核的感受野，从而使得每次池化过后的特征获取不同尺度的信息。Swin Transformer也提出了一个类似池化的操作，叫做patch merging，这就是将相邻的小patch合并成一个大patch，这样合并成的大patch就可以看到之前四个小patch所看到的内容，它的感受野就增大了，同时它也能抓住多尺度的特征。如图一左部分所示，Swin Transformer刚开始下采样率是四倍，然后变成八倍、十六倍（最开始的patch是$4\times 4$大小），在我们获取了多尺度信息后，我们可以将多尺度信息输入给一个FPN，此时我们可以进行检测过程，同样我们可以将多尺度信息交给UNET进行分割工作。这就是作者反复强调的，Swin Transformer可以作为一个通用的骨干网络。

Swin Transformer的一个关键的要素就是移动窗口设计，具体内容如图二所示：

图二中说，如果在Transformer的第L层，我们将输入分成小窗口，那就可以有效降低序列长度，从而减少计算复杂度，右方的灰色小patch是最基本的元素单元（$4\times 4$的patch）。每个红色的框是一个中型的计算单元，也就是一个窗口，在Swin Transformer中，每个红色窗口默认有49个小patch（图中仅是个示意图）。

如果我们将整体的layer l作为特征图（即左侧的四个大红色方块），shift的操作就是往右下角的方向整体移动了两个patch。也就变成了右图中蓝色的部分：

然后我们在新的特征图里面再次分四方格：

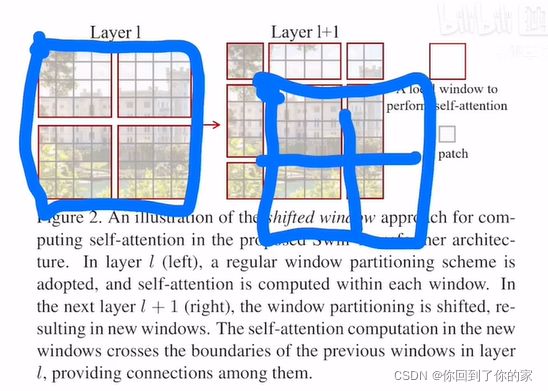
最后shift操作完成后，我们就有图一中间部分这些窗口了，这样做的好处是窗口与窗口之间现在可以进行互动。因为如果我们按照原来的方式，窗口之间是不重叠的，此时自注意力操作每次都在小窗口内进行：

那么这个窗口内的patch就无法注意到别的窗口内的patch信息：

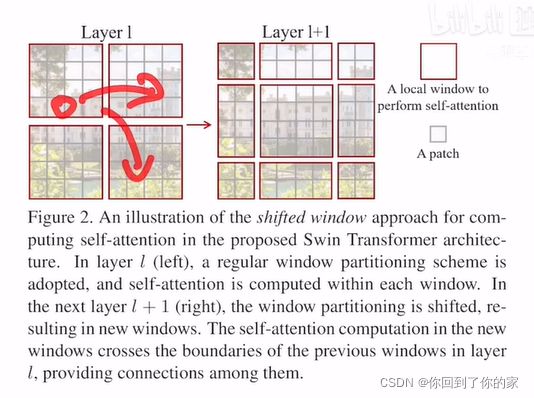
这无法达到使用Transformer的初衷，因为Transformer的初衷就是更好地理解上下文，如果各个窗口不重叠，那么自注意力就变成了孤立自注意力。当我们加上shift操作之后，以下面的patch为例：

此时这个patch可以和新的窗口内的patch进行交互：

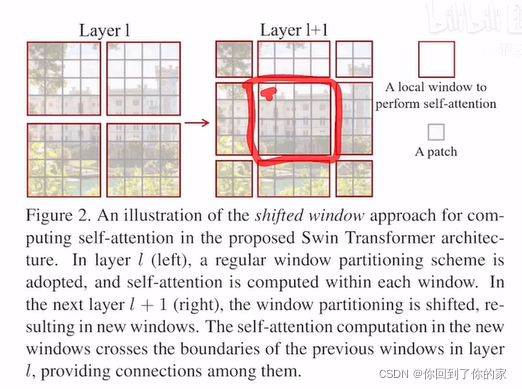
这就是作者说的cross-window connection，窗口和窗口之间的交互。再加上patch merging，合并到Transformer最后几层时，每个patch本身的感受野就已经很大了，可以看到图片的大部分了。再加上移动窗口的操作，现在窗口内的局部注意力其实也就变相的等于是一个全局的自注意力操作了。这样既省内存效果也好。

方法

前向过程介绍

首先看一下模型总览图：

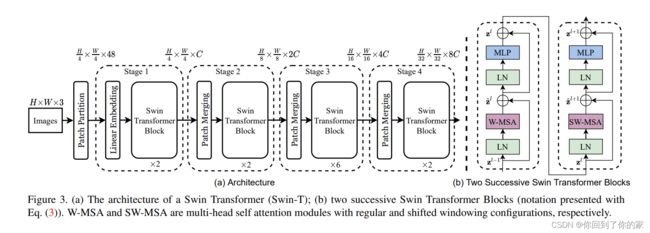
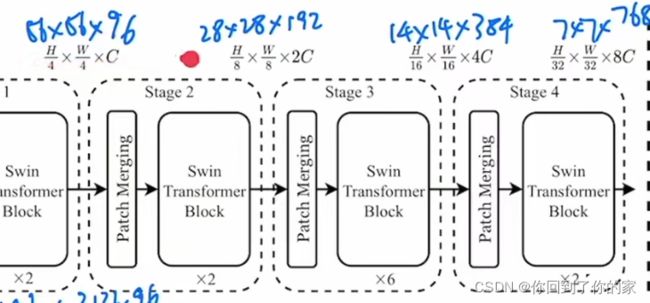
假设我们有一个$224\times 224\times 3$的输入图片，第一步就是将图片转化为patch，Swin Transformer中patch size是$4\times 4$，在经过Patch Partitaion后，图片的尺寸是$56\times 56\times 48$。

打包好了patch后，接下来我们进行Linear Embedding，将向量维度变成一个我们预先设置好的值（Transformer能够接收的值）。在Swin Transformer论文中，这个值为$C$，图中这个值为96，因此现在图片变成了$56\times 56\times 96$。前面的$56\times 56$会拉直变成序列长度3136，后面的96就变成了每一个token的向量维度。patch partition和linear embedding就相当于ViT里面Patch Projection那一步操作。

现在3136的序列长度过长，因此Transformer引入了基于窗口的自注意力计算，每个窗口按照默认都只有49个patch，序列长度只有49。这里的Swin Transformer Block是基于窗口来计算自注意力的。（暂时认为它是黑盒，仅关心输入输入维度，对Transformer来说，输入输出的尺寸是相同的）。因此输出是$56\times 56\times 96$，如下图所示：

接下来我们想要多尺寸信息，此时我们要构建一个层级式的transformer，也就是说我们需要类似卷积神经网络中的池化操作。本文中作者就使用了patch merging。

举如下例子：

假设我们有如下一个$H\times W\times C$的张量，那么patch merging就是将临近的小patch合并成一个大patch，这样就可以起到下采样一个特征图的效果了。

这里下采样率设置为2倍，这意味着每隔两个点采样一个点，因此采样点如下所示（这里 1 2 3 4指代序号，而不是具体的值）：

经过了每隔一个点取一个样之后，之前的一个张量就变成了四个张量：

现在我们将这四个张量在c这个维度上拼接起来：

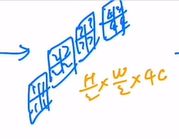
此时张量的维度变成了$\frac{H}{2}\times \frac{W}{2}\times 4c$，通过这种操作，我们将原来的大张量变小，就和卷积神经网络中的池化操作一样。同时为了和卷积神经网络（VGG、Resnet等池化操作后通道数翻倍，而不是变成四倍）统一，下一步在c这个维度上使用$1\times 1$的卷积将通道数降为2c。通过这一系列操作，我们将一个$H\times W\times c$的张量变成了$\frac{H}{2}\times \frac{W}{2}\times 2c$的张量，此时和卷积神经网络对等了起来，这整个过程就是patch merging。

回到总览图，我们观察二阶段：

此时输出大小从$56\times 56\times 96$变成了$28\times 28\times 192$，再经过Transformer Block后，尺寸不变。

第三阶段和第四阶段同理。

为了和卷积神经网络保持一致，Swin Transformer并没有像ViT一样使用CLS token。它在得到了最后的$7\times 7\times 768$的特征图后，使用了global average pooling操作，直接将$7\times 7$取平均拉直变成了1：

这样就完成了整个分类网络的前向过程。

基于移动窗口的自注意力操作

全局的自注意力计算会导致平方倍的复杂度，当我们遇到尺寸很大的图片或者进行密集预测型任务时，开销过高。因此作者提出了基于窗口进行自注意力操作。接下来通过一个例子来说明窗口是怎么划分的，原图会被平均分成一些没有重叠的窗口，以第一层之前的输入为例，现在的尺寸是$56\times 56\times 96$，然后我们将它切成一些不重叠的方格：

每个橘黄色的方格都是一个窗口，但是这个窗口并不是最小的计算单元，最小的计算单元还是之前的patch，这也就是说，每个小窗口内还有$M\times M$个patch，在Swin Transformer中，一般这个m默认为7，也就是说，一个橘黄色的小方格内有49个patch，现在所有自注意力操作都是在这些小窗口内进行的，序列长度永远都是49。对于原来大的整体特征图，每条边都有56/7=8个窗口，一共64个窗口。我们在这64个窗口内分别计算自注意力，Swin Transformer论文中大概估计了基于窗口的自注意力比全局自注意力节省多少计算复杂度，对应如下两个公式：

$$\begin{gathered} \Omega (\text{MSA})=4hw{C}^2+2(hw{)}^{2}C \\ \Omega (\text{W-MSA})=4hw{C}^2+2M^{2}hwC \end{gathered}$$

第一个公式对应于标准的多头自注意力计算复杂度。每个图片大概有$h\times w$个patch（对应于刚才的例子是56），C是特征的维度。第二个公式对应于基于窗口的自注意力计算复杂度，这里的M就是刚才的7，这是一个窗口的每条边上现在有多少个patch。

接下来介绍下上面的公式如何推算得到，以标准的多头自注意力为例。

首先我们将原来的向量变为q、k、v三个向量：

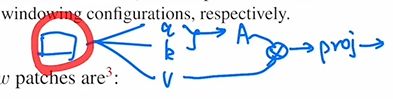
得到了query和q之后，我们进行相乘得到attention（自注意力矩阵）：

得到自注意力矩阵后，我们将它和value做一次乘法，这相当于进行了一次加权。因为是多头自注意力，所以最后还有一个projection layer。这个投射层会把向量的维度投射到我们想要的维度。

现在假如我们给这些向量都加上它们该有的维度：

也就是说最开始的输入是$hw\times c$，接下来我们用它去乘$c\times c$的系数矩阵。这时我们得到的输出是$hw\times c$。所以每一个计算复杂度都是$hw{C}^2$，因为我们有三次操作，所以是三倍的$hw\times C^2$。

接下来计算自注意力，

结论

本文提出了Swin Transformer，这是一个层级式的Transformer，并且它的计算复杂度是跟输入图像的大小呈线性增长的。Swin Transformer在COCO和ADE20K上的效果都非常好，远远超过了之前的最好的方法。

作者认为，在Swin Transformer中，最关键的一个贡献是基于Shifted Window的自注意力机制，这对许多下游的视觉任务（密集预测型）的任务是非常有帮助的。