汉诺塔问题:递归与非递归实现
目录
1.汉诺塔问题是什么?
2.汉诺塔问题分析
3.代码实现:
递归实现:
非递归实现(利用堆栈):
1.定义栈类:
2.定义问题类:
3.主函数:
方式1:利用数组充当堆栈
方式2:利用单向队列充当堆栈:
非递归代码思路讲解:
利用递归树深层理解递归:
1.汉诺塔问题是什么?
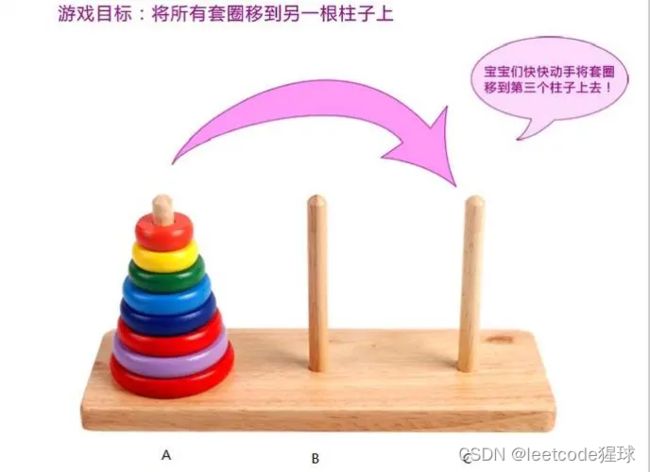
相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
图示如下:
2.汉诺塔问题分析
分析:对于这样一个问题,任何人都不可能直接写出移动盘子的每一步,但我们可以利用下面的方法来解决。设移动盘子数为n,为了将这n个盘子从A杆移动到C杆,可以做以下三步:
(1)以C盘为中介,从A杆将1至n-1号盘移至B杆;
(2)将A杆中剩下的第n号盘移至C杆;
(3)以A杆为中介;从B杆将1至n-1号盘移至C杆
这样问题解决了,但实际操作中,只有第二步可直接完成,而第一、三步又成为移动的新问题。以上操作的实质是把移动n个盘子的问题转化为移动n-1个盘,那一、三步如何解决?事实上,上述方法设盘子数为n, n可为任意数,该法同样适用于移动n-1个盘。因此,依据上法,可解决n -1个盘子从A杆移到B杆(第一步)或从B杆移到C杆(第三步)问题。现在,问题由移动n个盘子的操作转化为移动n-2个盘子的操作。依据该原理,层层递推,即可将原问题转化为解决移动n -2、n -3… … 3、2,直到移动1个盘的操作,而移动一个盘的操作是可以直接完成的。至此,我们的任务算作是真正完成了。而这种由繁化简,用简单的问题和已知的操作运算来解决复杂问题的方法,就是递归法。在计算机设计语言中,用递归法编写的程序就是递归程序。
为了方便分析,下面以3个盘子为例子(这里是将左边柱子的碟子移到中间柱子),移动过程动态展示如下:
3.代码实现:
递归实现:
#a:第一个柱子
#b:第二个柱子
#c:第三个柱子
def Hanoi(n, a,b,c):
if (n == 1):
print(a, "->", c)
else:
Hanoi(n-1,a,c,b)#将a柱子上的n-1个盘子移动到b柱子上
Hanoi(1, a,b,c)#将a柱子上最后一个盘子移动到c柱子上
Hanoi(n-1,b,a,c)#将b柱子上的n-1个盘子移动到c柱子上
Hanoi(3,"a","b","c")
补充:注意主函数的参数含义·(碟子数,起始柱,中间柱,目标柱),同时值得注意的是主函数参数传导,按照位置一一对应传导,正因如此,移动a,b,c,就可以实现柱子之间的交换。
非递归实现(利用堆栈):
1.定义栈类:
class SqStack:#定义栈类
def __init__(self):#用数组替代栈
self.data=[]
def empty(self):#判空方法
if len(self.data)==0:
return True
return False
def push(self,e):#压栈方法,一个元素右压栈
self.data.append(e)
def pop(self):#出栈方法,判空后一个元素右出栈
assert not self.empty()
return self.data.pop()
def gettop(self):#判空后获取栈顶元素
assert not self.empty()
return self.data[len(self.data)-1]
if __name__=='__main__':#主函数验证栈类
st=SqStack()
st.push(1)
st.push(2)
st.push(3)
st.push(4)
print("出栈顺序:",end=' ')
while not st.empty():
print(st.pop(),end=' ')
print()
2.定义问题类:
class Question:#定义问题类
def __init__(self,m,a,b,c,N):
self.m=m
self.a=a#开始
self.b=b#借助
self.c=c#目标
self.N=N#递归树层数3.主函数:
方式1:利用数组充当堆栈
#用堆栈(先进后出)
from SqStack import SqStack#导入自定义栈模块(注意得在同一包下才可以导入)
from Question import Question#导入自定义问题模块
def Hanoi(n):
st=SqStack()#实例化栈
p=Question(n,'a','b','c')
st.push(p)#原始问题压栈
while not st.empty():
p=st.pop()#默认弹出栈顶元素
if p.m==1:
print("{}->{}".format(p.a,p.c))
else:
# 子问题压栈,由于先进后出,所以子问题应当以相反的顺序进栈
b=Question(p.m-1,p.b,p.a,p.c)##将b柱子上的n-1个盘子移动到c柱子上
st.push(b)
b=Question(1,p.a,p.b,p.c)#将a柱子上最后一个盘子移动到c柱子上
st.push(b)
b=Question(p.m-1,p.a,p.c,p.b)#将a柱子上的n-1个盘子移动到b柱子上
st.push(b)
n=eval(input("请输入汉诺塔的层数:"))
Hanoi(n)方式2:利用单向队列充当堆栈:
from collections import deque#python内置库
from Question import Question#导入自定义问题模块
def Hanoi(n):
st=deque()#队列实例化
p=Question(n,'a','b','c')
st.append(p)#初始问题进队(默认都是右进队)
while len(st) != 0:
p=st.pop()#队头元素出队(默认都是右出队)想知道pop()函数用法可以ctrl+b查看源码
if p.m==1:
print("{}->{}".format(p.a,p.c))
else:
b=Question(p.m-1,p.b,p.a,p.c)##将b柱子上的n-1个盘子移动到c柱子上
st.append(b)
b=Question(1,p.a,p.b,p.c)##将a柱子上最后一个盘子移动到c柱子上
st.append(b)
b=Question(p.m-1,p.a,p.c,p.b)##将a柱子上的n-1个盘子移动到b柱子上
st.append(b)
n=eval(input("请输入汉诺塔的层数:"))
Hanoi(n)补充:队列的特点就是先进先出,当然这个是对于双端队列来说的。
单端队列其实就相当于堆栈。
数组和序列可以替代堆栈和队列。
非递归代码思路讲解:
不用递归用循环,就需要用到堆栈先进后出的特性来模拟递归,将问题放入堆栈,然后不断将栈顶问题分解,将分解的n-1个问题放入堆栈,这样循环直到堆栈为空。于是我们需要自定义一个问题类,如果采用方式1,那么就需要自定义一个栈类,如果采用方式2,直接导入python的deque内置模块。下面还是以3个盘子为例子:
为了直观点,我手绘了几张图片解析,虽然画得不咋地,希望不会影响到大家的观感,哈哈哈!
利用递归树深层理解递归:
深度优先遍历(DFS):顾名思义,深度优先遍历就是找准一条路不停深入的搜索方法,当发现这条路走不通的时候就会回退到上一个探索的节点,如果上一个节点存在没有探索的分支,便继续探索若没有则继续回退。深度优先遍历就有点像二叉树中的前序、中序和后序遍历。
深度优先遍历的关键就在于如何找到已经探索过节点的上一个节点,也就是如何回溯。
通俗理解:一条路走到底,直到无路可走,才浪子回头。
所以根据中序遍历,先从解决完左子树(n-1,a,c,b)的子问题,再打印子问题(1,a,b,c),最后解决右子树(n-1,b,a,c)的子问题。下面还是本人的“精致”绘图帮助大家理解:
图表内容说明:
原始:表示原始问题,以原始问题作为跟结点
始:表示子问题——以C盘为中介,从A杆将1至n-1号盘移至B杆;
中:表示子问题——将A杆中剩下的第n号盘移至C杆;
末:表示子问题——以A杆为中介;从B杆将1至n-1号盘移至C杆
本人的理解是:
递归相当于深度优先遍历,深度优先遍历在遍历树时相当于中序遍历。