PyTorch深度学习实践概论笔记8练习-kaggle的Titanic数据集预测(一)数据分析
刘老师在第8讲PyTorch深度学习实践概论笔记8-加载数据集中留下一个练习:对kaggle上的Titanic数据集,使用DataLoader类进行分类,训练目标是预测某位乘客是否活下来(Survived)。本篇文章先读取数据和做一些简单的数据分析,熟悉一下数据集。
数据特征包含下面这些:
![]()
官网给的数据解释如下。
0 Overview
数据集被划分为训练集和测试集:
- training set (train.csv)
- test set (test.csv)
训练集应该被用来建立你的机器学习模型。对于训练集,我们为每个乘客提供结果(也称为“ground truth”)。你的模型将基于乘客的性别和阶级等“特征”。您还可以使用特征工程来创建新的特征。
测试集应该用来查看您的模型在不可见数据上的性能。对于测试集,我们不为每个乘客提供基本真相。你的工作就是预测这些结果。对于测试中的每一位乘客,使用你训练的模型来预测他们是否在泰坦尼克号沉没时幸存下来。
还包括gender_submit .csv,这是一组假设所有且只有女性乘客能够存活的预测,作为提交文件的示例。
Data Dictionary-数据词典
| Variable(变量名) | Definition(定义) | Key(取值) |
|---|---|---|
| PassengerId | 乘客编号 | 1-891 |
| Survived | Survival(是否生存) | 0和1。0 = 死亡, 1 = 存活 |
| Pclass | Ticket class(票的等级,社会经济地位(SES)的代表。) | 1 = 1st, 2 = 2nd, 3 = 3rd 1 =上;2 =中间;3 =低 |
| Name | 乘客姓名 | 例如Braund,Mr. Owen Harris |
| Sex | Sex(性别) | male,female |
| Age | Age in years(年龄) | 数字(float64)。如果年龄小于1,则为小数;如果估计年龄,是xx.5,有缺失 |
| SibSp | # of siblings / spouses aboard the Titanic (泰坦尼克号上的兄弟姐妹/配偶) Sibling=兄弟,姐妹,继兄弟,继姐妹 pouse=丈夫,妻子(情妇和未婚夫被忽略) |
0-8 |
| Parch | # of parents / children aboard the Titanic (泰坦尼克号上的父母/孩子) Parent =母亲,父亲 Child=女儿、儿子、继女、继子 有些孩子外出旅行只带了一个保姆,因此对他们来说parch=0 |
0-6 |
| Ticket | Ticket number(票号) | 例如A/5 21171、PC 17599 |
| Fare | Passenger fare(乘客票价) | 数字(float64),有缺失 |
| Cabin | Cabin number(船舱号码) | 例如C85,提取A/B/C/D等,有缺失 |
| Embark | Port of Embarkation(登船港口) | C = Cherbourg, Q = Queenstown, S = Southampton,有缺失 |
整个数据量不大,训练集和测试集加起来总共891+418=1309个。
1 前期数据分析
拿到这笔数据,我们先大概分析一下数据,目的是初步了解数据之间的相关性,为之后的特征选择和建模预测做准备。参考知乎的一篇文章:pytorch练习:泰坦尼克号生存预测 - 知乎
1.1 读取数据
读取数据的代码如下:
#导入需要的库
import re
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 读取数据的地址修改成自己的地址
train = pd.read_csv("./titanic/train.csv")
test = pd.read_csv("./titanic/test.csv")
print("train.shape:",train.shape,"test.shape:",test.shape)#输出训练集和测试集大小
total_data = train.append(test,sort=False,ignore_index=True)#合并训练集和测试集
print("total_data.shape",total_data.shape)
total_data.head() #查看前5行数据输出训练集train.shape为(891, 12),测试集test.shape为(418, 11),合并之后的数据total_data.shape为(1309, 12)。前5行数据如下:
查看train和test数据集的基本信息:
train.info()
print("*"*50)
test.info()输出如下:
可以看到训练集的Age、Cabin、Embarked存在丢失数据;测试集的Age、Fare、Cabin存在丢失数据(这些变量之后都需要做缺失值处理)。
1.2 特征分析
接下来我们进行数据分析,由于该练习是预测乘客的存活情况,因此主要分析特征Survived和其他特征的关系。
1.2.1 总体生存率情况(Survived)
total_data['Survived'].value_counts().plot.pie(autopct="%1.2f%%")整个数据集(训练集)中存活342人,死亡549人,存活率38.38%,死亡率61.62%。
1.2.2 不同性别的人员存活率分析(Sex、Survived)
print(total_data.groupby(['Sex'])['Survived'].agg(['count','mean']))
plt.figure(figsize=(10,5))
sns.countplot(x='Sex',hue='Survived',data=total_data)
plt.title('Sex vs Survived')| count | mean | |
| female | 314 | 0.742038 |
| male | 577 | 0.188908 |
图像如下:
整个数据集中男性人数577,女性314人,男性占比64.75%,但女性的存活率74.2%远高于男性存活率18.8%,这让我想到电影《泰坦尼克号》中让妇女和儿童先上救生艇,是否有关联?(存活率与性别有关)。
1.2.3 不同登船港的人员存活率分析(Embarked、Survived)
首先,查看Embarked的分布。
total_data.Embarked.value_counts()输出:
由于该特征存在缺失,下面做缺失值处理,用众数填充。
total_data['Embarked'].fillna(total_data.Embarked.mode().values[0],inplace=True)缺失值处理之后输出:
查看不同登船港人员的存活率。
print(total_data.groupby(['Embarked'])['Survived'].agg(['count','mean']))
plt.figure(figsize=(10,5))
sns.countplot(x='Embarked',hue='Survived',data=total_data)
plt.title('Embarked vs Survived')可以看到,C地登船的存活率最高、其次为Q地登船、S地登船人数最多但存活率仅有1/3(存活率与登船港有关)。
1.2.4 不同船舱号的人员存活率分析(Cabin、Survived)
由于Cabin缺失比较严重,用Unknown替代缺失值。先做缺失值处理。
total_data['Cabin'].fillna('U',inplace=True)查看不同船舱号人员的存活率,代码如下:
total_data['Cabin'] = total_data['Cabin'].map(
lambda x:re.compile('([a-zA-Z]+)').search(x).group())
print(total_data.groupby(['Cabin'])['Survived'].agg(['count','mean']))
plt.figure(figsize=(10,5))
sns.countplot(x='Cabin',hue='Survived',data=total_data)
plt.title('Cabin vs Survived')不同船舱号人员的存活情况图像如下:
结合之前的分析,有船舱号信息的人员占(204+91)/1309=22.54%,缺失船舱号的群体占比77.5%,但是存活率仅仅29.99%。 船舱号B/D/E存活率较高,均超过70%(存活率与船舱号有关)。
1.2.5 不同票等级的人员存活率分析(Pclass、Survived)
查看不同票等级人员的存活率情况。
print(total_data.groupby(['Pclass'])['Survived'].agg(['count','mean']))
plt.figure(figsize=(10,5))
sns.countplot(x='Pclass',hue='Survived',data=total_data)
plt.title('Pclass vs Survived')数据表明,票等级越高存活率就越高;等级1的人存活率62.96%;等级3的人数占比超50%,但存活率不到1/3(0.242363)(存活率与票等级有关)。
1.2.6 不同票等级的男女存活率分析(Pclass、Sex、Survived)
考虑不同票等级中男女生存的几率。
print(total_data[['Sex','Pclass','Survived']].groupby(
['Pclass','Sex']).agg(['count','mean']))
total_data[['Sex','Pclass','Survived']].groupby(
['Pclass','Sex']).mean().plot.bar(figsize=(10,5))
plt.xticks(rotation=0)
plt.title('Sex,Pclass vs Survived')结果表明,不同票等级下女性的存活率均高于男性,在票等级1和2中女性存活率均超过90%。
1.2.7 不同票价的人员存活率分析(Fare、Survived)
由于票价有缺失,首先结合Pclass的平均票价,对Fare进行缺失值处理。首先看一下不同票等级的票价,代码如下:
total_data[['Pclass','Fare']].groupby(['Pclass'], as_index=False).mean()
#total_data['Fare'].groupby(by=total_data['Pclass']).mean()缺失值处理:
total_data['Fare'] = total_data[['Fare']].fillna(
total_data.groupby('Pclass').transform(np.mean))
total_data['Fare'].describe()处理之后的输出结果:
查看票价分布情况,画直方图。
plt.figure(figsize=(10,5))
total_data['Fare'].hist(bins=70)
plt.title('Fare Distribution')直方图说明数据集的票价集中在低价区。进一步分析票价和存活率的关系:
total_data.boxplot(column='Fare',by='Survived',showfliers=False,figsize=(10,5))上述箱线图表明,存活群体的票价均值要高于死亡群体,而且存活的群体中票价分布差异更大。
更进一步分析,我们划分票价区间,查看票价区间的存活率情况。
1.2.8 不同票价区间的人员存活率分析(Fare_bin、Survived)
将票价划分为四个区间。
bins_fare = [0,8,14,31,515]
total_data['Fare_bin'] = pd.cut(total_data['Fare'], bins_fare, right=False)
#画图
print(total_data[['Fare_bin', 'Survived']].groupby(
'Fare_bin')['Survived'].agg(['count', 'mean']))
plt.figure(figsize=(10, 5))
sns.countplot(x='Fare_bin', hue='Survived', data=total_data)
plt.title('Fare and Survived')随着票价的升高,票价区间的存活率越来越高,[31,515)的存活率为58.2%(存活率与票价有关)。
1.2.9 不同票等级[细分]的人员存活率分析(Pclass_Fare_Category、Survived)
对票等级按不同价格细分:
total_data.boxplot(column='Fare', by='Pclass',showfliers=False, figsize=(10, 5))上图说明票等级越高,票价相对更贵,但是同一个票等级的票价差异较大,进一步对同一票价等级按照价格进行细分。
def pclass_fare_category(df, pclass1_mean_fare, pclass2_mean_fare, pclass3_mean_fare):
if df['Pclass'] == 1:
if df['Fare'] <= pclass1_mean_fare:
return 'Pclass1_Low'
else:
return 'Pclass1_High'
elif df['Pclass'] == 2:
if df['Fare'] <= pclass2_mean_fare:
return 'Pclass2_Low'
else:
return 'Pclass2_High'
elif df['Pclass'] == 3:
if df['Fare'] <= pclass3_mean_fare:
return 'Pclass3_Low'
else:
return 'Pclass3_High'
Pclass_mean = total_data['Fare'].groupby(by=total_data['Pclass']).mean()
Pclass1_mean_fare = Pclass_mean[1]
Pclass2_mean_fare = Pclass_mean[2]
Pclass3_mean_fare = Pclass_mean[3]
total_data['Pclass_Fare_Category'] = total_data.apply(pclass_fare_category, args=(
Pclass1_mean_fare, Pclass2_mean_fare, Pclass3_mean_fare), axis=1)
print(total_data[['Pclass_Fare_Category', 'Survived']].groupby(
'Pclass_Fare_Category')['Survived'].agg(['count', 'mean']))
plt.figure(figsize=(10, 5))
sns.countplot(x='Pclass_Fare_Category', hue='Survived', data=total_data)
plt.title('Pclass_Fare_Category and Survived')根据同一票等级的均值划分,最终得到6个票等级,Pclass_Fare_Category的生存率结果如下:
数据说明,同一票等级的高价格区间的存活率高于低价格区间。
1.2.10 不同title[name中提取]的人员存活率分析(Title、Survived)
名字中出现了一些Dr、Officer、Lady等一些title,我们提取name中的title,对title进行归类,主要有这六类:
代码如下:
def sub_title(x):
return re.search('([A-Za-z]+)\.', x).group()[:-1]
total_data['Title'] = total_data['Name'].apply(lambda x: sub_title(x))
# 对title进行归类
title_Dict = {}
title_Dict.update(dict.fromkeys(
['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer'))
title_Dict.update(dict.fromkeys(
['Don', 'Sir', 'Countess', 'Dona', 'Lady'], 'Royalty'))
title_Dict.update(dict.fromkeys(['Mme', 'Ms', 'Mrs'], 'Mrs'))
title_Dict.update(dict.fromkeys(['Mlle', 'Miss'], 'Miss'))
title_Dict.update(dict.fromkeys(['Mr'], 'Mr'))
title_Dict.update(dict.fromkeys(['Master', 'Jonkheer'], 'Master'))
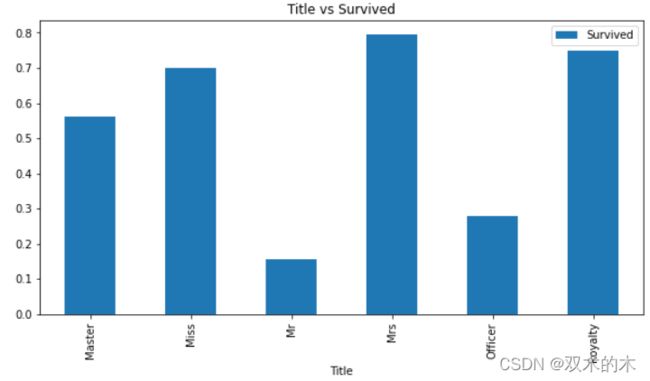
total_data['Title'] = total_data['Title'].map(title_Dict)不同title的存活率情况:
total_data[['Title', 'Survived']].groupby(
['Title']).mean().plot.bar(figsize=(10, 5))
plt.title('Title vs Survived')Mr和Officer的人员存活率明显更低,Mrs title的群体存活率最高(存活率与title有关)。
1.2.11 不同name长度的人员存活率分析(Name_length、Survived)
提取name的长度信息。
plt.figure(figsize=(18, 5))
total_data['Name_length'] = total_data['Name'].apply(len)
name_length = total_data[['Name_length', 'Survived']].groupby(
['Name_length'], as_index=False).mean()
sns.barplot(x='Name_length', y='Survived', data=name_length)
plt.title('Name length vs Survived')名字长度小于35的群体的存活率相对较低,名字长度越长,存活率整体越高。但是看了一下,后面名字长度长的人数基本是个位数的(存活率与名字长度有关)。
1.2.12 区分有无兄弟姐妹/配偶在船上的人员存活率分析(SibSp、Survived)
区分有无兄弟姐妹/配偶在船上的两个群体进行数据对比。
sibsp_df = total_data[total_data['SibSp'] != 0] #有兄弟姐妹/配偶
no_sibsp_df = total_data[total_data['SibSp'] == 0] #无
plt.figure(figsize=(10, 5))
plt.subplot(121)
sibsp_df['Survived'].value_counts().plot.pie(
labels=['No Survived', 'Survived'], autopct='%1.1f%%')
plt.xlabel('sibsp')
plt.subplot(122)
no_sibsp_df['Survived'].value_counts().plot.pie(
labels=['No Survived', 'Survived'], autopct='%1.1f%%')
plt.xlabel('no_sibsp')饼图如下:
明显看出,(左侧)有兄弟姐妹/配偶在船上的存活率更高,为46.6%(存活率与SibSp有关)。
1.2.13 区分有无父母/子女在船上的人员存活率分析(Parch、Survived)
区分有无父母/子女在船上在船上的两个群体进行数据对比。
parch_df = total_data[total_data['Parch'] != 0] #有父母/子女
no_parch_df = total_data[total_data['Parch'] == 0] #无
plt.figure(figsize=(10, 5))
plt.subplot(121)
parch_df['Survived'].value_counts().plot.pie(
labels=['No Survived', 'Survived'], autopct='%1.1f%%')
plt.xlabel('Parch')
plt.subplot(122)
no_parch_df['Survived'].value_counts().plot.pie(
labels=['No Survived', 'Survived'], autopct='%1.1f%%')
plt.xlabel('no_Parch')明显看出,(左侧)有父母/子女在船上的成活率更高,为48.8%(存活率与Parch有关)。
1.2.14 不同家庭人数[合并]的人员存活率分析(Family_Size、Survived)
查看不同家庭人数的存活率,首先Parch和SibSp分开查看。
fig, ax = plt.subplots(1, 2, figsize=(18, 8))
total_data[['Parch', 'Survived']].groupby(['Parch']).mean().plot.bar(ax=ax[0])
ax[0].set_title('Parch vs Survived')
total_data[['SibSp', 'Survived']].groupby(['SibSp']).mean().plot.bar(ax=ax[1])
ax[1].set_title('SibSp vs Survived')然后,合并家庭人数。
total_data['Family_Size'] = total_data['Parch'] + total_data['SibSp'] + 1
total_data[['Family_Size', 'Survived']].groupby(
['Family_Size']).mean().plot.bar(figsize=(10, 5))
plt.title('Family size vs Survived')上图说明有家庭成员的存活率大概率比无家庭成员的存活率高,家庭人员=4时存活率最高,但随着人数越高存活率降低。
根据上述结果重新划分家庭大小,家庭人员以4为界。
def family_size_category(family_size):
if family_size <= 1:
return 'Single'
elif family_size <= 4:
return 'Small_Family'
else:
return 'Large_Family'
total_data['Family_Size_Category'] = total_data['Family_Size'].map(
family_size_category)
total_data[['Family_Size_Category','Survived']].groupby(['Family_Size_Category']).mean().plot.bar(figsize=(10,5))上述直方图说明,家庭总人数大于4的家庭存活率最低,总人数等于1的高一些,总人数小于4的家庭存活率最高,57.9%。
1.2.15 不同年龄的人员存活率分析(Age、Survived)
Age(年龄)也有缺失值,这里我们使用随机森林预测缺失的年龄。首先,将将分类变量转化为数值,使用pd.factorize()函数。
#pd.factorize()做的是“因式分解”,把常见的字符型变量分解为数字
total_data['Embarked'], uniques_embarked = pd.factorize(total_data['Embarked'])
total_data['Sex'], uniques_sex = pd.factorize(total_data['Sex'])
total_data['Cabin'], uniques_cabin = pd.factorize(total_data['Cabin'])
total_data['Fare_bin'], uniques_fare_bin = pd.factorize(total_data['Fare_bin'])
total_data['Pclass_Fare_Category'], uniques_pclass_fare_category = pd.factorize(
total_data['Pclass_Fare_Category'])
total_data['Title'], uniques_title = pd.factorize(total_data['Title'])
total_data['Family_Size_Category'], uniques_family_size_category = pd.factorize(
total_data['Family_Size_Category'])接着,训练随机森林模型进行年龄预测,代码如下:
import sklearn
from sklearn.ensemble import RandomForestRegressor
ageDf = total_data[['Age', 'Pclass', 'Title', 'Name_length',
'Sex', 'Family_Size', 'Fare', 'Cabin', 'Embarked']]
ageDf_notnull = ageDf.loc[ageDf['Age'].notnull()]
ageDf_isnull = ageDf.loc[ageDf['Age'].isnull()]
X = ageDf_notnull.values[:, 1:]
y = ageDf_notnull.values[:, 0]
RFR = RandomForestRegressor(n_estimators=1000, n_jobs=-1)
# 训练
RFR.fit(X, y)
predictAges = RFR.predict(ageDf_isnull.values[:, 1:])
total_data.loc[total_data['Age'].isnull(), 'Age'] = predictAges然后,查看填充后的年龄数据:
total_data['Age'].describe()最后,分析是否存活群体的年龄差异:
# 查看年龄分布
plt.figure(figsize=(18, 5))
plt.subplot(131)
total_data['Age'].hist(bins=70)
plt.xlabel('Age')
plt.ylabel('Num')
plt.subplot(132)
total_data.boxplot(column='Age', showfliers=False)
# 查看是否存活群体的年龄差异
plt.subplot(133)
sns.boxplot(x='Survived', y='Age', data=total_data)箱形图显示是否存活群体的年龄差异并不大,最大值、最小值和平均值大小都差不多,而且都存在异常值(定义为小于Q1-1.5IQR或大于Q3+1.5IQR的值)。
进一步分析票等级和性别不同年龄的存活分布:
fig, ax = plt.subplots(1, 2, figsize=((18, 8)))
# 查看不同票等级不同年龄的存活分布
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0, 110, 10))
sns.violinplot(x='Pclass', y='Age', hue='Survived',
data=total_data, split=False, linewidth=2, ax=ax[0])
# 查看不同性别不同年龄的存活分布
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0, 110, 10))
sns.violinplot(x="Sex", y="Age", hue="Survived",
data=total_data, split=False, linewidth=2, ax=ax[1])图像如下:
小提琴图 (Violin Plot)是用来显示多组数据的分布状态以及概率密度,它结合了箱形图和密度图的特征,主要用来显示数据的分布形状,在数据量很大的时候小提琴图特别适用。通过上面分组小提琴图,我们发现在不同票等级中存活下来的人员年龄相对更小(左),不同性别人员的存活与否年龄差异并不大(右)。
1.2.16 不同年龄分层的人员存活率分析(Age_group、Survived)
查看不同年龄的存活分布:
facet = sns.FacetGrid(total_data, hue='Survived', aspect=4)
facet.map(sns.kdeplot, 'Age', shade=True)
facet.set(xlim=(0, total_data['Age'].max()))
facet.add_legend()进一步,对年龄分层处理:
bins = [0, 12, 18, 65, 100]
total_data['Age_group'] = pd.cut(total_data['Age'], bins)
print(total_data.groupby('Age_group')['Survived'].agg(['count', 'mean']))
plt.figure(figsize=(10, 5))
sns.countplot(x='Age_group', hue='Survived', data=total_data)
plt.title('Age group vs Survived')可以看到年幼群体的群体的存活率最高,超过一半,为56.4%。
1.3 相关性分析
接下来,整体看一下数据的相关性。
total_data['Age_group'], uniques_age_group = pd.factorize(total_data['Age_group'])
Correlation = pd.DataFrame(total_data[[
'Survived', 'Embarked', 'Sex', 'Title', 'Name_length', 'Family_Size', 'Family_Size_Category',
'Fare', 'Fare_bin', 'Pclass', 'Pclass_Fare_Category', 'Age', 'Age_group', 'Cabin'
]])
# 查看数据相关性
colormap = plt.cm.viridis
plt.figure(figsize=(14, 12))
plt.title('Pearson Correlation of Features', y=1.05, size=15)
sns.heatmap(
Correlation.astype(float).corr(method='kendall'),
linewidths=0.1,
vmax=1.0,
square=True,
cmap=colormap,
linecolor='white',
annot=True)特征的皮尔逊相关系数图如下:
变量关系组图的代码如下:
g = sns.pairplot(
total_data[[
'Survived', 'Pclass', 'Sex', 'Age', 'Fare', 'Embarked', 'Family_Size',
'Title', 'Cabin'
]],
hue='Survived',
palette='seismic',
height=1.2,
diag_kind='kde',
diag_kws=dict(shade=True),
plot_kws=dict(s=10))
g.set(xticklabels=[])图像如下:
1.4 数据预处理
为了之后的预测能更好地构建模型,将变量进行one-hot编码处理和数据标准化处理。
1.4.1 one-hot编码处理
# 对分类变量进行独热编码
pclass_dummies = pd.get_dummies(total_data['Pclass'], prefix='Pclass')
total_data = total_data.join(pclass_dummies)
title_dummies = pd.get_dummies(total_data['Title'], prefix='Title')
total_data = total_data.join(title_dummies)
sex_dummies = pd.get_dummies(total_data['Sex'], prefix='Sex')
total_data = total_data.join(sex_dummies)
cabin_dummies = pd.get_dummies(total_data['Cabin'], prefix='Cabin')
total_data = total_data.join(cabin_dummies)
embark_dummies = pd.get_dummies(total_data['Embarked'], prefix='Embarked')
total_data = total_data.join(embark_dummies)
bin_dummies_df = pd.get_dummies(total_data['Fare_bin'], prefix='Fare_bin')
total_data = total_data.join(bin_dummies_df)
family_size_dummies = pd.get_dummies(
total_data['Family_Size_Category'], prefix='Family_Size_Category')
total_data = total_data.join(family_size_dummies)
pclass_fare_dummies = pd.get_dummies(
total_data['Pclass_Fare_Category'], prefix='Pclass_Fare_Category')
total_data = total_data.join(pclass_fare_dummies)
age_dummies = pd.get_dummies(total_data['Age_group'], prefix='Age_group')
total_data = total_data.join(age_dummies)1.4.2 标准化处理
from sklearn.preprocessing import StandardScaler
scale_age_fare = StandardScaler().fit(
total_data[['Age', 'Fare', 'Name_length']])
total_data[['Age', 'Fare', 'Name_length']] = scale_age_fare.transform(
total_data[['Age', 'Fare', 'Name_length']])
total_data_backup = total_data.drop(['PassengerId', 'Pclass', 'Name', 'Sex', 'SibSp', 'Parch',
'Ticket', 'Fare', 'Cabin', 'Embarked', 'Fare_bin', 'Pclass_Fare_Category', 'Title',
'Family_Size', 'Family_Size_Category', 'Age_int', 'Age_group'
], axis=1, errors='ignore')
total_data_backup.columns输出如下:
Index(['Survived', 'Age', 'Name_length', 'Pclass_1', 'Pclass_2', 'Pclass_3',
'Title_0', 'Title_1', 'Title_2', 'Title_3', 'Title_4', 'Title_5',
'Sex_0', 'Sex_1', 'Cabin_0', 'Cabin_1', 'Cabin_2', 'Cabin_3', 'Cabin_4',
'Cabin_5', 'Cabin_6', 'Cabin_7', 'Cabin_8', 'Embarked_0', 'Embarked_1',
'Embarked_2', 'Fare_bin_0', 'Fare_bin_1', 'Fare_bin_2', 'Fare_bin_3',
'Family_Size_Category_0', 'Family_Size_Category_1',
'Family_Size_Category_2', 'Pclass_Fare_Category_0',
'Pclass_Fare_Category_1', 'Pclass_Fare_Category_2',
'Pclass_Fare_Category_3', 'Pclass_Fare_Category_4',
'Pclass_Fare_Category_5', 'Age_group_0', 'Age_group_1', 'Age_group_2',
'Age_group_3'],
dtype='object')1.4.3 保存处理好的数据文件
为了下次的建模,注意保存处理好的数据文件,分开保存train和test数据集的代码如下:
train_data = total_data_backup[:891]
train_data.to_csv("./titanic/titanic_train.csv")
test_data = total_data_backup[891:]
test_data.to_csv("./titanic/titanic_test.csv")由于篇幅有点长,建模预测部分放在另外一篇文章,链接请看评论区。
说明:记录学习笔记,如果错误欢迎指正!写文章不易,转载请联系我。