因子分析——matlab
目录
一、起源
二、基本思想
三、算法用途
四、实例详解
1.读取数据
2.数据标准化
3.两种不同的做法
3.1 不用函数
3.2 factoran()法
4.对因子得分进行排序
5.对因子得分进行画图
一、起源
因子分析的起源是这样的:1904年英国的一个心理学家发现学生的英语、法语和古典语成绩非常有相关性,他认为这三门课程背后有一个共同的因素驱动,最后将这个因素定义为“语言能力”。
基于这个想法,发现很多相关性很高的因素背后有共同的因子驱动,从而定义了因子分析,这便是因子分析的由来。
二、基本思想
我们再通过一个更加实际的例子来理解因子分析的基本思想:
现在假设一个同学的数学、物理、化学、生物都考了满分,那么我们可以认为这个学生的理性思维比较强,在这里理性思维就是我们所说的一个因子。在这个因子的作用下,偏理科的成绩才会那么高。
到底什么是因子分析?就是假设现有全部自变量x的出现是因为某个潜在变量的作用,这个潜在的变量就是我们说的因子。在这个因子的作用下,x能够被观察到。
因子分析就是将存在某些相关性的变量提炼为较少的几个因子,用这几个因子去表示原本的变量,也可以根据因子对变量进行分类。
因子分子本质上也是降维的过程,和主成分分析(PCA)算法比较类似。
三、算法用途
因子分析法和主成分分析法有很多类似之处。因子分析的主要目的是用来描述隐藏在一组测量到的变量中的一些更基本的,但又无法直接测量到的隐性变量。因子分析法也可以用来综合评价。
其主要思路是利用研究指标的之间存在一定的相关性,从而推想是否存在某些潜在的共性因子,而这些不同的潜在的共性因子不同程度地共同影响着研究指标。因子分析可以在许多变量中找出隐藏的具有代表性的因子,将共同本质的变量归入一个因子,可以减少变量的数目。
四、实例详解
![]()
数据来源于中国统计年鉴。
1.读取数据
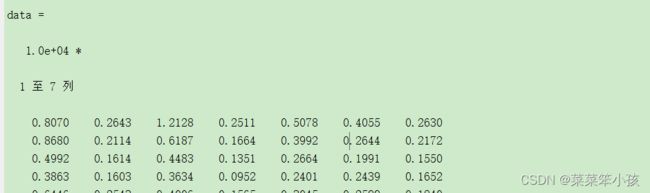
[data,textdata] = xlsread('D:\桌面\aa.xls')%读取数据
让我们来看一下,读取的 data 和 textdata
然后我们在读取一下变量名
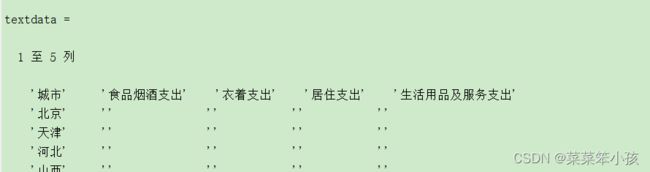
varname = textdata(1,2:end)%提取textdata的第1行,第2至最后一列,即变量名运行结果:
最后我们再看一下它的每行的首项,在这突然不知道叫啥了。。。。
obsname = textdata(2:end,1)%提取textdata的第1列,第2行至最后一行,即地区名运行结果为:
2.数据标准化
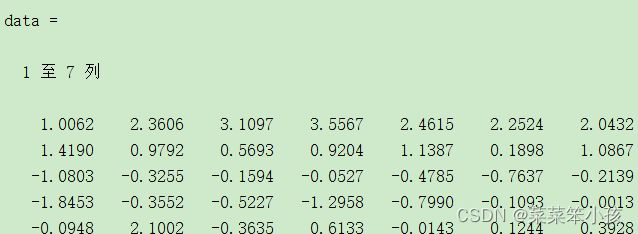
标准化的数据均值为0,标准差为1;就是原数据减去均值,再除以标准差(无偏估计)
![]()
data=zscore(data) %数据标准化运行结果:
3.两种不同的做法
3.1 不用函数
3.1.1 求相关系数矩阵
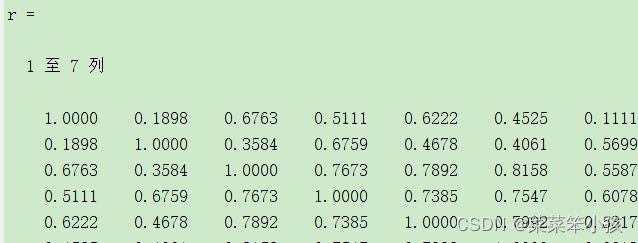
r=corrcoef(data) %相关系数矩阵运行结果:
3.1.2 带入主成分分析进行计算
%进行主成分分析的相关计算
%vec是r的特征向量,val为r的特征值,con为各个主成分的贡献率
[vec,val,con]=pcacov(r); %进行主成分分析的相关计算3.1.3 求载荷矩阵
f1=repmat(sign(sum(vec)),size(vec,1),1);
vec=vec.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec,1),1);
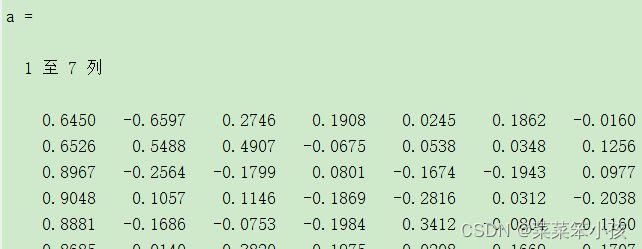
a=vec.*f2 %求初等载荷矩阵 运行结果:
3.1.4 因子旋转(最大方差法)
num=input('请选择主因子的个数:'); %选择主因子的个数
%其中b为旋转后的载荷矩阵,t为变换的正交矩阵
[b,t]=rotatefactors(a(:,1:num),'method', 'varimax'); %对载荷矩阵进行旋转
bz=[b,a(:,num+1:end)] %旋转后的载荷矩阵 选择两个因子并输出:
3.1.5 贡献率
gx=sum(bz.^2); %计算因子贡献
gxv=gx/sum(gx); %计算因子贡献率3.1.6 因子得分
dfxsh=inv(r)*b; %计算得分函数的系数
F=data*dfxsh ;%计算各个因子的得分3.2 factoran()法
这个函数具有一定的 bug 所以不太建议使用!!!
3.2.1因子旋转
%调用factoran函数根据原始观测数据作因子分析4
% 进行因子旋转(最大方差旋转法)
%在这里选择2个主因子进行输出
num=input('请选择主因子的个数:'); %选择主因子的个数
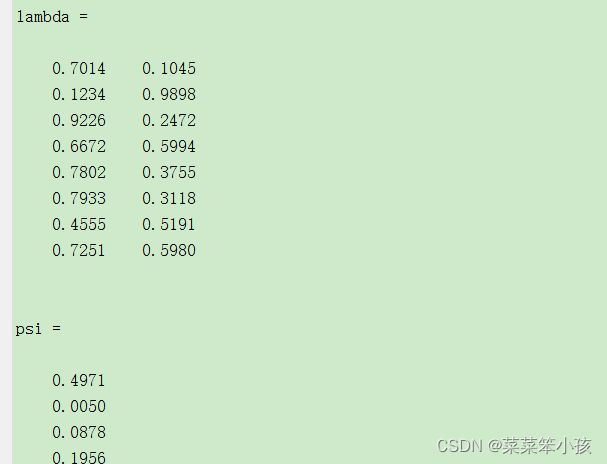
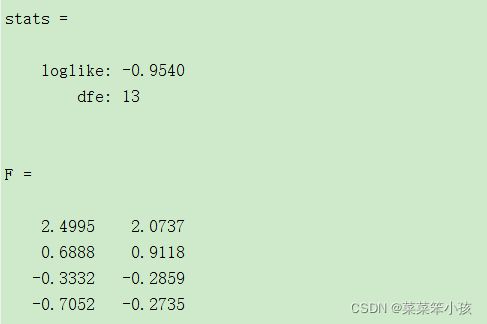
[lambda,psi,T,stats,F] = factoran(data,num)运行结果:
3.2.2 贡献率
%计算贡献率,因子载荷矩阵的列元素的平方和除以维数
gx = 100*sum(lambda.^2)/8
gxv = cumsum(Contribut) %计算累积贡献率3.2.3 因子得分
在上面 factoran() 函数的输出结果中就已经有了
4.对因子得分进行排序
%将因子得分F分别按因子得分1和因子得分2进行排序
obsF = [obsname, num2cell(F)] ;%将国家和地区名与因子得分刚在一个元胞数组中显示
F1 = sortrows(obsF, 2) ; % 按因子得分1排序
F2 = sortrows(obsF, 3); % 按因子得分2排序
head = {'地区','因子1','因子2'};
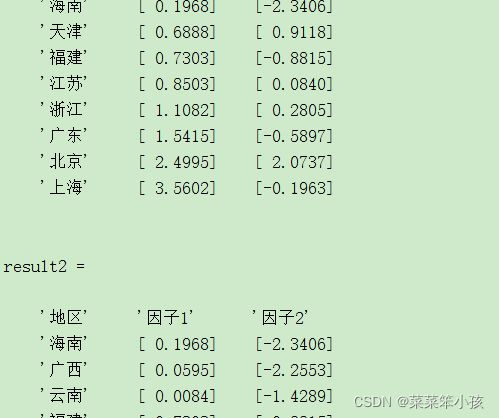
result1 = [head; F1]
result2 = [head; F2]输出:
5.对因子得分进行画图
在这里就表示一个的哦!!表示函数法那个吧,另一种自己试试吧,结果不太一样!!!
gname() 函数 ,你鼠标选中哪个点,进行击右键就会显示地区名
%绘制因子得分负值的散点图
plot(F(:,1),F(:,2),'k.');%作因子
xlabel('因子得分1');
ylabel('因子得分2');
gname(obsname);%交互式添加各散点的标注输出:
因子分析就到这里了,如果有不足之处,请大家及时指出,感谢!!