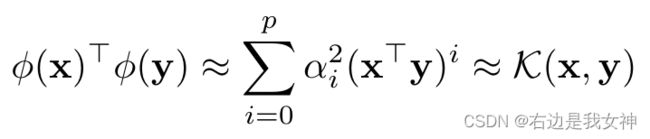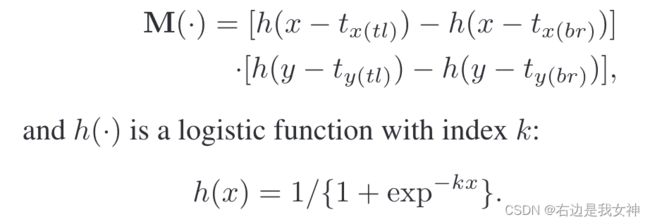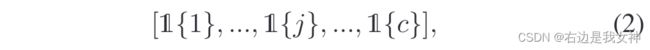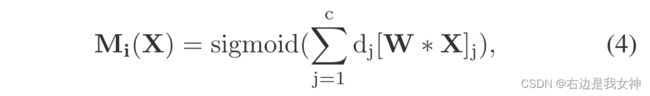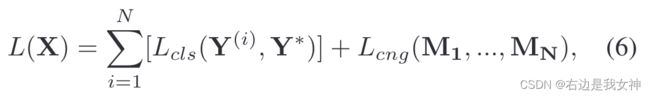细粒度图像分类论文研读-2017

Higher-order Integration of Hierarchical Convolutional Activations for Fine-grained Visual Categorization(by end-to-end feature encoding)

Abstract

细粒度视觉分类任务的成功依赖于各种语义部分的外观建模和相互联系。

这一特性使得FGVC任务非常具有挑战性，原因有三点：

1. 局部的注释和检测需要专家的指导；
2. 局部的大小不同；
3. 局部相互作用复杂且高阶。

为了解决上述问题，本文提出了一个基于分层卷积激活的高阶积分的端到端框架。

通过将卷积激活作为局部描述，分层卷积激活能够作为来自不同尺度的局部表示。（卷积激活是什么？为什么可以作为局部描述？）

本文提出了一个基于多项式核的预测器，目的是为了捕捉高阶统计量，用于建模零件之间的相互作用。为了模拟层间零件之间的相互作用，本文扩展了多项式预测器，通过核的融合来集成层次激活。

Introduction

全连接网络并不适合FGVC，而CNN中的局部的、有判别性的模式对于获得更有力量的表征是很关键的。

目前的方法一般都是先对局部进行定位，之后再对这些部位进行外观上的建模，以此在更深的层上面得到相应的局部特征。

全局的外观结构被包含进去来“pool these regional features”（大概的意思应该是对全局提特征之后把局部的特征抽取），这样的方法固然效果不错，但是存在以下几个问题：

1. 大量的基于局部的模型严重依赖细致的对局部的标注来训练准确的局部检测器，这样进一步限制了大规模数据集的可扩展性；此外，识别有区分度的局部对于特定的细粒度对象是很困难的，通常需要和人类或者专家之间的交互。
2. 有区分度的、有语义的部分通常以不同的尺度出现；每个空间单元都对应特定的感受野，因此用单一卷积层来描述不同的部件是有局限性的；
3. 开发单个对象部件的联合配置对于对象外观建模非常重要；一些工作提出了增加一些几何上的约束。现有方法只描述了极少数局部的一阶的存在性和关系，一旦这个局部变多了，那么这样一种描述的有效性就会被削弱。

综上所述，问题有三点：检测局部依赖人工、尺度问题、外观描述方式的欠缺。

因此，本文提出关注不同尺度下的高阶统计数据以提供一个更加灵活的方式来对全局的外观进行建模，此过程也不需要局部的注释。

关于核

最近的研究工作认为卷积滤波器可以看作弱的局部检测器，其激活的结果是看作检测的结果。

就是说，这个卷积直接就可以对局部有所反应，因此没必要特意把局部揪出来，直接对卷积的结果做文章即可。

本文提供了匹配核的视角来理解结合线性分类器的映射和池化结构。

线性映射和直接池化只能知道这个局部是否出现，为了获得局部之间的高阶关系，最好使用局部非线性匹配核来表征高阶局部的交互（co-occurrence）。难点在于如何在CNN结构中做到合理的插入。本文使用多项式核来建模更高级的局部交互。

关于多尺度

现有的研究以及广泛证实了融合神经网络中的分层特征是有益的，这主要是因为多个卷积层的不同辨别能力和由粗到细的描述。

然而，现有的方法简单地将多个激活进行级联或者相加来表示整体，或采用决策级融合来组合不同层的输出。这样的方法再利用层内或者层间卷积激活的内在高阶关系上受到限制。

Kernelized convolutional activations

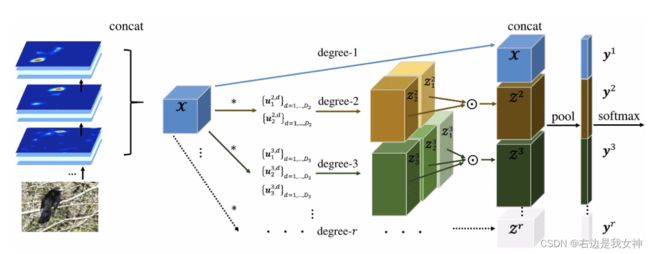
本文将卷积滤波器视为局部描述子，每个空间位置上的卷积激活视为部分描述。因此，本文引入多项式预测器来集成一系列局部匹配核，以建模高阶部件交互作用。

Matching kernel and polynomial predictor

后续的学习方式等内容不再赘述。

Hierarchical convolutional activations

Higher-order integration using kernel fusion

本部分主要探讨尺度的解决方案。

上图中的尖括号表示内积，其中的函数表示向量。

简而言之就是对不同输出层的结果进行层内的融合和层间的融合，公式应该表示的是element-wise的。

个人总结

本文的贡献有两个：

1. 混合多项式核的引入；
2. 尺度融合策略。
   

Kernel Pooling for Convolutional Neural Networks(by end-to-end feature encoding)

Abstract

具有双线性池化的卷积神经网络最初是完整的形式，之后才采用紧凑的表示形式。

这一模型成功的关键在于成对（二阶）特征交互的空间不变性建模。

在本文中提出了一个通用的池化框架。以核的形式捕捉特征的高阶交互。

本文演示了如何使用无参数的紧凑显式特征映射将诸如高斯RBF之类的核近似到给定的顺序。

Introduction

特征之间的交互的概念被广泛用作学习任务中的高阶表示。

背后的动机是是后续的线性分类器在更高维度的特征图上运行，使其具有更高阶的交互作用。通常有两种方法可以创建更高阶的交互。

最常见的是通过核技巧。

但缺点也存在两方面：

1. 所需的存储和评估时间都与训练数据的数量成正比，使得在大型数据集上效率低下；
2. 核的构造使得很难使用复杂的学习方法，包括SGD。

另一种方法是使用特征的乘积将特征向量显式映射到高维空间。

该方法的缺点比较明显：在d维度特征向量上进行p阶交互，那么这个特征映射将会达到$O(d^p)$。这在现实世界中是不切实际的。

前者是直接用低维数据得到高维信息，后者是计算得到高维数据。

本文提出了一种生成显式特征图的紧凑且可微的方法。在实际应用中，人们经常通过快速傅里叶变换和快速傅里叶逆变换在频域中进行循环卷积。一篇论文在理论和实践上都证明：该方法能够简洁地逼近多项式核。

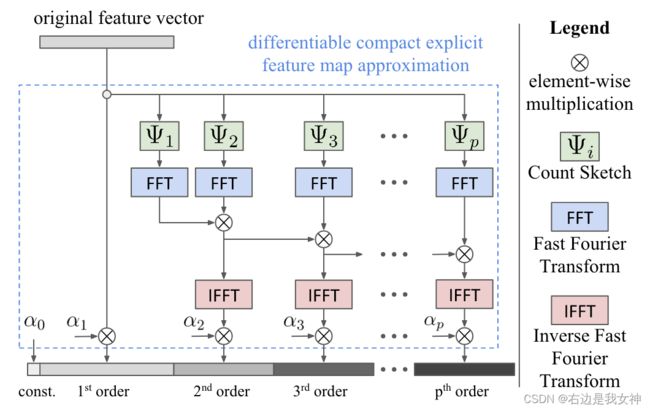
上图是本文提出的kernel pooling的具体实现，对于feature map中的每一个位置，使用Count Sketch来生成一个紧凑的特征映射。

在应用kernel pooling之后，两个特征之间的内积可以捕获高阶特征交互。这相当于下图的公式。

这使得后续的线性分类器具有高度的鉴别性。

最终的特征向量是全局平均池化的结果。

本文的工作有两个贡献：

1. 提出一种通过紧凑显式特征映射的通用内核池化方法；
2. 提出的内核池化方法是可区分的，并且可以和CNN结合进行联合优化。

Kernel Pooling

本文将池化的概念定义为编码并聚合feature map到一个全局特征向量的过程。

AlexNet/VGG 采用了全连接层+ReLU的策略，计算量大且参数多；

Inception/Residual Learning 采用了全局平均池化，计算量可观但没有捕捉高阶特征交互；

双线性模型，直接为二阶多项式核生成$c^2$维特征，之后使用Tensor Sketch进行逼近。

本文提出的模型超越双线性模型并捕捉高阶特征交互。首先定义了泰勒级数核，并证明了其显式特征映射可以被紧凑逼近。然后，我们演示了如何使用泰勒级数核的紧凑特征投影来逼近常用的核，如高斯径向基函数。

Explicit feature projection via Tensor product

因为显式表示的维度比较高，所以需要一种压缩近似的方法。

Compact approximate

Taylor series kernel

我们定义x的Count Sketch为：

可以看到C(x)是一个d维的向量，通过两个哈希函数计算得到。他们的输出分别为h:{1,2,…,d},s:{+1,-1}。

p阶x可以近似为：

其中，小圆圈表示element-wise的乘积。

于是，随着阶数的提升，总的特征维度呈现线性的增长。

Gaussian RBF kernel

这一节主要讲了泰勒核函数可以近似于高斯核函数。此处不再赘述。

总结

15年的B-CNN中介绍了特征交互的应用（先前也有文章），这是一种核技巧的显式应用（多项式核），本文进一步扩展为泰勒核。

因此，本文在本质上是介绍一种新的核技巧在特征交互中的应用效果。

Look Closer to See Better ：Recurrent Attention Convolutional Neural Network for Fine-grained Image Recognition(by localization-classification subnetwork)

Abstract

由于对有区分度的区域进行定位和细粒度特征学习的挑战性，细粒度分类任务是困难的。

现有的方法大多是独立解决这些问题，而忽略了两者的相关性。

本文提出了一种新的循环注意卷积神经网络，可以在多尺度上递归地学习对有区分度区域的注意力和基于区域的特征表示，并相互增强。

对每个尺度的学习由一个分类子网络和一个注意提议子网络（APN）组成。APN从完整的图像开始，以先前的预测作为参考，从粗到细迭代生成区域注意力。而较细尺度的网络则从先前尺度提取一个放大的、有向的区域作为输入。

Introduction

细粒度识别的挑战主要有两项，分别是：

1. 有区分度的区域定位；
2. 从这些区域上学习特征。

先前的工作通过引进一些基于局部的检测框架已经获得了一些成功，他们主要包含两个阶段：

1. 通过分析神经网络中得到的卷积响应检测可能的目标区域；
2. 从每个区域提取有区分度的特征并且编码他们为一个压缩的向量来识别。

目前的结果十分可观，进一步的提升也受到很大的限制：

1. 人为定义的局部或者通过务监督的方式学习到的局部不一定对机器分类是有帮助的；
2. 存在于局部中的轻微的视觉差异还是很难去学。本文发现：局部检测和细粒度特征学习是相关的，因此能够强化彼此。

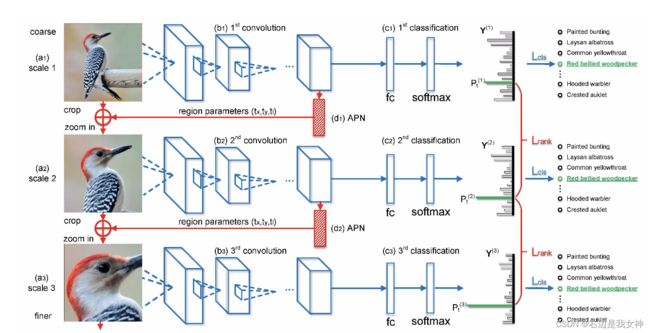
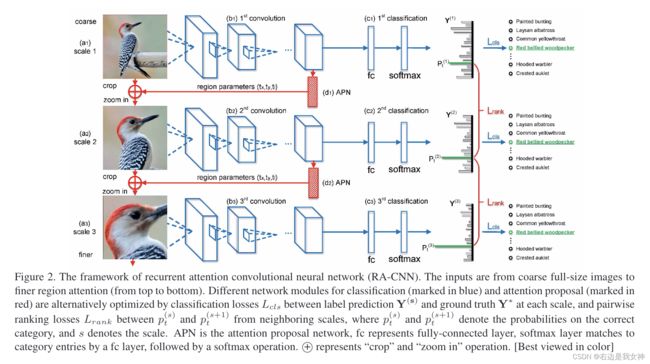
本文提出了一种无边界框/部分注释的方法，是一个循环注意力卷积神经网络（RA-CNN）。

RA-CNN是一个堆叠的网络，它的输入是从整张图像到多尺度的细粒度局部区域。

首先，多尺度网络共享相同的结构但是每一尺度都对应着不同的参数来匹配这个不同分辨率的输入。

不同尺度的学习过程包含了一个分类子网络和一个注意力建议子网络（能够确保每个尺度上足够的辨别能力并为下一个更精细的尺度生成准确的关注区域）。

其次，专门用于高分辨率区域的更精细的尺度网络将简化的关注区域作为输入，以提取更多的细粒度特征。

最后，用了 intra-scale softmax损失来指导分类网络，用了inter-scale pairwise ranking损失来指导注意力提议网络。

Approach

Attention Proposal Network

Multi-task formulation

收到区域建议网络RPN的启发，本文提出了一种注意力建议网络。

给定一张图X，首先提取基于区域的深度特征，表示为$W_c\ast X$。

第一个任务是生成一个概率分布p，可以表示为：$$p(X)=f(W_c\ast X)$$

其中函数f表示为一个全连接层来映射着个卷积特征到一个特征向量以及一个softmax层来进一步转变这个特征向量到概率值。

第二个任务是为下一个更精细的尺度预测关注区域的一组框坐标。通过将关注区域用三个参数近似为一个方形：$$[t_x,t_y,t_l]=g(W_c\ast X)$$
其中，$t_x,t_y$表示方形的中心坐标，$t_l$表示方形的边长。

其中函数g表示为两个堆叠的全连接层。值得一提的是APN的学习是以弱监督的方式训练的。

Attention localization and amplification

一旦假设了关注区域的位置，本文就用更高的分辨率将关注区域裁剪并放大更精细的尺度，以提取更细粒度的特征。

为了确保APN可以在训练中被优化，本文通过提出一个二维的boxcar函数来作为一个注意力掩码来近似裁剪操作。

基于上述表征，裁剪操作能够通过一个原始图像在粗尺度和一个注意力掩模上逐元素相乘来执行，这可以描述为：

其中，

当k很大的时候，可以视为阶跃函数。意思就是x大于0的时候近似为1，小于0的时候近似为0.

这一个思路真的很妙！

boxcar函数有两个优点：

1. 很好地逼近裁剪操作；
2. 在关注区域和box坐标之间建立分析表示。

尽管关注的区域已经被局部化，但有时仍然难以从高度局部化的区域中提取有效的特征表示。因此，我们通过自适应缩放将区域放大到更大的大小。具体来说，本文通过双线性插值来通过线性映射计算$X^{att}$中最近四个输入的放大输出：

Classification and Ranking

图样本的损失函数定义为：

$Y^s$指的是每一尺度的分布向量，$Y^{\ast }$指的是gt。

Lcls是分类损失，主要优化卷积层和分类层的参数。

从成对排序损失得出的$p_t^s$指的是在标签t上的预测可能性，具体而言，这个排序损失可表示为：

这说明了，局部预测的概率值应该高于上一级局部。

总结

本文的整体框架是一个由粗到细的循环神经网络，每一个时间步给出下一步应该输入的图像区域。

其中值得注意的分类细节有：

1. 对每个时间步的输出都做了分类损失的计算并且通过排序损失约束局部预测的精读；
2. 通过boxcar函数近似阶跃函数，给出了可训练的crop策略；
3. 通过插值的手段对精细图像输入进行优化。

Learning Multi-Attention Convolutional Neural Network for Fine-Grained Image Recognition(by localization-classification subnetwork)

Abstract

识别细粒度类别高度依赖于区分部分定位和基于部分的细粒度特征学习。

现有的方法主要是独立地解决这些问题而忽略了部分定位和细粒度特征学习是相互关联的。

本文提出了一种基于多注意卷积神经网络的新型的局部学习方法，使得两者相辅相成。

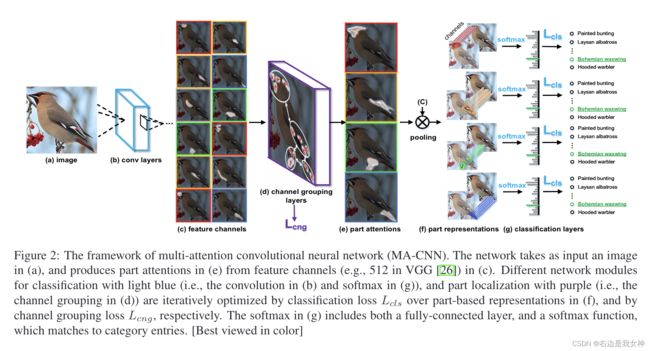
MA-CNN由卷积子网络、通道分组和部分分类子网络组成。通道分组网络将卷积层的输出作为输入特征通道，通过聚类、加权和池化，从空间相关通道件生成多个部分。

部分分类网络进一步按每个单独的部分对图像进行分类，通过它可以学习到更具辨别性的细粒度特征。

本文还提出了两种损失函数来指导通道分组和部分分类。

本文创新点：

1. 利用feature map不同通道（channels）关注的视觉信息不同，峰值响应区域也不同这一特点，聚类响应区域相近的通道，得到 part attentions
2. 本文提出了一个channel grouping loss，目的让part内距离更近（intra-class similarity），不同part距离尽量远（inter-class separability）

Introduction

基于定位-分类的方法的主要问题是依赖手工的局部注释并且这种注释不一定是好的。

目前的解决方法分为两条路子，第一条是直接提取更精细化的特征，第二条是对局部检测进行弱监督的学习。

本文觉得，在没有明确局部约束的情况下，类别级别的CNN的辨别能力眼红限制了部分定位和特征学习的性能（这边指的是第二条路子）。此外，本文发现，局部定位和细粒度特征学习是相互关联的，可以互相加强。

头部定位于促进头部附近的特定模式，然后反过来细化头部定位。

本文提出了一种基于多注意力卷积神经网络的局部学习方法，用于无边界框/局部标注的细粒度学习。

首先，一个卷积特征通道通畅与一个特定的视觉模式是相关的。通道分组子网络由此将空间相关的模式聚类并且加权到局部注意力图。这些图来自于邻近位置出现峰值响应的通道。多样化的高响应位置进一步构成了多个局部注意力图，从中我们能够按照固定的尺寸裁剪得到一些局部提议。

然后，一旦获得了局部提议，局部分类网络就进一步根据局部特征对图像进行分类。这些特征是从全卷积特征图中提取出来的。这样的设计可以消除对其他部分的依赖，特别优化与某部分相关的一组特征通道。

最后，联合实施两个优化损失函数，以指导通道分组和基于局部的分类的多任务学习，这促使MA-CNN从特征通道中生成有区别的部分，并以相互增强的方式从部分中学习到更细粒度的特征。

Approach

1. 整张图送入CNN，提取基于局部的特征表示；
2. 通过通道分组和加权层生成多张局部注意力图（e），随后用sigmoid函数生成概率；
3. 用空间注意力机制对基于局部的特征表示进行池化得到特征（f）；
4. 最后，通过全连接层和softmax层对每一特征进行计算得到概率分数。

我们需要关注的是如何得到局部注意力图以及如何进行池化。

Multi-Attention CNN for Part Localization

虽然一张卷积特征图可以对应某种类型的视觉模式，但是很难仅通过单一通道表示丰富的局部信息。

因此，本文提出了一种通道分组和加权的子网络来对空间相关的细微模式进行聚类以得到紧凑且有区分度的局部。这样一个过程简而言之是从一组通道中找到相邻范围都处于峰值的通道组。

每个通道可以表示为一个位置向量，其元素是所有训练图像实例的峰值相应的坐标，表示为：$$[t_x^1,t_y^1,...,t_x^{\Omega },t_y^{\Omega }]$$

每一对都表示为第i个图像的峰值响应的坐标，Omega是训练集的大小。

我们可以把位置向量作为特征，对不同的通道进行N聚类，来作为N个局部检测器。

为了确保训练时通道分组可以被优化，本文提出了通道分组层来用全连接层还原通道上的排列以近似这种分组。

我们定义一组全连接层$F=[f_1,...,f_N]$，其中每一个函数都将卷积特征作为输入，输出通道的权重。

本文通过两个步骤得到分组结果$d_i(X)$：

1. 预训练（3）式中的参数，这通过结合（2）式进行监督学习；
2. 通过端到端学习来优化。

即预训练+微调的方式。

于是，每一部分的注意力图如下表示：

$[\cdot {]}_j$表示第j个特征图，它表示一个部位注意力图。第i部分的最终特征表示通过每个通道上的空间池化进行计算：

Mi(X)表示值得关注的局部，比如头部区域都是1，其余部位都是0，之后相乘之后头部这块区域的卷积特征就能被完整的取出来。

Multi-task Formulation

Loss function

损失函数定义为：

其中，针对通道的损失函数如下所示：

Dis是距离函数，Div是多样性函数。DIs函数鼓励一个紧凑的分布，其具体形式如下所示：

tx与ty是注意力图上面响应大的坐标，这里的意思就是如果你这个位置响应大，那么就要离这个极值位置近。

Div的目的则是为了获取特征图之间的多样性：

Alternative optimization

本文以一种相互增强的方式来学习。

首先，固定卷积层，通过公式7对图中的d阶段的图进行优化，这部分的目的是为了定位局部。

然后，我们固定通道分组层，用分类损失对图中的b阶段进行学习，目的是进行细粒度特征的学习。

这种学习的过程是迭代的，直到损失函数不再发生变化。

Joint Part-based Feature Representation

我们已经知道每个通道分组都会池化出一个表示局部的特征，于是最终的特征将这些局部以及全局特征connotation得到最终集成的特征（有研究表明这是有益的）。

总结

本文的思路是中规中矩的，有点类似15年那篇end-to-end法的思路之作，以CNN每一通道的意义作为出发点，设计了通道组层，通过池化的手段得到每一部分的特征，从而拼凑出最后的特征。

本文需要注意的有：

1. 依然对分类和局部特征获取设置了对应的损失函数；
2. 值得一提的是，其迭代的训练策略很巧妙。

Low-rank Bilinear Pooling for Fine- Grained Classification(by end-to-end feature encoding)

Abstract

对二阶局部特征统计数据池化来形成一个高维度的双线性特征已经显示了最先进的性能。

为了解决高维度的计算需求，本文提出了将协方差特征表示为矩阵，并应用低秩双线性分类器。

得到的分类器可以不显式地计算双线性特征映射的情况下进行评估，可以大大减少计算时间及所需要学习的有效参数量。

为了进一步压缩模型，我们提出一个分类器进行协同分解，将双线性分类器集合分解为一个公因式和每个类的紧凑项。协同分解的思想可以通过两个卷积层进行部署，并在端到端体系结构中进行训练。

本文还提出了一种简单而有效的初始化方法，避免显式地先训练与分解较大的双线性分类器。

Fine-Grained Recognition as HSnet Search for Informative Image Parts(by localization-classification subnetwork)

Abstract

本文的工作基于这样一个假设：当处理对象类之间的细微差异时，关键是识别并解释是少数有信息的图像部分。因为其余图像上下文不仅可能是无信息的，而且可能会损害识别。

这促使我们将我们的问题描述为在深度卷积神经网络生成的深度特征图上连续搜索信息部分。

这种搜索的一种状态是图像中的提议边界框集，有信息的被H函数拿来验证，并用S函数产生新的候选框。

这两种功能通过LSTM统一到一个新的深度循环结构中，称为HSnet。

因此，HSnet生成信息图像部分的建议，将所有建议融合到最终的细粒度识别。本文根据对部分注释的可用性来指定HSnet的监督和弱监督训练。