机器学习之过拟合和欠拟合
文章目录
- 前言
- 什麽是过拟合和欠拟合?
- 过拟合和欠拟合产生的原因:
-
- 欠拟合(underfitting):
- 过拟合(overfitting):
- 解决欠拟合(高偏差)的方法
-
-
- 1、模型复杂化
- 2、增加更多的特征,使输入数据具有更强的表达能力
- 3、调整参数和超参数
- 4、增加训练数据往往没有用
- 5、降低正则化约束
-
- 解决过拟合(高方差)的方法:
-
-
- 1、增加训练数据数
- 2、使用正则化约束
- 3、减少特征数
- 4、调整参数和超参数
- 5、降低模型的复杂度
- 6、使用Dropout
- 7、提前结束训练
-
- 小例
- 實戰
- 總結
前言
随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容之过拟合和欠拟合。
什麽是过拟合和欠拟合?
- 欠拟合是指模型在训练集、验证集和测试集上均表现不佳的情况;
- 过拟合是指模型在训练集上表现很好,到了验证和测试阶段就很差,即模型的泛化能力很差。
过拟合和欠拟合产生的原因:
欠拟合(underfitting):
- 模型复杂度过低
- 特征量过少
过拟合(overfitting):
- 建模样本选取有误,如样本数量太少,选样方法错误,样本标签错误等,导致选取的样本数据不足以代表预定的分类规则
- 样本噪音干扰过大,使得机器将部分噪音认为是特征从而扰乱了预设的分类规则
- 假设的模型无法合理存在,或者说是假设成立的条件实际并不成立
- 参数太多,模型复杂度过高
- 对于决策树模型,如果我们对于其生长没有合理的限制,其自由生长有可能使节点只包含单纯的事件数据(event)或非事件数据(no event),使其虽然可以完美匹配(拟合)训练数据,但是无法适应其他数据集
- 对于神经网络模型:a)对样本数据可能存在分类决策面不唯一,随着学习的进行,,BP算法使权值可能-收敛过于复杂的决策面;b)权值学习迭代次数足够多(Overtraining),拟合了训练数据中的噪声和训练样例中没有代表性的特征
解决欠拟合(高偏差)的方法
1、模型复杂化
对同一个算法复杂化。例如回归模型添加更多的高次项,增加决策树的深度,增加神经网络的隐藏层数和隐藏单元数等
弃用原来的算法,使用一个更加复杂的算法或模型。例如用神经网络来替代线性回归,用随机森林来代替决策树等
2、增加更多的特征,使输入数据具有更强的表达能力
特征挖掘十分重要,尤其是具有强表达能力的特征,往往可以抵过大量的弱表达能力的特征。
特征的数量往往并非重点,质量才是,总之强特最重要。
能否挖掘出强特,还在于对数据本身以及具体应用场景的深刻理解,往往依赖于经验。
3、调整参数和超参数
超参数包括:
神经网络中:学习率、学习衰减率、隐藏层数、隐藏层的单元数、Adam优化算法中的β1和β2参数、batch_size数值等。
其他算法中:随机森林的树数量,k-means中的cluster数,正则化参数λ等。
4、增加训练数据往往没有用
欠拟合本来就是模型的学习能力不足,增加再多的数据给它训练它也没能力学习好。
5、降低正则化约束
正则化约束是为了防止模型过拟合,如果模型压根不存在过拟合而是欠拟合了,那么就考虑是否降低正则化参数λ或者直接去除正则化项
解决过拟合(高方差)的方法:
1、增加训练数据数
- 发生过拟合最常见的现象就是数据量太少而模型太复杂
- 过拟合是由于模型学习到了数据的一些噪声特征导致,增加训练数据的 量能够减少噪声的影响,让模型更多地学习数据的一般特征
- 增加数据量有时可能不是那么容易,需要花费一定的时间和精力去搜集处理数据
- 利用现有数据进行扩充或许也是一个好办法。例如在图像识别中,如果没有足够的图片训练,可以把已有的图片进行旋转,拉伸,镜像,对称等,这样就可以把数据量扩大好几倍而不需要额外补充数据
- 注意保证训练数据的分布和测试数据的分布要保持一致,二者要是分布完全不同,那模型预测真可谓是对牛弹琴了。
2、使用正则化约束
代价函数后面添加正则化项,可以避免训练出来的参数过大从而使模型过拟合。使用正则化缓解过拟合的手段广泛应用,不论是在线性回归还是在神经网络的梯度下降计算过程中,都应用到了正则化的方法。常用的正则化有l1正则和l2正则,具体使用哪个视具体情况而定,一般l2正则应用比较多。
3、减少特征数
欠拟合需要增加特征数,那么过拟合自然就要减少特征数。去除那些非共性特征,可以提高模型的泛化能力.
4、调整参数和超参数
不论什么情况,调参是必须的
5、降低模型的复杂度
欠拟合要增加模型的复杂度,那么过拟合正好反过来。
6、使用Dropout
这一方法只适用于神经网络中,即按一定的比例去除隐藏层的神经单元,使神经网络的结构简单化。
Dropout是在训练网络时用的一种技巧(trike),相当于在隐藏单元增加了噪声。Dropout 指的是在训练过程中每次按一定的概率(比如50%)随机地“删除”一部分隐藏单元(神经元)。所谓的“删除”不是真正意义上的删除,其实就是将该部分神经元的激活函数设为0(激活函数的输出为0),让这些神经元不计算而已。
7、提前结束训练
即early stopping,在模型迭代训练时候记录训练精度(或损失)和验证精度(或损失),如果模型训练的效果不再提高,比如训练误差一直在降低但是验证误差却不再降低甚至上升,这时候便可以结束模型训练了。
小例
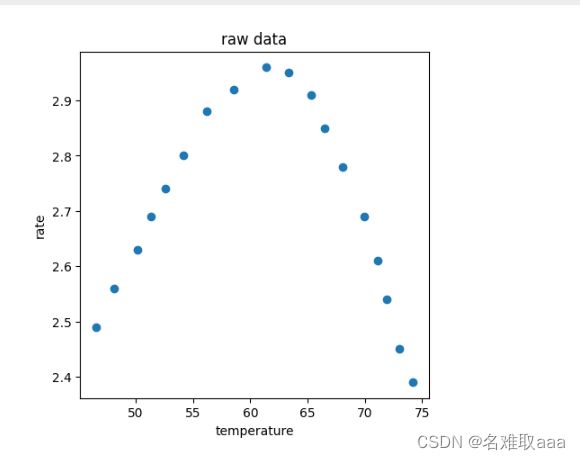
我们知道酶的活性会随温度的变化而变化,在最适温度达到最高,高于或低于最适温度都会有所降低,那么我们若想预测某温度下酶的活性时,该怎么判断模型是否欠拟合或过拟合了呢?来看几幅图

可以看到大概在60度左右酶的活性最高,在这之前和之后都会有所降低,我们预想的模型大概是这样的。它的决策边界可能如图所示。
r = θ₀ + θ₁t + θ₂t²
如果说模型过于简单了,就可能就会得到一条直线。这种训练好后的模型既不能满足训练数据的预期,也不能满足新数据的预期,此时它就是属于欠拟合。(训练数据和新数据的预测结果都不准确)
r = θ₀ + θ₁t
当然,如果模型过于复杂了也不是一件好事。虽然它可以很好的拟合我们的训练数据,但在新数据的预测上就不尽人意了。如下图,对应训练数据,该模型的预测结果是非常准确的,但是我们知道在温度超过最适温度后,酶的活性就会降低,图示结果明显错误,这种情况就是过拟合。(对训练数据的预测结果非常准确,但对新数据的预测结果不准确)

![]()
實戰
酶活性預測實戰task:
- 基於T-R-train.csv數據,建立綫性回歸模型,計算其在T-R-test.csv數據上的r2分數,可視化模型預測結果
- 加入多項式特徵(2次、3次),建立回歸模型
- 計算多項式回歸模型對測試數據進行預測的r2分數,判斷哪個模型預測更準確
- 可視化多項式回歸模型數據預測結果,判斷哪個模型預測更准確
#load the data
import pandas as pd
import numpy as np
data_train = pd.read_csv('T-R-train.csv')
data_train
#define X_train and y_train
X_train = data_train.loc[:,'T']
y_train = data_train.loc[:,'rate']
#visualize the data
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(5,5))
plt.scatter(X_train,y_train)
plt.title('raw data')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()
X_train = np.array(X_train).reshape(-1,1)
轉一下類型不然後面會報下面錯誤
ValueError: Expected 2D array, got 1D array instead:
array=[46.53 48.14 50.15 51.36 52.57 54.18 56.19 58.58 61.37 63.34 65.31 66.47
68.03 69.97 71.13 71.89 73.05 74.21].
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.
#linear regression model prediction
from sklearn.linear_model import LinearRegression
lr1 = LinearRegression()
lr1.fit(X_train,y_train)
#load the test data
data_test = pd.read_csv('T-R-test.csv')
data_test
#define X_test and y_test
X_test = data_test.loc[:,'T']
y_test = data_test.loc[:,'rate']
X_test = np.array(X_test).reshape(-1,1)
#make prediction on the training and testing data
y_train_predict = lr1.predict(X_train)
y_test_predict = lr1.predict(X_test)
from sklearn.metrics import r2_score
r2_train = r2_score(y_train,y_train_predict)
r2_test = r2_score(y_test,y_test_predict)
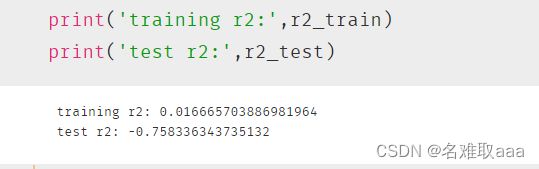
print('training r2:',r2_train)
print('test r2:',r2_test)
可以看出r2_score值很低也就是説明模型很差
#generate new data
X_range = np.linspace(40,90,300).reshape(-1,1)
y_range_predict = lr1.predict(X_range)
fig2 = plt.figure(figsize=(5,5))
plt.plot(X_range,y_range_predict)
plt.scatter(X_train,y_train)
plt.title('prediction data')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()
可視化看一下,可以明顯看出不是一個好的訓練模型,這是個明顯的欠擬合的bad fit
加入多項式特徵(2次、3次),建立回歸模型
#多項式模式
#generate new features
from sklearn.preprocessing import PolynomialFeatures
poly2 = PolynomialFeatures(degree=2) # 二階
X_2_train = poly2.fit_transform(X_train)
X_2_test = poly2.transform(X_test)
poly5 = PolynomialFeatures(degree=5) # 五階
X_5_train = poly5.fit_transform(X_train)
X_5_test = poly5.transform(X_test)
print(X_5_train.shape)
lr2 = LinearRegression()
lr2.fit(X_2_train,y_train)
y_2_train_predict = lr2.predict(X_2_train)
y_2_test_predict = lr2.predict(X_2_test)
r2_2_train = r2_score(y_train,y_2_train_predict)
r2_2_test = r2_score(y_test,y_2_test_predict)
lr5 = LinearRegression()
lr5.fit(X_5_train,y_train)
y_5_train_predict = lr5.predict(X_5_train)
y_5_test_predict = lr5.predict(X_5_test)
r2_5_train = r2_score(y_train,y_5_train_predict)
r2_5_test = r2_score(y_test,y_5_test_predict)
print('training r2_2:',r2_2_train)
print('test r2_2:',r2_2_test)
print('training r2_5:',r2_5_train)
print('test r2_5:',r2_5_test)
看一下r2_score越接近1越好,可以看出多項式的比綫性回歸的效果好的多。同時也可以看出五階對於訓練數據r2分數高(預測準確),但對於預測數據r2分數低(預測不準確)
X_2_range = np.linspace(40,90,300).reshape(-1,1)
X_2_range = poly2.transform(X_2_range)
y_2_range_predict = lr2.predict(X_2_range)
X_5_range = np.linspace(40,90,300).reshape(-1,1)
X_5_range = poly5.transform(X_5_range)
y_5_range_predict = lr5.predict(X_5_range)
fig3 = plt.figure(figsize=(5,5))
plt.plot(X_range,y_2_range_predict)
plt.scatter(X_train,y_train)
plt.scatter(X_test,y_test)
plt.title('polynomial prediction result (2)')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()
可視化二階,看出擬合和預測效果都還不錯,是個good fit
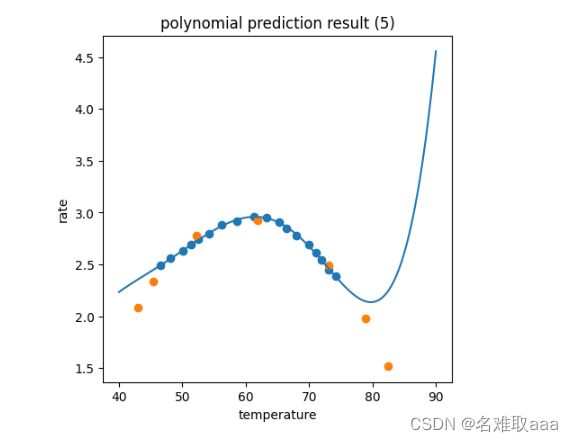
fig4 = plt.figure(figsize=(5,5))
plt.plot(X_range,y_5_range_predict)
plt.scatter(X_train,y_train)
plt.scatter(X_test,y_test)
plt.title('polynomial prediction result (5)')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()
可視化五階,看出擬合很完美但是預測效果不佳,是個過擬合bad fit
總結
酶活性預測實戰summary:
- 通過建立二階多項式回歸模型,對酶活性實現一個較好的預測,無論針對訓練或測試數據都得到一個高的r2分數
- 通過建立綫性回歸、五階多項式回歸模型,發現存在欠擬合或過擬合情況。過擬合情況下,對於訓練數據r2分數高(預測準確),但對於預測數據r2分數低(預測不準確)
- 無論是通過r2分數,或是可視化模型結果,都可以發現二階多項式回歸模型效果最好
這就是本次學習过拟合和欠拟合的筆記
附上本次實戰的數據集和源碼:
鏈接:https://github.com/fbozhang/python/tree/master/jupyter