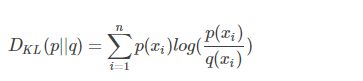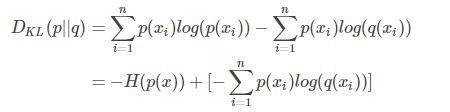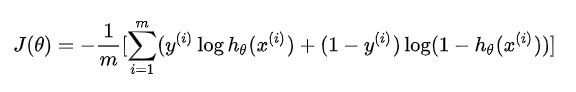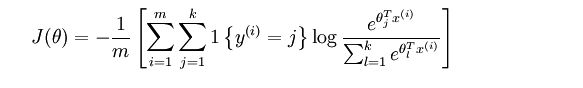惭愧啊,读研的时候学得正是模式识别;当看着书本上都是公式推导、博士师兄们也都在公式推导研究新算法的时候,排斥心理到了顶点,从此弃疗。
工作三年,重新捡起,因为更关注实际操作,所以选择了《python 深度学习》这本书,辅助Andrew Ng视频+博客,希望能够从应用的角度去使用机器学习这门工具,不重蹈覆辙
不想老生常谈,别人讲得很好的,就直接引用了;之前已经了解的概念,也不赘述了; 只关注自己不懂的、以及记录学习过程,所以这会是一个很“草率”的系列...
一、 线性回归
二、logistic 回归与softmax 分类器:
logistic 回归是一个二分类器,softmax 分类器是一个多分类器,它们的激活函数描绘了事件的分布,也就是某事发生的概率(很重要!很重要!很重要!)
对于logistic回归,采用的sigmoid function;可以看到$g(z)$的取值在(0, 1),且大多数情况下趋于1或0,这不正好表示一个二分类问题嘛:某事发生的概率接近于1,或接近于0
softmax 分类器采用了softmax激活函数,假设输出层有$n$个节点,第$i$个节点的softmax 值为
$ S_i = \frac{e^{x_i} } {\sum_{j=1}^n e^{x_j} }$
每个值在[0,1]之间,且所有和为1,是不是多类别事件的概率呢?
损失函数:
损失函数的作用是什么? 描绘一组样本的真实值$y$与预测值$h$之间的差距
对于离散问题,怎么去描绘这个差距呢?这里用的是交叉熵(可参考)
1. 信息量
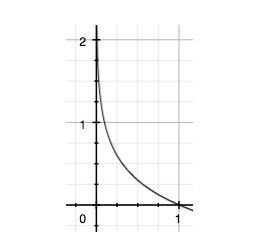
假设事件i发生的概率为$p(x_i)$, 则它包含的信息量为 $-ln(p(x_i))$
如下图所示,$p(x_i)$ 取值为[0, 1],当一件很小概率的事情发生了,给人直觉的冲击越大,它所包含的信息量越大
2. 熵
熵表示对一个问题信息量的期望
假设一个问题有n种可能性,每种可能发生的概率为$p(x_i)$, 则其熵为:
$H(x) = -\sum_{i=1}^n p(x_i)ln(p(x_i))$
3. KL离散度与交叉熵
KL离散度又称为相对熵,它用来衡量两个概率分布之间的差异,KL离散度越小,分布越接近。
假如样本真实属于P分布,机器学习预测为Q分布,那么它们之间的KL离散度为:
可以看到上式第一项 $-H(p(x))$ 是固定值,第二项就是交叉熵。当交叉熵越小,KL离散度越小,预测分布就越接近于真实分布
所以在logistic回归和softmax分类器中,均使用交叉熵来作为损失函数。对于二分类问题,n=2, 交叉熵又叫作二元交叉熵,其等价为:
$-(p(x_i)ln(q(x_i)) + (1-p(x_i))ln((1-q(x_i))))$
因此,logistic回归损失函数:
softmax分类器损失函数:
三、梯度下降算法
1. 梯度下降的直观理解
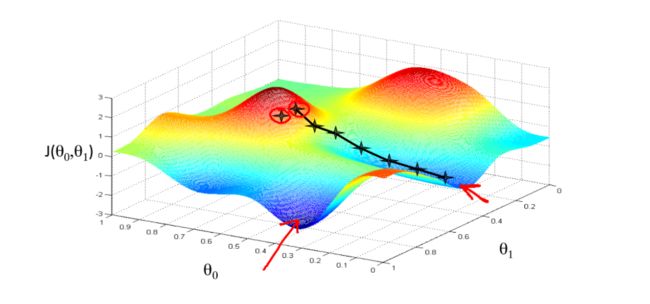
想象你在山上的某一点,要以最快的速度下山。 学习率相当于步长,偏导数相当于方向,偏导数越接近于0,越接近一个局部最小点。
初始位置选择不一样,到达的局部最优值也不同
梯度下降算法中权重的初始值可以采用统一初始值,但扩展到反向传播算法却需要随机初始化权重
2. 学习率对梯度下降收敛的影响
3. Normalization Input 有利于梯度下降算法的收敛
其实吧,在Andrew Ng的视频中,归一化、标准化的英文翻译都是Normalization...有时标准化也翻译成standardization,用于以Normalization区分
归一化:
1.Max-min归一化
$x_i = \frac{x_i-x_{min}}{x_{max}-x_{min}}$
2.Mean归一化
$x_i = \frac{x_i-x_\mu}{x_{max}-x_{min}}$
标准化:
1. Z-Score 标准化
$x_i = \frac{x_i-x_\mu}{\sigma}$
其中 $\mu$是样本数据的均值(mean),$\sigma$是样本数据的标准差(std)
什么时候用归一化,什么时候用标准化? sorry,网上的博客没看懂...
四、反向传播算法
可以参考这篇推导过程,关键是用到了链式法则;平常都是用封装好的API,也就略过这部分了
反向传播算法中参数需要随机初始化
1. 一般取值在[-ε, +ε],ε 是一个任意给定的很小的数
什么给很小的数呢?这样$z=\theta^Tx$ 也会是一个在0附近很小的数;对于sigmoid, tanh 等激活函数,z在0附近曲线不那么平缓,收敛速度更快
2. 如果初始化采用统一初始值,隐藏层的输出是相等的,梯度下降更新后,连接相同出发点的权重值是一样的
继续梯度下降更新,连接相同出发点的权重值永远是一样的,隐藏层的表示也相等,从而网络变得冗余,拟合效果也不好