基于遗传算法实现多式联运问题
基于遗传算法实现多式联运问题
- 前言
- 算法简介
-
- 遗传算法
- 多式联运
- 遗传算法进行求解
-
- 编码
- 适应度函数评价:
- 选择,交叉和变异
- 结果分析
- 写在最后
前言
本次博客主要分享我之前看过了一个问题,叫做“多式联运”问题,主要是为了方便我练习使用遗传算法,虽然现在matlab官方提供其工具箱,但是从底层上去理解和编写一次遗传算法有助于我之后的提升,加之之前对相位板的优化过程中使用到遗传算法,但是自己又不是很熟悉,一直想着好好去解决这个问题,同时呢看到这样的问题,所以自己就尝试去是用遗传算法去解决它,效果很好。
算法简介
遗传算法
对于遗传算法的说明和介绍,我觉得我不用直接去叙述了,如果有需要的话,我后面再加上更加详细的介绍,这里我推荐一位博主的介绍吧:
链接: 遗传算法详解(GA)(个人觉得很形象,很适合初学者).
多式联运
多式联运问题的介绍可以看一下这个链接:
链接:多式联运
上面的链接是百度百科里面对多式联运问题的介绍,很详细,只是我个人对这个不是很感冒,我看到的是一篇论文的介绍。下面我们开始对论文开始一个简单的叙述和介绍:

引言
多式联运的主要影响因素

问题的描述和假设
假设有一批物件以集装箱为单位需从 A 城市运往 B 城市, 有若干节点, 在整个运输过程中采用了由公路运输、 铁路运输、 水路运输组成的多式联运的运输方式。 在整个线路规划中, 充分考虑到降低物流企业的投入成本、 提升运输效率、 提高客户满 意度, 从而得到基于多方面因素的多式联运路径优化方案。
现在存在两种情况,第一种-是物件从A城市运往B城市的过程中不能在相同的城市中的节点进行逗留,简单的来说,从A出发的货物,必须的下一节点是B城市里面的接受点,同样的,到达B城市的货物下一次要直接返回A城市里面的节点,同一个城市内部没有交通运输方式;第二种就是同一个城市内部是可以有运输方式的,这里两种方式的计算方法都一样,就是在编码的过程中存在细微的差别。
对于不同的问题,我们需要进行的不同的假设条件和模型建立,这个我就直接以第一种的方式进行说明,具体的模型建立我这里就不在去赘述了,详细的打开可以自己去知网上寻找相关的文章或者自己建立(之前其他的博客自己写的公式总是会出现问题,所以我也就不在去添加公式了)
遗传算法进行求解
编码
遗传算法的第一步就是对问题的目标解进行编码,编码的方式有“二进制编码”,“十进制编码”,“格雷码”等等情况,我们首先假设A城市中的节点个数,例如"1~ 10",B城市中的节点个数为"11~18",多式联运问题中我们选择三种交通方式,即**“公路”,“水路”和“铁路”**,三种方式分别用“1”,“2”,“3”代表,问题中我们直接采用十进制进行编码操作。
编码思想:
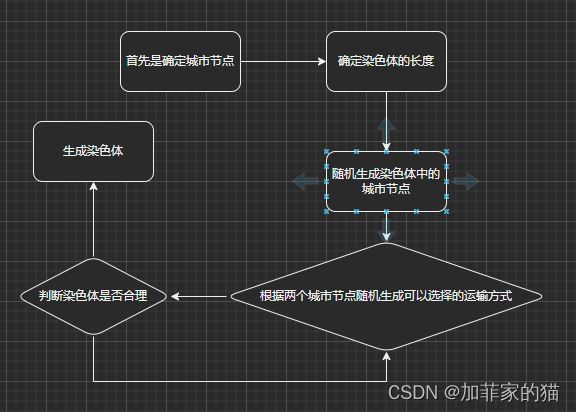
%% ===================子函数================================================
% 用于产生计算种群的大小
function population = popocreat(popsize,N,icity,jcity)
% popsize表示种群的大小
% N表示城市节点的个数
% icity表示初始城市
% jcity表示目标到达的城市
% 其中奇数为表示城市的节点,偶数位表示输运的方式
global RailDisdata WaterDisdata
H = 1:12; %城市节点的数量以及标签
A = H(1:5);
B = H(6:12); % 表示两个省中城市的标签
test=500;
Initialpop = zeros(test,2*N-1);
Initialpop(:,1) = icity;
Initialpop(:,2*N-1) = jcity; % 基因首尾位置
% 可以途径的城市的节点的标签
if icity<5
id1=A==icity;
A(id1) = [];
id2=B==jcity;
B(id2) = [];
else
id1=B==icity;
B(id1)=[];
id2=A==jcity;
A(id2)=[];
end
% 可以选择的城市节点的个数
sizeA= size(A,2);
sizeB= size(B,2);
适应度函数评价:
选择,交叉和变异

在这里进行一个简单的说明,对于选择操作,不一定非得需要使用轮盘赌的方式,其他的方式也是可以的,比如使用“精英选择保留”,"竞标赛“等等
function [newpop] = selection(population,Fitvalue)
% 函数说明:子函数用于计算子代的种群
EliteInvidualrate = 0.1; % 精英个体保留率
Titleracerate = 1-EliteInvidualrate; %锦标竞赛保留
poplen = size(population,1); %种群的个数
Titlenumber = fix(poplen*Titleracerate);
Elitenumber = ceil(poplen*EliteInvidualrate);
function scro = crossover(population,pcrossover)
% 函数说明:
% 此子函数用于计算交叉操作
% 采用双点交叉的原则
%% ====================================
% 首先确定交叉的次数
poplen = size(population,1);
chromosomelen = size(population,2); %染色体的长度
function snnew = mutation(population,pmutation,icity,jcity)
% 函数说明:
% 此子函数用于计算说明染色体的变异操作
poplen = size(population,1);
chromosomelen = size(population,2); %染色体的长度
% 产生随机概率
poprand = rand(poplen,1);
结果分析
使用上面的遗传算法,自己判定相关的数据,比如交叉概率,变异概率,或者使用自适应变异和交叉等,都可以,此外适应度函数的设计也需要进行一个简单操作,最后的迭代结果为
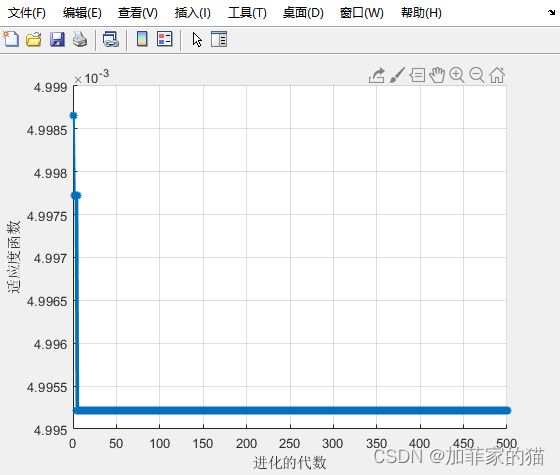
在进化500代之后,可以得到比较合适的结果。
写在最后
关于这篇博客,里面的遗传算法是自己编写的,可能存在相关的不当之处,所以的代码的全部没有贴出来,有需要的可以联系我。
主要参考文献:


