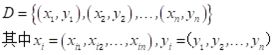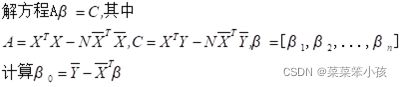机器学习之线性回归（matlab）

目录

一、基本概念

二、概念的数学形式表达

三、确定w和b

1.读取或输入数据

2.归一化、标准化

2.1 均值

2.2 归一化

2.3 标准化

3.求解w和b

1.直接解方程

2.最小二乘法（least square method）求解：

4. 评估回归模型

四、regress线性回归命令

1.调函数解方程

2.对原始值和预测值进行绘图

3. 画残差图：

五、matlab颜色表

六、matlab调色板

1、常用颜色的RGB值

2、产生标准调色板的函数

---

一、基本概念

线性(linear)：

指量与量之间按比例、成直线的关系，在空间和时间上代表规则和光滑的运动，一阶导数为常数

非线性(non-linear)：

指不按比例、不成直线的关系，代表不规则的运动和突变，一阶导数不为常数。

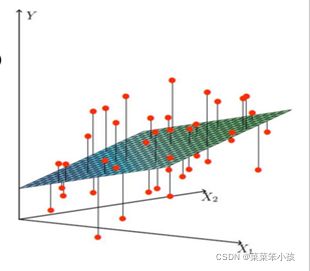
一个线性的例子：

数据：工资和年龄（2个特征）

目标：预测银行会贷款给我多少钱（标签）

考虑：工资和年龄都会影响最终银行贷款的结果，那么他们各自有多大的影响呢？（参数）

通俗的解释：

x1,x2就是我们的两个特征（年龄、工资），y是银行最终会借给我们多少钱

找到最合适的一条线（想象一个高维）来最好的拟合我们的数据点

数学形式来了

二、概念的数学形式表达

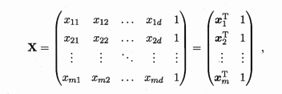
给定数据集：

数据的矩阵形式：

 线性模型(linear model)试图学得一个通过属性组合的线性组合来进行预测的函数，即

用向量形式写成:   

线性回归(linear regression)试图学得一个线性模型以尽可能准确地预测实值输出标记

三、确定w和b

对离散属性：

若属性间存在“序”关系，可通过连续化将其转化为连续值。

若属性间不存在“序”关系，则转化为k维向量。

1.读取或输入数据

matlab不需要导入库，直接引用函数 csvread 读取csv数据文件

首先我们先看看csv数据的导入

% 引用函数 csvread 读取csv数据文件

data = csvread('路径',1,0) #从第二行，第0列读取数据

 读取数据后得分出和为X，何为Y

# matlab从1开始算，与实际一样
X = data[:,1:4]  # 1到4列所有的数据也就是实际的1到4列
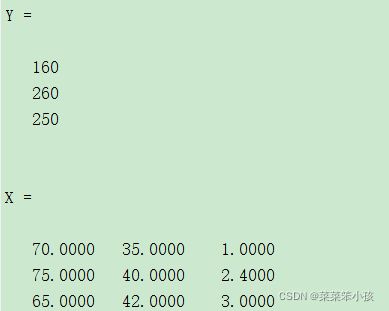
Y = data[:, 6]  # 第6列所有的数据也就是实际的第6列

 接下来我们看看自己建立矩阵的数据读取方式

Y=[160
   260
   250];

X=[70,35,1
 75,40,2.4
 65,42,3];

返回：

 

  说到矩阵了，就顺便说一下

创建矩阵的相关知识：

(1) ones()函数：产生全为1的矩阵，ones(n)：产生n*n维的全1矩阵，ones(m,n)：产生m*n维的全1矩阵；
(2) zeros()函数：产生全为0的矩阵；
(3) rand()函数：产生在（0，1）区间均匀分布的随机阵；
(4) eye()函数：产生单位阵；
(5) randn()函数：产生均值为0，方差为1的标准正态分布随机矩阵。

2.归一化、标准化

2.1 均值

# MATLAB直接引用mean()函数就好
X_mean = mean(X)
Y_mean = mean(Y)

1. mean:计算向量均值。mean(x,1)列向量均值,mean(x,2)行向量均值。  mean2(x)矩阵均值.

2. std：计算向量均方差，std(x,0,1)列向量均方差,std(x,0,2)行向量均方差。 std2(x)矩阵均方差

3. var：计算向量方差，var(x)

4. sse：误差平方和,sse(x)。越接近于0，说明拟合的越好，数据预测越成功。

5. mse：均方差平方和,mse(x)=sse(x)/N。意义同sse

6. R-square：确定系数。确定系数是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好。

要想确定w和b，首先要视情况决定是否需要对数据进行归一化或标准化

2.2 归一化

%归一化

X=[70,35,1
 75,40,2.4
 65,42,3];
for X=X
    MappedX = (X-min(X))/(max(X)-min(X))
end

%用函数mapminmax
%默认的map范围是[-1, 1]，所以如果需要[0, 1]，则按这样的格式提供参数:

MappedData = mapminmax(OriginalData, 0, 1);

% 只按行归一化，如果是矩阵，则每行各自归一化，如果需要对整个矩阵归一化

FlattenedData = OriginalData(:)'; % 展开矩阵为一列，然后转置为一行。
MappedFlattened = mapminmax(FlattenedData, 0, 1); % 归一化。

% 还原为原始矩阵形式。此处不需转置回去，因为reshape恰好是按列重新排序
MappedData = reshape(MappedFlattened, size(OriginalData)); 

2.3 标准化

% z-score 标准化
% 新数据=（原数据-均值）/标准差
% 标准化以后，X中元素的取值范围为实数。

X=zscore(X)

3.求解w和b

1.直接解方程

N = length(Y);

A = X'*X-(N*X_mean'*X_mean);
C=X'*Y - (N*X_mean'*Y_mean);
B = (A^-1*C).'

2.最小二乘法（least square method）求解：

把数据集D表示为一个m*(d+1)大小的矩阵X，其中每行对应于一个示例，改行前d个元素对应于示例的d个属性值，最好一个元素恒置为1，即

A=[1 2 3;4 5 6;7 8 9];
B = ones(3,1) %生成3行1列的1矩阵
% B=[1;1;1];  %一共三行，用“;”分开
A_column=[A B];
display(A_column);%输出结果

当X^TX 为满秩矩阵(full-rank matrix) 或正走矩阵(positive definite matrix) 时，令

得到

w = (X'*X)^-1*X'*Y %变量的系数
w0 = Y_mean - X_mean*w %常数

 其中(X^TX)^-l是矩阵(X^TX)的逆矩阵.令xi = (xi ,l) ,则最终学得的多元线性回归模型为

YY = X*w+w0 %Y的估计值

4. 评估回归模型

%离差平方和
S = var(Y);
fprintf('离差平方和S=：%d\n',S)
%回归平方和
U = var(YY);
fprintf('回归平方和U=：%d\n',U)
%剩余平方和
Q=S-U;
fprintf('剩余平方和Q=：%d\n',Q)
%复可决系数
R2 = U/S;
fprintf('复可决系数R2=：%d\n',R2)
%负相关系数
R = sqrt(U/S);
fprintf('复相关系数R=：%d\n',R)
%回归均方
% n= X_mean 的个数
UU = U/n;
fprintf('回归均方=：%d\n',UU)
%剩余均方
% N= Y的个数
QQ = Q/(N-n-1);
fprintf('剩余均方=：%d\n',QQ)
%剩余标准差
s = sqrt(QQ);
fprintf('剩余标准差s=：%d\n',s)
%方程显著性检验值
F = UU/QQ;
fprintf('方差显著性检验值F=：%d\n',F)

四、regress线性回归命令

用于一元及多元线性回归，本质上是最小二乘法。在Matlab 2014a中，输入help regress ，会弹出和regress的相关信息

调用格式：

• B = regress(Y,X)
• [B,BINT] = regress(Y,X)
• [B,BINT,R] = regress(Y,X)
• [B,BINT,R,RINT] = regress(Y,X)
• B,BINT,R,RINT,STATS] = regress(Y,X)
• [...] = regress(Y,X,ALPHA)

参数解释：

• B：回归系数，是个向量（“the vector B of regression coefficients in the  linear model Y = X*B”）。
• BINT：回归系数的区间估计（“a matrix BINT of 95% confidence intervals for B”）。
• R：残差（ “a vector R of residuals”）。
• RINT：置信区间（“a matrix RINT of intervals that can be used to diagnose outliers”）。
• STATS：用于检验回归模型的统计量。有4个数值：判定系数R^2，F统计量观测值，检验的p的值，误差方差的估计。
• ALPHA：显著性水平（缺少时为默认值0.05）。

1.调函数解方程

% 方程求解函数使用
[b,bint,r,rint,stats] = regress(Y,X);

2.对原始值和预测值进行绘图

x = 1:1:N;
plot(x,Y,'-*b',x,YY,'-or'); %线性，颜色，标记

% hold on; %表示在同一张图上继续作画
% title('x'); %命名标题
% axis([0 1 0 10]) % 设置坐标轴在指定的区间
% xlabel('t'); %命名x轴
% ylabel('x'); %命名y轴
% grid on %显示坐标轴网格线
% legend('Y','YY'); %*加标注，2条线分别代表是什么*

3. 画残差图：

figure %创建窗口
rcoolot(r,rint) %绘制残差图

五、matlab颜色表

线型	说明	标记符	说明	颜色	说明
-	实线(默认)	+	加号符	r	红色
--	双划线	o	空心圆	g	绿色
:	虚线	*	星号	b	蓝色
:.	点划线	.	实心圆	c	青绿色
		x	叉号符	m	洋红色
		s(square)	正方形	y	黄色
		d	菱形	k	黑色
		^	上三角形	w	白色
		v	下三角形
		>	右三角形
		<	左三角形
		p(pentagram)	五角星
		h(hexagram)	六边形
		square	正方形
		pentagram	五角形
		hexagram	六角形

六、matlab调色板

1、常用颜色的RGB值

  --------------------------------------------

    颜色   R   G   B     颜色   R   G  B

  --------------------------------------------

     黑    0   0  1     洋红    1  0   1

     白    1   1  1     青蓝    0  1   1

     红    1   0  0     天蓝 0.67 0   1

     绿    0   1  0     橘黄    1 0.50

     蓝    0   0  1     深红   0.5 0  0

     黄    1   1  0      灰    0.5 0.50.5      

  --------------------------------------------

⚠️注意：MATLAB中调色板色彩强度[0,1]，0代表最暗，1代表最亮。

2、产生标准调色板的函数

  -------------------------------------------------

    函数名      调色板

  -------------------------------------------------

     Hsv     色彩饱和度，以红色开始，并以红色结束

     Hot     黑色－红色－黄色－白色

     Cool    青蓝和洋红的色度

     Pink     粉红的色度

     Gray     线型灰度

     Bone    带蓝色的灰度

     Jet      Hsv的一种变形，以蓝色开始，以蓝色结束

     Copper   线型铜色度

     Prim     三棱镜，交替为红、橘黄、黄、绿和天蓝

     Flag     交替为红、白、蓝和黑

--------------------------------------------------

缺省情况下，调用上述函数灰产生一个64×3的调色板，用户也可指定调色板大小。